泛函分析 01.04 距离空间-闭集、可分性、列紧性

§1.3闭集、可分性、列紧性 

1.3.1距离空间的闭集 

内容:闭集的定义及性质. 
(1)利用开集研究闭集; 
(2)从点集结构上研究闭集. 

定义1.3.1设X是一个距离空间,集合A⊂X称为是闭的, 
若它的补集A c =X∖A是开的. 
定理1.3.2.设X是一个距离空间,则B ¯ ¯ ¯  (x 0 ,r)={x∈X|d(x,x 0 )≤r} 
和S(x 0 ,r)={x∈X|d(x,x 0 )=r}是闭集. 
分析:根据闭集的定义,只要证明它们的补集是开集即可,用开集定义来证明. 
证明:(1)设y∈B ¯ ¯ ¯  (x 0 ,r) c ,要证y是B ¯ ¯ ¯  (x 0 ,r) c 的内点. 

∵d(y,x 0 )=α>r. 
令β=α−r>0,对于∀z∈B(y,β),有 
d(x 0 ,z)≥d(y,x 0 )−d(y,z) 
=α−d(y,z) 
>α−β=r. 
故B(y,β)⊂B ¯ ¯ ¯  (x 0 ,r) c . 
即B ¯ ¯ ¯  (x 0 ,r) c 是开的,于是B ¯ ¯ ¯  (x 0 ,r)是闭的. 
(2)由S(x 0 ,r) c =B(x 0 ,r)∪B ¯ ¯ ¯  (x 0 ,r) c 是开的 
(根据任意多个开集的并集是开集), 
因此S(x 0 ,r)是闭集. 
记F为距离空间(X,d)中全体闭集.利用关于补集的DeMorgan公式, 
结合定理(开集的性质,决定空间拓扑结构的三条性质),得 
定理1.3.3设(X,d)是一个距离空间,则 
(1)全空间与空集是闭集; 
(2)任意多个闭集的交是闭集; 
(3)有限多个闭集的并是闭集. 

1.3.2闭集的结构 

闭集的结构相对比较复杂,这从Cantor集是闭集可以反映出来. 
下面从点集的结构上进一步研究闭集. 
定义1.3.4设X是一个距离空间,A⊂X,x∈X.如果对于∀ε>0, 
球B(x,ε)中都包含A中的点,即 
B(x,ε)∩A≠∅(∀ε>0),(1.3.1) 
则称x为A的接触点. 
注:A中的点一定是A的接触点,A的接触点可能属于A也可能不属于A. 

定义1.3.5设X是一个距离空间,A⊂X,x∈X.如果对于∀x>0, 
球B(x,ε)中都包含A中不同于x的点,即 
B(x,ε)∩(A∖{x})≠∅(∀ε>0),(1.3.2) 
则称x为A的聚点. 
注:聚点一定是接触点,反过来不一定. 

例1.3.6a点和b点是开区间(a,b)的聚点(也是接触点),但不属于开区间(a,b), 
闭区间[a,b]的聚点全部在[a,b]中. 

例1.3.7设A=[0,1]∩{2},2是A的接触点,但不是A的聚点. 

例1.3.8设X=C[0,T],A={x(t)|x(0)=0,且|x(t)|<1(0≤t≤T)}. 

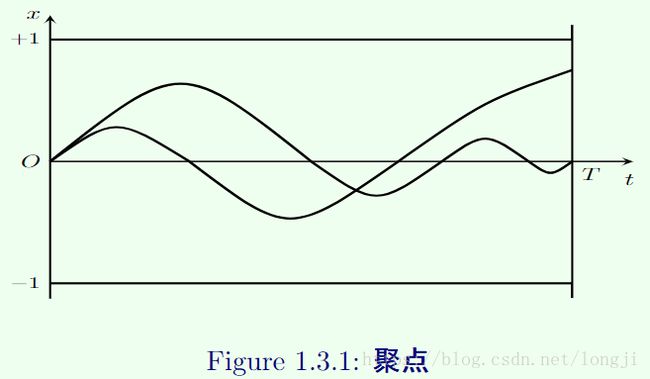
我们注意到x 0 (t)≡1不是A的接触点. 
因为对于所有的x∈A,d(x 0 ,x)≥1. 
如果对于∀x>0,球B(x,ε)中都包含A中的点,即 
B(x,ε)∩A≠∅(∀ε>0), 
则称x为A的接触点. 
如果对于∀ε>0,球B(x,ε)中都包含A中(不同于x)的点,即 
B(x,ε)∩A≠∅(B(x,ε)∩A∖{x}≠∅)(∀ε>0), 
则称x为A的接触点(聚点). 

例1.3.9设X表示由[0,T]上全体连续函数组成的集合,距离定义为: 
d 2 (x,y)={∫ T 0 |x(t)−y(t)| 2 dt} 12  , 
A={x(t)|x(0)=0,且|x(t)|<1(0≤t≤T)}, 

则可以证明x 0 ≡1是A的接触点(也是A的聚点). 
注:一个点是否是一个集合的接触点和空间的距离有关. 

用接触点来定义闭集. 
定义1.3.10设X是一个距离空间,A⊂X,A的接触点的全体为A的闭包,记为A ¯ ¯ ¯  . 
注:∵A中的点一定是A的接触点,∴A⊂A ¯ ¯ ¯  . 
定理1.3.11设X是一个距离空间,A⊂X,A是闭集当且仅当A=A ¯ ¯ ¯  . 
证明:“⇐”“由A=A ¯ ¯ ¯  ⇒A是闭集”. 
只要证明A c 是开的. 
令x∈A c ,由A=A ¯ ¯ ¯  ,x不是A的接触点(定义1.3.4). 
∴存在ε 0 >0,使得B(x,ε 0 )∩A=∅, 
∴B(x,ε 0 )⊂A c .因此A c 是开的,即A是闭集. 
“⇐”“A是闭集⇒A=A ¯ ¯ ¯  ”. 
由于A⊂A ¯ ¯ ¯  ,只需证明A ¯ ¯ ¯  ⊂A. 
令x∈A ¯ ¯ ¯  ,假若x∈ ¯ ¯  A,即 
x属于开集A c (这是由于A是闭集), 
于是存在ε 0 >0,B(x,ε 0 )⊂A c ,即:B(x,ε 0 )∩A=∅, 
这和x∈A ¯ ¯ ¯  矛盾. 
注意:证明过程中用到了接触点、开集、闭集、闭包的定义. 

定理1.3.12设X是一个距离空间,A⊂X,A是闭集当且仅当A中收敛点列 
{x n }⊂A的极限属于A. 
注:闭集可以理解为:在闭集里极限运算是封闭的. 
证明:“⇒”设A是闭的,且{x n }⊂A收敛, 
lim n→∞ x n =x 0 ,要证明x 0 ∈A. 
由x 0 =lim n→∞ x n ,可知: 
对于∀ε>0,都有x n (n充分大)满足d(x n ,x 0 )<ε, 
即x n ∈B(x 0 ,ε).这表明x 0 是A的接触点. 
∴x 0 ∈A ¯ ¯ ¯  . 
由A是闭集,即：A=A ¯ ¯ ¯  ,所以x 0 ∈A. 
“⇐”假定每个收敛点列的极限都属于A,要证A是闭集. 
根据定理1.3.11,只要证明A=A ¯ ¯ ¯  ,即由x 0 ∈A ¯ ¯ ¯  推出x 0 ∈A. 
令x 0 ∈A ¯ ¯ ¯  ,根据闭包的定义(全体接触点,定义1.3.4), 
对于∀n∈N,在B(x 0 ,1n )∩A中至少存在一点x n . 
显然lim n→∞ x n =x 0 , 
由已知,得x 0 ∈A,因此A是闭的. 

定理1.3.13(点到集合的距离)设X是一个距离空间,A⊂X,x∈X,称 
d(x,A)=inf{d(x,ω)|ω∈A}(1.3.3) 
为点x到集合A的距离. 
注:由定理1.3.11、1.3.12可以证明 
A ¯ ¯ ¯  ={x|d(x,A)=0},(1.3.4) 
且A ¯ ¯ ¯  是包含A的最小闭集. 

1.3.3可分的距离空间 

实数空间中,有理数是稠密的,有理数是可数的, 
任何一个实数都可以用有理数列来逼近. 
我们希望把这样的性质“类比”地推广到一般的空间中. 
重点：稠密集，由其定义可分距离空间；判定稠密性、距离空间的可分性. 

定义1.3.14(稠密集)设A，B是距离空间X中的点集,如果B ¯ ¯ ¯  ⊃A, 
则称B在A中稠密. 
ε−δ语言描述(闭包、接触点的定义1.3.4): 
∀x∈A,∵x∈B ¯ ¯ ¯  ,∴∀ε>0,B(x,ε)∩B≠∅, 
即存在y∈B,使得d(x,y)<ε. 
也就是说A中的每一点都可以用B中的点来逼近: 
∀x∈A,∀ε>0,∃y∈B,s.t.d(x,y)<ε(1.3.5) 
注意:定义并没有要求B⊂A. 

例1.3.15A=[0,1],B是[0,1]中全体有理数.B ¯ ¯ ¯  =[0,1],B ¯ ¯ ¯  ⊃A. 
所以B在A中稠密,这里B⊂A且B≠A. 

例1.3.16如果A是[0,1]中全体无理数,B是[0,1]中全体有理数,我们有B ¯ ¯ ¯  ⊃A, 
即B在A中稠密,但是B∩A=∅. 

定义1.3.17(可分距离空间)设X是距离空间,如果X中存在一个可数稠密子集, 
则称X是可分的. 
对于子集A⊂X,如果X中存在可数子集B,使得B在A中稠密,则称A是可分的. 
由稠密的定义以及(1.3.5)式有: 
命题1.3.18距离空间(X,d)是可分的当且仅当存在一个具有下列性质的 
可数集{x n }: 
∀x∈X和∀ε>0,至少存在一个x k ∈{x n },s.t.d(x k ,x)<ε. 
注:可分空间中的任意一点可通过一个可数集来近似逼近. 
并且对于∀ε>0,⋃ k=1 ∞ B(x k ,ε)=X. 

例1.3.19R n 是可分的. 
R n 中的有理点(各个坐标都是有理数)是可数集,且在R n 中稠密. 

例1.3.20C[a,b]是可分的. 
分析：只要找到C[a,b]中的可数稠密子集{x n (t)}即可. 
由命题1.3.18，找到的{x n (t)}应满足: 
对于∀x(t)∈C[a,b]和∀ε>0,至少存在一个x n (t),使得d(x n ,x)<ε. 
证明思路:连续函数用多项式逼近,多项式用有理多项式逼近, 
全体有理系数多项式是C[a,b]中的可数子集,所以C[a,b]可分. 
证明(1)由Weierstrass逼近定理,对于 
∀x(t)∈C[a,b],存在多项式P n (t)一致收敛到x(t). 
(证明参阅P.M.Fitzpatrick:《AdavncedCalculus》p.188) 
即对于∀x(t)∈C[a,b],∀ε>0,存在 
P n (t)=a 0 +a 1 t+⋯+a n t n . 
其中a i ∈R(i=1,2,⋯,n),使得 
|P n (t)−x(t)|<ε(∀t∈[a,b]). 
(2)而P n (t)又可以用P r n (t)一致逼近, 
这里P r n (t)=r 0 +r 1 t+⋯+r n t n ,其中r 0 ,⋯,r n 是有理数. 
∵{P r n (t)}是可数的,∴C[a,b]是可分的. 

例1.3.21l ∞ 是不可分的. 
分析:用反证法来证明. 
证明(1)l ∞ ={全体有界的实数列}. 
x={ξ k },y={η k }∈l ∞ ,(1.3.6) 
d(x,y)=sup k |ξ k −η k |.(1.3.7) 
d(x,y)是l ∞ 上的一个距离. 

(2)设x={ξ k },其中ξ k =0,或1.这样的x的全体记为A. 
A的势是连续统(二进制小数对应[0,1]上全体实数). 
∀x,y∈A,x≠y,则d(x,y)=sup k |ξ k −η k |=1. 
(3)假若l ∞ 可分,则存在可数的稠密子集E, 
对于∀x∈E,作开球B(x,13 ),则l ∞ ⊂⋃ x∈E B(x,13 ),