游戏开发之从零开始了解渲染管线【下】- 图形绘制管线及简易实现

1 基本流程

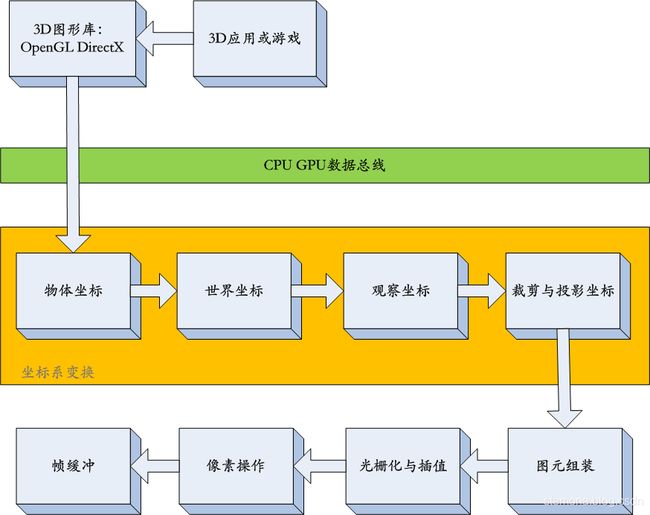
• 定义：图形绘制管线描述GPU渲染流程，即“给定视点、三维物体、光源、照明模式，和纹理等元素，如何绘制一幅二维图像”

• 阶段：应用程序阶段、几何阶段、光栅阶段

  • 应用程序阶段：使用高级编程语言进行开发，主要和CPU、内存打交道，诸如碰撞检测、场景图建立、空间八叉树更新、视锥裁剪等经典算法都在此阶段执行。在该阶段的末端，几何体数据，包括顶点坐标、法向量、纹理坐标、纹理等，通过数据总线传送到图形硬件;

  • 几何阶段：主要负责顶点坐标变换、光照、裁剪、投影以及屏幕映射，该阶段基于GPU进行运算，在该阶段的末端得到了经过变换和投影之后的顶点坐标、颜色、以及纹理坐标

  • 光栅阶段：基于几何阶段的输出数据，为像素（Pixel）正确配色，以便绘制完整图像，该阶段进行的都是单个像素的操作，每个像素的信息存储在颜色缓冲器（color buffer或者frame buffer）中。

光照计算属于几何阶段，因为光照计算涉及视点、光源和物体的世界坐标，所以通常放在世界坐标系中进行计算；而雾化以及涉及物体透明度的计算属于光栅化阶段，上述两种计算都需要
值信息（Z值），而深度值是在几何阶段中计算，并传递到光栅阶段。

• 总体GPU流程：物体坐标 - 世界坐标 - 观察坐标 - 裁剪与投影坐标 - 基元组装 - 光栅化与插值 - 像素操作 - 帧缓冲，如图。

  

以上流程涉及以下空间转换：

物体空间->世界空间->观察空间->裁剪空间（->设备归一化（NDC）空间）->屏幕空间

详细可参见数学基础章节及参考文献[2]的第7章节，或参考链接（《空间变换》)

• 概念梳理：

  • 图元组装：就是将顶点以一定的顺序组装成三角形。

  • 帧缓冲（Frame Buffer)：是用一个视频输出设备从包含完整的帧数据的一个内存缓冲区中来驱动一个视频显示设备。在内存缓冲区中标准上包含了屏幕上每个像素的色彩值组成。色彩值通常存储成1比特位(黑白色彩),4比特位调色版,8比特位调色版,16比特位高色彩,24比特位真色彩格式，与一个额外的alpha通道来保存像素透明度信息。

  • 纹理坐标（UV坐标）：U和V分别是图片在显示器水平、垂直方向上的坐标，取值一般都是0~1，水平方向的第U个像素/图片宽度，垂直方向的第V个像素/图片高度。

  • CCV（标准观察体，Canonical View Volume）： CVV是一个正方体，x, y, z的范围都是[-1，1]，多边形裁剪就是用该规则体完成。

2 各阶段实现

2.1 几何阶段

空间转换主要通过矩阵运算完成，各变换矩阵详见第1节数学基础。

物体空间->世界空间->观察空间->裁剪空间（->设备归一化（NDC）空间）->屏幕空间

所需用用到的矩阵分别是世界矩阵、观察矩阵及投影矩阵，在1.3节中有详细介绍。

几何阶段还需要进行图元装配，也就是将顶点以一定的顺序组装成三角形，可使用了顶点索引的方式来组织顶点数据，若进行背面消隐，则各面的顶点存储顺序必须一致（按顺时针或逆时针组织顶点数据，并约定法向量的方向）。

2.2 光栅化阶段

光栅化通过插值把一个图元过滤成能够在屏幕上表示它的一系列离散的片元，是把顶点数据转换为片元的过程，具有将图转化为一个个栅格组成的图像的作用，特点是每个元素对应帧缓冲区中的一像素。简单的说，显示器给定了有限个像素组成的矩阵，光栅化就是将顶点数据转化至每个矩阵中的像素点进行显示。

光栅化的本质为坐标变换与几何离散化，如图。

2.2.1 直线光栅化

在数学上，理想的直线是没有宽度的、由无数个点构成的集合。当我们对直线进行光栅化时，只能在显示器所给定的有限个像素组成的矩阵中，确定最佳逼近该直线的一组像素，并且按扫描线顺序对这些像素进行写操作，直线光栅化一般为以下三种算法：

• 数值微分DDA（Digital Differential Analyzer）算法

• 中点画线算法

• Bresenham算法

以上三种算法中，Bresenham算法的效率较高。详细介绍可参考：从零开始写光栅化渲染器2：直线绘制光栅化算法与Bresenham快速画线算法

直线光栅化一般用于显示图形线框，若要实现顶点色模式或纹理模式则需要用到三角形光栅化与区域填充。

2.2.2 三角形光栅化与区域填充

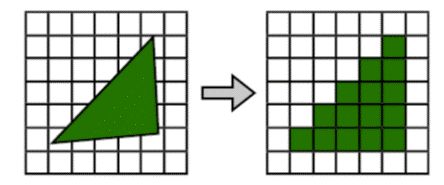
光栅化三角形的原理很简单，就是在三角形内部画线填充（区域填充），如图所示。

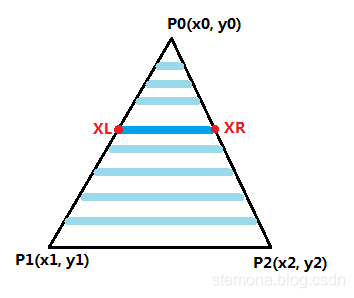
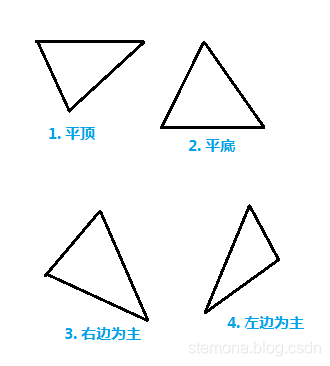
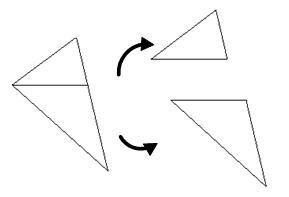
光栅化基本上都是基于对多边形进行扫描线转换，把一个三角形的三个顶点所包围的区域转换成和屏幕水平方向平行的由像素组成的一条条扫描线。

常用的方法是将三角形统一按平顶与平底三角形来处理，如图。

详细分析可参考：深入探索透视纹理（上）与三角形光栅化算法

区域填充即给出一个区域的边界，要求对边界范围内的所有像素单元赋予指定的颜色代码，区域填充中最常用的是多边形填色。可以采用扫描线填充算法实现，可采用上一节所提直线光栅化算法实现。

2.2.3 纹理映射

光栅化过程当中，需要对纹理坐标进行透视校正插值，不能简单的采用投影平面上的坐标进行仿射线性映射，因为投影平面上的线性关系，并不适用于原来三维空间。

[外链图片转存失败(img-sF9zzxyQ-1565165127889)(UvProjection.png)]

纹理坐标是定义在红色的多边形上的，因此纹理坐标的增量应该是和红色线段的步长对应，若直接在投影平面上线性插值，则是把纹理坐标增量按照蓝色线段的步长平均分配，显然会导致错误。

先明确一下目标
：纹理映射的目标在于得到投影平面上正确插值后的纹理坐标(s’，t’)

这里需要回顾一下投影变换的推导过程，若p的坐标为（x, y, z），纹理坐标为(s,t)，p’ 是p投影之后的点，坐标为(x’, y’, z’)，纹理坐标为(s’,t’)，则有：

x'与y'分别都与1/z线性相关，且x'、y'和s/z、t/z也是线性关系，因此在投影面上应该通过x’和y’对1/z进行线性插值可得到1/z',

然后对s/z、t/z关于x'、y'进行插值得到s'/z'、t'/z'，然后用s'/z’和t'/z'分别除以1/z'，就得到了插值s'和t'。

事实上，就是纹理映射需要用上深度信息，否则纹理显示会出现扭曲。

可以通过一段伪代码来解释这一过程：

//投影平面上扫描线左端点坐标为(lx,ly,lz),纹理坐标为(lu,lv);
//右端点为（rx,ry,rz), 纹理坐标为(ru,rv);扫描线上任意点为(x,y)
factor = (x-lx)/(rx-lx); //同一水平线上
z' = factor*lz + (1-factor)*rz;
uz' = factor*lu + (1-factor)*ru;
vz' = factor*lv + (1-factor)*rv;
u' = uz' / z'; //插值后的纹理坐标
v' = vz' / z';	

以上伪码中(u’,v’)即为映射后的纹理坐标，详细推导可参考：深入探索透视纹理（上）与深入探索透视纹理（下）

为了保证缩放后的纹理不出现严重失真的情况，需要对纹理进行采样，一般有以下几种纹理采样方法：

• 点采样：

  方式一：直接对插值后的纹理坐标直接进行取整操作。

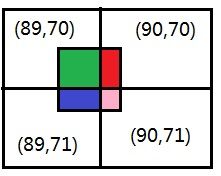
    例：纹理图的尺寸是128*128 ; 插值计算后的某个像素点的纹理坐标为(0,70,0.55)
    纹理坐标进行变化：0.70 * 128 = 89.6，  0.55 * 128 = 70.4
    取整操作得到最后的纹理图上的坐标：(89, 70)
  

  方式二：由于截取了小数部分，所以失去的部分信息，一种稍微改进点的方法就是保留小数部分，而将采取纹理图中相邻的两个像素的值，使用小数部分作为权值来进行采样。

    例：沿用上面数据，取小数部分对相邻像素进行采样：
    0.6 * Texel(89,70) + 0.4 * Texel(90, 70)
  

• 双线性采样：

  对坐标相邻的四个像素进行采样，按权重分配。
  

    各个像素权值推导：
      (89,70) : (89.6 - 89) * (70.4 - 70) = 0.6 * 0.4 = 0.24 ;
      (90,70) : (90 - 86.6) * (70.4 - 70) = 0.4 * 0.4 = 0.16 ;
      (89,71) : (89.6 - 89) * (71 - 70.4) = 0.6 * 0.6 = 0.36 ;
      (90,71) : (90 - 89.6) * (71 - 70.4) = 0.4 * 0.6 = 0.24 ;
    权值之和：0.24 + 0.16 + 0.36 + 0.24 = 1.0
  

  双线性采样方式应用较为广泛。

• 三线性纹理滤波采样

  概念：Mipmap链 的思路就是构建一套纹理，总共需要大约1.3倍的内存，每块子纹理是通过对父纹理过滤而得到，长和宽都是其父纹理的1/2，其面积为父纹理的1/4。 如加载的是一个128*128的纹理图，那么会创建一套64*64， 32*32， 16*16， 8*8， 4*4 ， 2*2， 1*1的纹理图，选取与缩放尺寸最接近的纹理图进行采样，可大大提高效率与效果。

  三线性采样是双线性采样与Mipmap技术的结合，在Mipmap的目标纹理（两张）做双线性插值的同时，还对这两张相邻的纹理按距离再做一次插值。即算出较大的一块纹理上的某点双线性插值像素值和较小的一块纹理上的某点双线性插值像素值，再按目标同两块纹理的距离做一次类似的插值。

  备注：同前两种方式相比，三线性插值的运算量非常大，目前只能依靠硬件来实现。

三种采样详细说明可参博文：DirectX (9) 纹理映射，该文章写的比较简单易懂，另外还可参考纹理映射的双线性插值滤波。

2.2.4 遮挡剔除

遮挡剔除即Occlusion Culling（简称OC），主流引擎中都能看到，其作用在于消耗一小部分CPU资源来消除不可见的物体，不改变最终渲染的画面的同时，降低 GPU 的负载。

这里给出遮挡剔除的一些参考，后面单独介绍遮挡剔除。

• 图形学遮挡剔除算法综述

• 遮挡剔除的低端解决方案

• 合用的遮挡剔除技术

比较流行的方案是Z-Buffer算法，基本思路如下：

（1）存储每个顶点的深度值Z;

（2）每次将像素点颜色写入Frame Buffer时，把该点的Z值也写入Z-Buffer;

（3）每次将像素点颜色写入Frame Buffer之前，如果该位置已经被写入过，将当前Z值与正准备写的点的Z值比较一下，Z值越小（深度值），离屏幕越近，则替换写入。

其优缺点都比较明显：

• 优点：简单与高效

• 缺点：

  • 增加了内存空间，每个顶点都要存储Z

  • 受限于Z的量级 / 精确度

  • 过度渲染，每个像素点可能会写入多次

  • 不支持透明度

3 软渲染管线实现

基于以上基础，可以手撸一个软渲染器，这里就不给出具体源码实现了，源码可参考（看源码更易理解以上所提的概念与流程）：

• 软渲染器的C语言实现

• 软渲染器的C#语言实现

参考文献

[1] 3D数学基础：图形与游戏开发

[2] 计算机图形学（第三版 ）

[3] GPU图形绘制管线

[4] 用C#实现一个简易的软件光栅化渲染器

备注

完整版迁移至：游戏开发之从零开始了解渲染管线