Pytorch实现LSTM和GRU
为了解决传统RNN无法长时依赖问题,RNN的两个变体LSTM和GRU被引入。
LSTM
Long Short Term Memory,称为长短期记忆网络,意思就是长的短时记忆,其解决的仍然是短时记忆问题,这种短时记忆比较长,能一定程度上解决长时依赖。
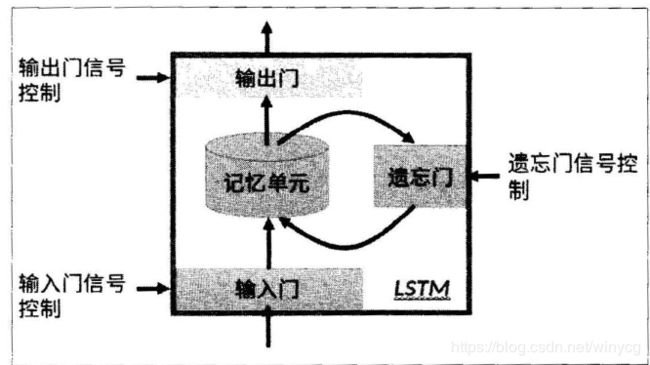
上图为LSTM的抽象结构,LSTM由3个门来控制,分别是输入门、遗忘门和输出门。输入门控制网络的输入,遗忘门控制着记忆单元,输出门控制着网络的输出。最为重要的就是遗忘门,可以决定哪些记忆被保留,由于遗忘门的作用,使得LSTM具有长时记忆的功能。对于给定的任务,遗忘门能够自主学习保留多少之前的记忆,网络能够自主学习。
具体看LSTM单元的内部结构:

 将t-1时刻的网络输出 h t − 1 h_{t-1} ht−1和当前输入的 x t x_{t} xt线性变换后相加结合起来,再经过sigmoid激活函数将结果映射到(0,1)作为衰减系数,视为 C t − 1 C_{t-1} Ct−1记忆的衰减系数,记作 f t f_{t} ft,称为遗忘门:
将t-1时刻的网络输出 h t − 1 h_{t-1} ht−1和当前输入的 x t x_{t} xt线性变换后相加结合起来,再经过sigmoid激活函数将结果映射到(0,1)作为衰减系数,视为 C t − 1 C_{t-1} Ct−1记忆的衰减系数,记作 f t f_{t} ft,称为遗忘门:
f t = σ ( W i f x t + b i f + W h f h t − 1 + b h f ) f_{t}=\sigma(W_{if}x_{t}+b_{if}+W_{hf}h_{t-1}+b_{hf}) ft=σ(Wifxt+bif+Whfht−1+bhf)

i t i_{t} it与 f t f_{t} ft的计算方式类似,作为当前记忆的衰减系数,称为输入门:
i t = σ ( W i i x t + b i i + W h i h t − 1 + b h i ) i_{t}=\sigma(W_{ii}x_{t}+b_{ii}+W_{hi}h_{t-1}+b_{hi}) it=σ(Wiixt+bii+Whiht−1+bhi)
当前时刻 t t t学习到的状态为 C t ~ \tilde{C_{t}} Ct~
C t ~ = tanh ( W i g x t + b i g + W h g h t − 1 + b h g ) \tilde{C_{t}}=\tanh(W_{ig}x_{t}+b_{ig}+W_{hg}h_{t-1}+b_{hg}) Ct~=tanh(Wigxt+big+Whght−1+bhg)
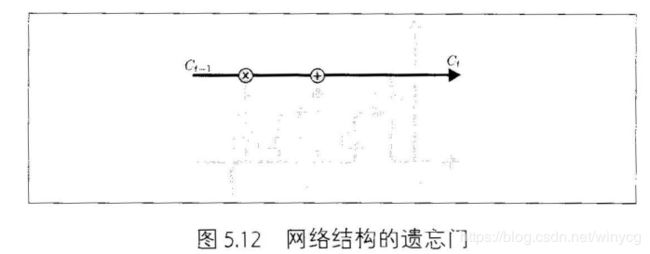
真正输出的状态 C t C_{t} Ct为 C t − 1 C_{t-1} Ct−1和 C t ~ \tilde{C_{t}} Ct~的衰减之和:
C t = f t C t − 1 + i t C t ~ C_{t}=f_{t}C_{t-1}+i_{t}\tilde{C_{t}} Ct=ftCt−1+itCt~
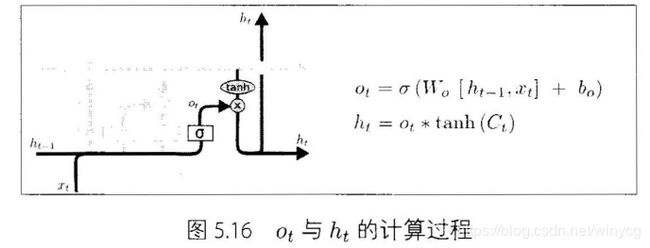
o t o_{t} ot可作为输出门的记忆衰减系数,称为输出门::
o t = σ ( W i o x t + b i o + W h o h t − 1 + b h o ) o_{t}=\sigma(W_{io}x_{t}+b_{io}+W_{ho}h_{t-1}+b_{ho}) ot=σ(Wioxt+bio+Whoht−1+bho)
计算网络输出 h t h_{t} ht:
h t = o t ∗ tanh ( C t ) h_{t}=o_{t}*\tanh(C_{t}) ht=ot∗tanh(Ct)
在每篇文章中,作者都会使用和标准LSTM稍微不同的版本,针对特定的任务,特定的网络结构往往表现更好。
GRU
GRU是Gated Recurrent Unit的缩写,与LSTM最大的不同之处在于GRU将遗忘门和输入门合成一个“更新门”,同时网络不再额外给出记忆状态 C t C_{t} Ct,而是将输出结果 h t h_{t} ht作为记忆状态不断向后传递,网络的输入和输出都简化。
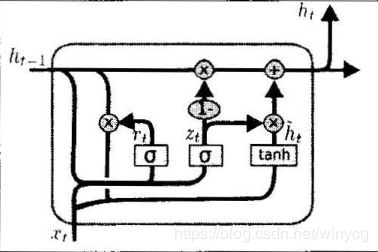
U p d a t e G a t e : z t = σ ( W z h h t − 1 + W z x x t ) R e s e t G a t e : r t = σ ( W r h h t − 1 + W r x x t ) h t ~ = tanh ( W h h ( r t ∗ h t − 1 ) + W h x x t ) h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h t ~ Update\ Gate:z_{t}=\sigma(W_{zh}h_{t-1}+W_{zx}x_{t})\\ Reset\ Gate:r_{t}=\sigma(W_{rh}h_{t-1}+W_{rx}x_{t})\\ \tilde{h_{t}}=\tanh(W_{hh}(r_{t}* h_{t-1})+W_{hx}x_{t})\\ h_{t}=(1-z_{t})*h_{t-1}+z_{t}*\tilde{h_{t}} Update Gate:zt=σ(Wzhht−1+Wzxxt)Reset Gate:rt=σ(Wrhht−1+Wrxxt)ht~=tanh(Whh(rt∗ht−1)+Whxxt)ht=(1−zt)∗ht−1+zt∗ht~
上述的过程的线性变换没有使用偏置。隐藏状态参数不再是标准RNN的4倍,而是3倍,也就是GRU的参数要比LSTM的参数量要少,但是性能差不多。
Pytorch
在Pytorch中使用nn.LSTM()可调用,参数和RNN的参数相同。具体介绍LSTM的输入和输出:
输入: input, (h_0, c_0)
- input:输入数据with维度(seq_len,batch,input_size)
- h_0:维度为(num_layers*num_directions,batch,hidden_size),在batch中的
初始的隐藏状态. - c_0:初始的单元状态,维度与h_0相同
输出:output, (h_n, c_n)
- output:维度为(seq_len, batch, num_directions * hidden_size)。
- h_n:最后时刻的输出隐藏状态,维度为 (num_layers * num_directions, batch, hidden_size)
- c_n:最后时刻的输出单元状态,维度与h_n相同。
LSTM的变量:
- LSTM.weight_ih_l[k]:表示第 k k k层 ( W i i , W i f , W i g , W i o ) (W_{ii},W_{if},W_{ig},W_{io}) (Wii,Wif,Wig,Wio)的input-hidden权重。如果k=0,表示第0层维度为(4*hidden_size, input_size),其他层的维度为(4 * hidden_size, num_directions * hidden_size),接收第k−1层传来的hidden特征。
- LSTM.weight_hh_l[k]: 表示第 k k k层 ( W h i , W h f , W h g , W h o ) (W_{hi},W_{hf},W_{hg},W_{ho}) (Whi,Whf,Whg,Who)的hidden-hidden权重。维度为(4*hidden_size, hidden_size)
- LSTM.bias_ih_l[k]:对应偏置,(4*hidden_size)
- LSTM.bias_hh_l[k]:对应偏置,(4*hidden_size)
以MNIST分类为例实现LSTM分类
MNIST图片大小为28×28,可以将每张图片看做是长为28的序列,序列中每个元素的特征维度为28。将最后输出的隐藏状态 h T h_{T} hT作为抽象的隐藏特征输入到全连接层进行分类。最后输出的
导入头文件:
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
from torchvision import transforms
class Rnn(nn.Module):
def __init__(self, in_dim, hidden_dim, n_layer, n_classes):
super(Rnn, self).__init__()
self.n_layer = n_layer
self.hidden_dim = hidden_dim
self.lstm = nn.LSTM(in_dim, hidden_dim, n_layer, batch_first=True)
self.classifier = nn.Linear(hidden_dim, n_classes)
def forward(self, x):
out, (h_n, c_n) = self.lstm(x)
# 此时可以从out中获得最终输出的状态h
# x = out[:, -1, :]
x = h_n[-1, :, :]
x = self.classifier(x)
return x
训练和测试代码:
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5]),
])
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=128, shuffle=True)
testset = torchvision.datasets.MNIST(root='./data', train=False, download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=100, shuffle=False)
net = Rnn(28, 10, 2, 10)
net = net.to('cpu')
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
# Training
def train(epoch):
print('\nEpoch: %d' % epoch)
net.train()
train_loss = 0
correct = 0
total = 0
for batch_idx, (inputs, targets) in enumerate(trainloader):
inputs, targets = inputs.to('cpu'), targets.to('cpu')
optimizer.zero_grad()
outputs = net(torch.squeeze(inputs, 1))
loss = criterion(outputs, targets)
loss.backward()
optimizer.step()
train_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
print(batch_idx, len(trainloader), 'Loss: %.3f | Acc: %.3f%% (%d/%d)'
% (train_loss/(batch_idx+1), 100.*correct/total, correct, total))
def test(epoch):
global best_acc
net.eval()
test_loss = 0
correct = 0
total = 0
with torch.no_grad():
for batch_idx, (inputs, targets) in enumerate(testloader):
inputs, targets = inputs.to('cpu'), targets.to('cpu')
outputs = net(torch.squeeze(inputs, 1))
loss = criterion(outputs, targets)
test_loss += loss.item()
_, predicted = outputs.max(1)
total += targets.size(0)
correct += predicted.eq(targets).sum().item()
print(batch_idx, len(testloader), 'Loss: %.3f | Acc: %.3f%% (%d/%d)'
% (test_loss/(batch_idx+1), 100.*correct/total, correct, total))
for epoch in range(200):
train(epoch)
test(epoch)