二次曲面、空间曲线的拟合---mathematica

代码

If[Length[Names["Global`*"]] > 0, Remove["Global`*"]];
r[t_] = {
     Cos[t], Sin[t], t};
sample = Table[r[i], {
     i, 0, 2 \[Pi], 0.1}];
xdata = (sample // Transpose)[[1]];
ydata = (sample // Transpose)[[2]];
zdata = (sample // Transpose)[[3]];
xbasis = {
     0.1, Cos[t]};
ybasis = {
     0.1, Sin[t]};
zbasis = {
     0.1, t};
tmp = Table[i, {
     i, 0, 2 \[Pi], 0.1}];
Ax = Map[Function[t, {
     0.1, Cos[t]}], tmp];
Ay = Map[Function[t, {
     0.1, Sin[t]}], tmp];
Az = Map[Function[t, {
     0.1, t}], tmp];
x1 = LinearSolve[Transpose[Ax].Ax, Transpose[Ax].xdata].xbasis;
y1 = LinearSolve[Transpose[Ay].Ay, Transpose[Ay].ydata].ybasis;
z1 = LinearSolve[Transpose[Az].Az, Transpose[Az].zdata].zbasis;
fitfunction = {
     x1, y1, z1};
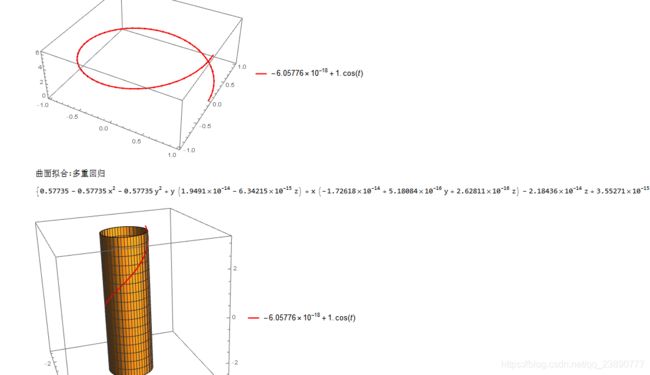
Show[ListPointPlot3D[sample, PlotStyle -> Black], 
 ParametricPlot3D[fitfunction, {
     t, 0, 2 \[Pi]}, PlotStyle -> Red, 
  PlotTheme -> "Detailed"], ImageSize -> Medium]
"曲面拟合:多重回归"
surfacesample = Take[Transpose[sample], 3] // Transpose;
surfacebasis = {
     x^2, y^2, z^2, x*y, x*z, y*z, x, y, z, 1};
Asur = Function[{
     x, y, z}, {
     x^2, y^2, z^2, x*y, x*z, y*z, x, y, z, 
     1}] @@@ surfacesample;
(*LinearSolve[Transpose[Asur].Asur,Transpose[Asur].zdata]*)
fun = NullSpace[Asur].surfacebasis // Simplify
Show[ContourPlot3D[
  fun == 0, {
     x, -\[Pi], \[Pi]}, {
     y, -\[Pi], \[Pi]}, {
     z, -\[Pi], \
\[Pi]}], ParametricPlot3D[fitfunction, {
     t, 0, 2 \[Pi]}, 
  PlotStyle -> Red, PlotTheme -> "Detailed"]]