连分数
对于连分数,我们可以表示为:
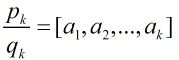
对于无理数,ai一定是无穷数列,反之,对于有理数,ai一定是有穷数列。
对于上式中的p与q,有递推式:

而对于sqrt(n)来说,ai中的首项为一个单独的整数,除了它后面的都会循环。
下面我们来分析一个关于连分数的题目。
题意:给两个整数n和k,n<=10^6,k<=10^9,sqrt(n)可以表示为连分数,求满足数列到ak的结果。
分子分母对1000000007取余。
对于这个问题,当然是先求出数列ai,求这个直接倒啊倒。
关键是有了这个ai数列,如何求到第k位的结果。这个当然有循环节,然后在一个循环节内是可以先处理出结果。
然后再计算有多少个这样的循环节,这部分就可以快速幂,剩下的部分就直接multi暴力吧。
此过程中还有一个重要的点,就是:
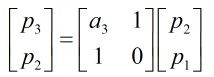
怎么处理的?
在本题由于sqrt(n)的整数部分没有存进a数组,我们知道p1=a1,p2=a1a2+1,所以我们把上述矩阵表示为:
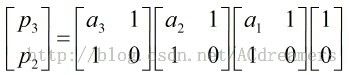
所以这样完全就解决问题了,如果是q,最后面那个矩阵应该是0,1
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>
#include <math.h>
using namespace std;
typedef long long LL;
const int N=50005;
const double eps=1e-8;
const LL MOD=1000000007;
LL a[N];
LL cnt;
struct Matrix
{
LL m[2][2];
};
Matrix per={1,0,0,1};
Matrix multi(Matrix a,Matrix b)
{
int i,j,k;
Matrix c;
for(i=0;i<2;i++)
{
for(j=0;j<2;j++)
{
c.m[i][j]=0;
for(k=0;k<2;k++)
c.m[i][j]+=a.m[i][k]%MOD*b.m[k][j]%MOD;
c.m[i][j]%=MOD;
}
}
return c;
}
Matrix matrix_mod(Matrix a,LL k)
{
Matrix p=a,ans=per;
while(k)
{
if(k&1)
{
ans=multi(ans,p);
k--;
}
k>>=1;
p=multi(p,p);
}
return ans;
}
LL gcd(LL a,LL b)
{
return b? gcd(b,a%b):a;
}
void Loop(LL n)
{
double k=sqrt(n*1.0);
LL q=1,p=(LL)k,tmp=1;
double first=k-p;
while(1)
{
tmp=q;
q=n-p*p;
LL G=gcd(tmp,q);
q/=G;tmp/=G;
k=(sqrt(1.0*n)+p)*tmp/q;
a[cnt++]=(LL)k;
p=abs(p-a[cnt-1]*q);
if(fabs(k-a[cnt-1]-first)<eps) break;
}
}
int main()
{
LL n,k,p,q,x,y;
Matrix ans1,ans2,ans3,A;
while(cin>>n>>k)
{
k++;
cnt=0;
Loop(n);
ans1=ans2=per;
A.m[0][1]=1;
A.m[1][0]=1;
A.m[1][1]=0;
for(int i=cnt-1;i>=0;i--)
{
A.m[0][0]=a[i];
ans1=multi(ans1,A);
}
x=k%cnt;
y=k/cnt;
ans1=matrix_mod(ans1,y);
for(int i=x-1;i>=0;i--)
{
A.m[0][0]=a[i];
ans2=multi(ans2,A);
}
ans3=multi(ans2,ans1);
p=ans3.m[1][0]%MOD;
q=ans3.m[1][1]%MOD;
LL tmp=q; q=p;
p=((LL)sqrt(n*1.0)%MOD*p%MOD+tmp)%MOD;
cout<<p<<"/"<<q<<endl;
}
return 0;
}