图论中的概念(1)——子图、商图与补图
1.子图(subgraph)
设G=(V, E)和G¢=(V¢, E¢)是两个(有向的或无向的)图。
(1) 若V¢ÍV且E¢Í E,则称G¢为G的子图;
(2) 若V¢ÌV且 E¢Ì E,则称G¢为G的真子图(proper-);
(3) 若V¢=V且E¢Í E,则称G¢为G的生成子图(spanning-);
(4)当V¢=V且E¢=E ,或 V¢=V且E¢=Æ时,称G¢为G的平凡子图(trivial-);即,图G 本身和G的零图是G的平凡子图。
2.商图(quotient graph)
设G = (V,E)是一(有向的或无向的) 图,RÍV´V是一结点集V上的等价关系。
那么, 定义图G关于等价关系R的商图为简单图
GR = (VR, ER) 其中:
VR=V/ R={[v]RïvÎV}是V关于等价关系R的商集;
ER ={([u]R, [v]R)ï[u]R ÎVRÙ[v]RÎVRÙ($u¢Î[u]R)($v¢Î[v]R) ((u¢,v¢)ÎE)} 。
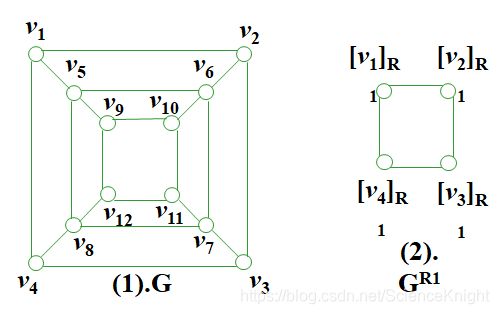
例题.图G如(1)图所示;
其关于等价关系R1 (以划分{ { v1, v5, v9},{ v2, v6, v10},{ v3, v7, v11},{ v4, v8, v12}}给出)的商图GR1如(2)图所示;
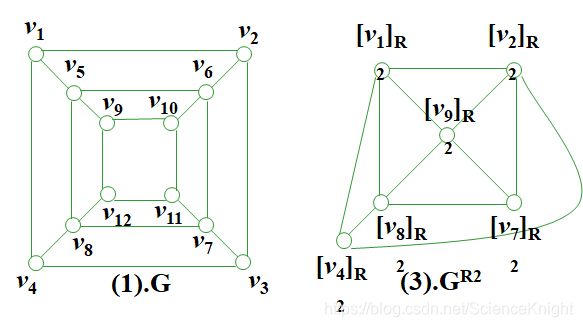
关于等价关系R2 (以划分{ { v1, v5},{ v2, v3, v6},{ v4}, { v7}, { v8},{ v9, v10 , v11, v12}}给出)的商图GR2如(3)图所示;
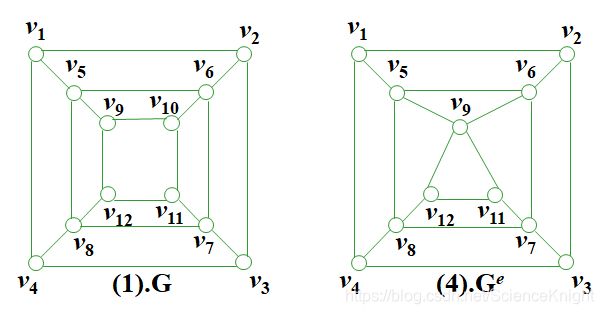
关于等价关系R3 (以划分{ { v1},{ v2},{ v3},{ v4},{ v5}, { v6},
{ v7},{ v8},{ v9, v10},{ v1},{ v12}}给出)的商图GR3如(4)图所示(称为由一条边e=(v9, v10)所导出的商图,记为Ge);
3.补图(complement graph)
设G = (V,E)为一简单图,G* = (V,E*)是与图G相应的完全图。 定义图G的补图 = (V, ) ,其中:
= E* \E。