4.Eigen Tensor详解【三】
目录
七 相关API说明
6.降维运算
7.扫描操作
8 .卷积操作
9.几何运算
(1) reshape(const Dimensions& new_dims)
(2) shuffle(const Shuffle& shuffle)
(3) stride(const Strides& strides)
(4) slice(const StartIndices& offsets, const Sizes& extents)
(5) chip(const Index offset, const Index dim)
(6)reverse(const ReverseDimensions& reverse)
七 相关API说明
6.降维运算
降维运算返回的tensor比原始tensor具有更少的维度,返回的tensor的值是通过对原始tensor的值切片应用一个降维算子来计算的。切片的维度可以手动指定(切片指的是需要获取元素的下标)
所有的降维操作都采用一个类型为
如下代码所示
void testReduction()
{
// Create a tensor of 2 dimensions
Eigen::Tensor a(2, 3);
a.setValues({ {1, 2, 3}, {6, 5, 4} });
//
Eigen::array dims = { 1 }; //沿着第二个维度降维
Eigen::array dims2 = { 0 }; //沿着第一个维度降维
// maximum 返回的是某个维度的最大值
Eigen::Tensor b = a.maximum(dims);
cout << "a" << endl << a << endl << endl;
cout << "b" << endl << b << endl << endl;
Eigen::Tensor c = a.maximum(dims2);
cout << "c" << endl << c << endl << endl;
} 下面沿着两个维度降维
void testReduction2()
{
Eigen::Tensor a(2, 3, 4);
a.setValues({ {
{0.0f, 1.0f, 2.0f, 3.0f},
{7.0f, 6.0f, 5.0f, 4.0f},
{8.0f, 9.0f, 10.0f, 11.0f}},
{
{12.0f, 13.0f, 14.0f, 15.0f},
{19.0f, 18.0f, 17.0f, 16.0f},
{20.0f, 21.0f, 22.0f, 23.0f}} });
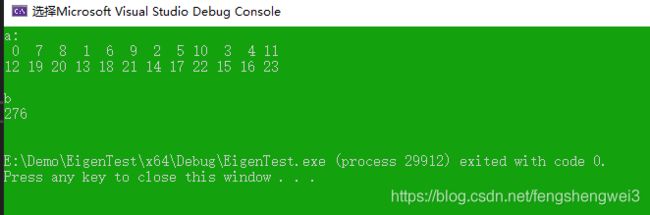
//a有三个维度,我们沿着前两个维度降维,降维的结果是一个一维的Tensor,
Eigen::Tensor b =a.maximum(Eigen::array({ 0, 1 }));
cout << "b" << endl << b << endl << endl;
} 沿着所有维度降维
作为降维的一个特例,可以不传入任何参数,沿着所有的维度进行降维,如下代码所示
void testReduction3()
{
Eigen::Tensor a(2, 3, 4);
a.setValues({ {
{0.0f, 1.0f, 2.0f, 3.0f},
{7.0f, 6.0f, 5.0f, 4.0f},
{8.0f, 9.0f, 10.0f, 11.0f}},
{
{12.0f, 13.0f, 14.0f, 15.0f},
{19.0f, 18.0f, 17.0f, 16.0f},
{20.0f, 21.0f, 22.0f, 23.0f}} });
cout << "a:" << endl << a << endl << endl;
Eigen::Tensor b = a.sum();
cout << "b" << endl << b << endl << endl;
} 下面列出来相关的函数
sum(const Dimensions& new_dims)
sum()
mean(const Dimensions& new_dims)
mean()
maximum(const Dimensions& new_dims)
maximum()
minimum(const Dimensions& new_dims)
minimum()
//prod()
prod(const Dimensions& new_dims)
prod()
all(const Dimensions& new_dims)
all()
any(const Dimensions& new_dims)
any()
reduce(const Dimensions& new_dims, const Reducer& reducer)
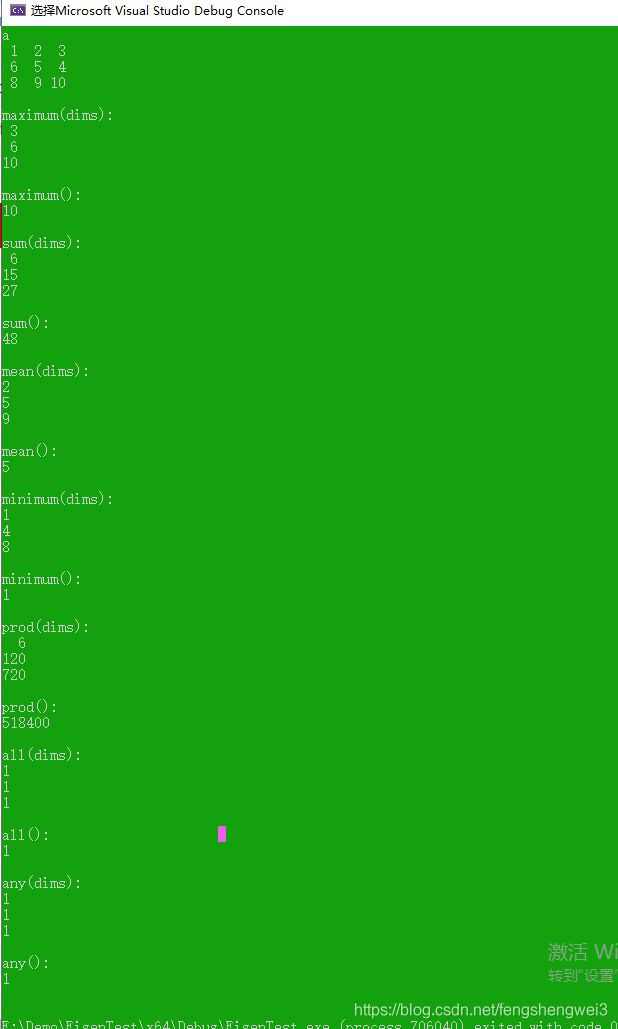
void testReduction4()
{
// Create a tensor of 2 dimensions
Eigen::Tensor a(3, 3);
a.setValues({ {1, 2, 3}, {6, 5, 4},{8, 9, 10} });
//
Eigen::array dims = { 1 }; //沿着第二个维度降维
Eigen::array dims2 = { 0 }; //沿着第一个维度降维
Eigen::Tensor maximum = a.maximum(dims);
cout << "a" << endl << a << endl << endl;
cout << "maximum(dims):" << endl << a.maximum(dims) << endl << endl;
cout << "maximum():" << endl << a.maximum() << endl << endl;
cout << "sum(dims):" << endl << a.sum(dims) << endl << endl;
cout << "sum():" << endl << a.sum() << endl << endl;
cout << "mean(dims):" << endl << a.mean(dims) << endl << endl;
cout << "mean():" << endl << a.mean() << endl << endl;
cout << "minimum(dims):" << endl << a.minimum(dims) << endl << endl;
cout << "minimum():" << endl << a.minimum() << endl << endl;
//返回相应维度元素的乘积
cout << "prod(dims):" << endl << a.prod(dims) << endl << endl;
cout << "prod():" << endl << a.prod() << endl << endl;
//如果相应维度的元素都是大于0 ,则相应维度的降维结果为1 ,否则为0
cout << "all(dims):" << endl << a.all(dims) << endl << endl;
cout << "all():" << endl << a.all() << endl << endl;
//如果相应维度的元素某个大于0 ,则相应维度的降维结果为1 ,否则为0
cout << "any(dims):" << endl << a.any(dims) << endl << endl;
cout << "any():" << endl << a.any() << endl << endl;
}
7.扫描操作
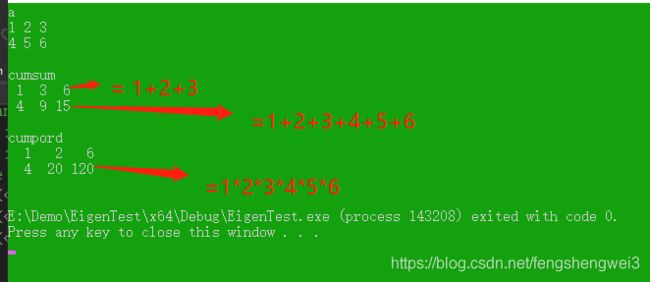
Scan操作返回与原始tensor同维度的tensor,该操作沿着指定的轴执行“包含扫描”,即:它计算降维操作的运行总数(沿着降维轴),如果是求和操作,那么它计算的是沿着降维轴的累加求和
void testScan()
{
// Create a tensor of 2 dimensions
Eigen::Tensor a(2, 3);
a.setValues({ {1, 2, 3}, {4, 5, 6} });
// Scan it along the second dimension (1) using summation
Eigen::Tensor b = a.cumsum(1);
Eigen::Tensor c = a.cumprod(1);
// The result is a tensor with the same size as the input
cout << "a" << endl << a << endl << endl;
cout << "cumsum" << endl << b << endl << endl;
cout << "cumpord" << endl << c << endl << endl;
}
8 .卷积操作
卷积操作跟图像课程里面讲的卷积一样,这里不再详述
void testConvolve()
{
Eigen::Tensor input(3, 3, 7, 11);
Eigen::Tensor kernel(2, 2);
Eigen::Tensor output(3, 2, 6, 11);
input.setRandom();
kernel.setRandom();
Eigen::array dims= { 1, 2 }; // Specify second and third dimension for convolution.
output = input.convolve(kernel, dims);
cout << "Kernel:" << endl << kernel << endl;
cout << "Output:" << endl << output << endl;
//下面手工计算卷积,对比结果
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 2; ++j) {
for (int k = 0; k < 6; ++k) {
for (int l = 0; l < 11; ++l) {
const float result = output(i, j, k, l);
const float expected = input(i, j + 0, k + 0, l) * kernel(0, 0) +
input(i, j + 1, k + 0, l) * kernel(1, 0) +
input(i, j + 0, k + 1, l) * kernel(0, 1) +
input(i, j + 1, k + 1, l) * kernel(1, 1);
cout << result << "," << expected << endl;
}
}
}
}
} 9.几何运算
这些运算得到的张量与原来的张量维数不同。它们可以用来访问张量的片,用不同的维度查看它们,或者用附加数据填充张量
(1) reshape(const Dimensions& new_dims)
返回输入张量的view,该张量已被重新构造为指定的新维。参数new_dims是一个索引值数组。得到的张量的秩等于元素的个数。
void testReshape()
{
Eigen::Tensor a(2, 3);
a.setValues({ {0.0f, 100.0f, 200.0f}, {300.0f, 400.0f, 500.0f} });
//说明: array 的类型需要为Eigen:DenseIndex ,如果是int, 则编译不过
Eigen::array one_dim = { 3 * 2 };
Eigen::Tensor b = a.reshape(one_dim);
array three_dims = { {3, 2, 1} };
Eigen::Tensor c = a.reshape(three_dims);
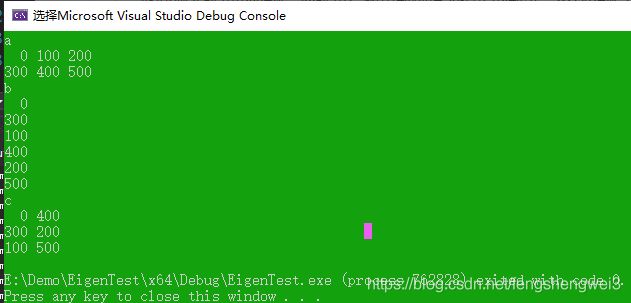
cout << "a" << endl << a << endl;
cout << "b" << endl << b << endl;
cout << "c" << endl << c << endl;
}
(2) shuffle(const Shuffle& shuffle)
返回输入张量的副本,该张量的维数已根据指定的排列重新排序。参数是一个索引值数组。它的大小是输入张量的秩。它必须包含0、1、…,秩- 1(顺序根据需要随便设置)。输出张量的第i维等于输入张量的第i维洗牌的大小。
void testShuffle()
{
Eigen::Tensor input(2, 3, 3);
input.setRandom();
Eigen::array shuffle = { 1, 2, 0 };
Eigen::Tensor output = input.shuffle(shuffle);
cout << "input:" << endl << input << endl;
cout << "output:" << endl << output << endl;
cout << (output.dimension(0) == 3) < (3) stride(const Strides& strides)
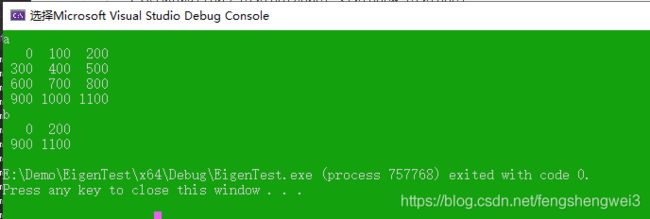
返回一个子张量,从原来张量中按照strides的步长取元素
void testStrides()
{
Eigen::Tensor a(4, 3);
a.setValues({ {0, 100, 200}, {300, 400, 500}, {600, 700, 800}, {900, 1000, 1100} });
Eigen::array strides = { 3, 2 };
Eigen::Tensor b = a.stride(strides);
cout << "a" << endl << a << endl;
cout << "b" << endl << b << endl;
}
(4) slice(const StartIndices& offsets, const Sizes& extents)
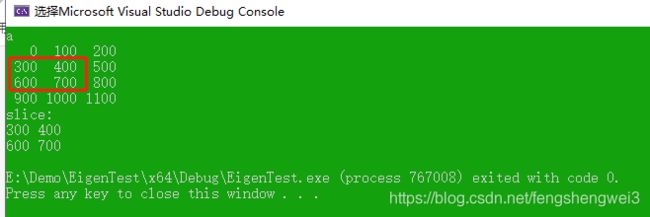
返回给定张量的子张量。对于每个维i,切片是由存储在输入张量的偏移量[i]和偏移量[i] +区段[i]之间的系数构成的
void testSlice()
{
Eigen::Tensor a(4, 3);
a.setValues({ {0, 100, 200}, {300, 400, 500},
{600, 700, 800}, {900, 1000, 1100} });
Eigen::array offsets = { 1, 0 };
Eigen::array extents = { 2, 2 };
Eigen::Tensor slice = a.slice(offsets, extents);
cout << "a" << endl << a << endl;
cout << "slice:" << endl << slice << endl;
} (5) chip(const Index offset, const Index dim)
chip是slice的特殊形式,
void testChip()
{
Eigen::Tensor a(4, 3);
a.setValues({ {0, 100, 200}, {300, 400, 500},
{600, 700, 800}, {900, 1000, 1100} });
Eigen::Tensor row_3 = a.chip(2, 0);
Eigen::Tensor col_2 = a.chip(1, 1);
cout << "a" << endl << a << endl;
cout << "row_3" << endl << row_3 << endl;
cout << "col_2" << endl << col_2 << endl;
}
(6)reverse(const ReverseDimensions& reverse)
返回输入张量的一个视图,该视图在维的一个子集上反转系数的顺序。参数reverse是一个布尔值数组,指示系数的顺序是否应该在每个维上反转(true表示反转,false表示不反转)。这个操作保持了输入张量的维数。
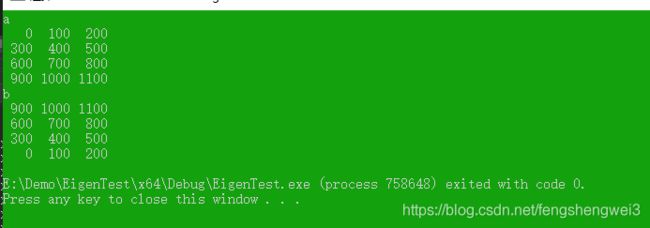
void testReserve()
{
Eigen::Tensor a(4, 3);
a.setValues({ {0, 100, 200}, {300, 400, 500},
{600, 700, 800}, {900, 1000, 1100} });
Eigen::array reverse = { true, false }; //表示第一维反转,第二维不反转
Eigen::Tensor b = a.reverse(reverse);
cout << "a" << endl << a << endl << "b" << endl << b << endl;
}
相关测试代码见:https://github.com/Mayi-Keiji/EigenTest.git
结束~~