导图
前缀和
前缀和常用于快速地求解区间范围内的元素总和。
一维前缀和
设元素存储在a[N]中,我们设计一个数组s[N],s[i]对应第一个元素到第i个元素的总和,即\(s[i]=a[1]+a[2]+...+a[i]\)。
一维前缀和的维护公式为:\(s[i]=s[i-1]+a[i]\)。
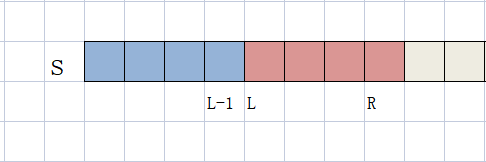
若我们想快速求出区间\([L,R]\)范围内的元素总和。
我们可以利用前缀和快速求解:\(sum_{[L,R]}=s[R]-s[L-1]\)。
可通过图片加深理解。
二维前缀和
设元素存储在a[N][N]中,我们设计一个数组s[N][N],用来存储a[1][1]开始的矩阵总和。
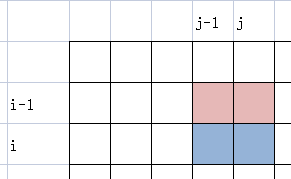
s[i][j]的含义可看下图。a[N][N]为无色部分,s[N][N]为深色部分。
那么如何维护二维的前缀和数组呢?可观察下图:
可发现s[i][j]的面积由橙色区域s[i-1][j]与蓝色区域s[i][j-1]组成后,再去掉重叠部分紫色区域s[i-1][j-1]后加上本身位置的内容a[i][j]得到。
故得到公式:\(s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]\)。
若我们想快速的求出某个子矩阵的元素和,可进行如下处理。
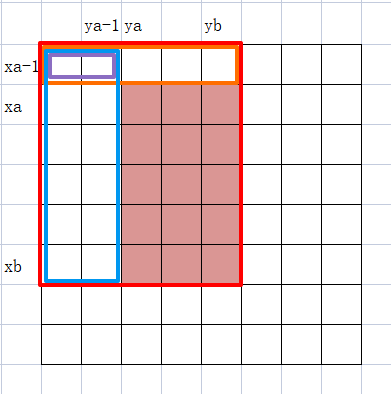
我们设子矩阵左上位置为(xa,ya),右下位置为(xb,yb)。从而确定子矩阵的形状。
观察下图,可以发现,子矩阵的总和可由红色区域s[xb][yb]去掉蓝色区域s[xb][ya-1]和橙色区域s[xa-1][yb]后,再加上重复减的紫色区域s[xa-1][ya-1]后得到。即,公式为:\(sum_{子矩阵}=s[xb][yb]-s[xb][ya-1]-s[xa-1][yb]+s[xa-1][ya-1]\)。
差分
差分常用于对连续的某个区域快速进行增加和减少的值的操作。
一维差分
设元素存储在a[N]中,我们设计一个差分数组b[N],b[i]对应a[i]与a[i-1]的差值,即\(b[i]=a[i]-a[i-1]\)。
若我们对差分数组b进行前缀和处理,可发现存在逆元特性,前缀和的内容等于原数组a的内容。
s[1]=b[1]=a[1]
s[2]=s[1]+b[2]=a[1]+a[2]-a[1]=a[2]
s[3]=s[2]+b[3]=a[2]+a[3]-a[2]=a[3]
...
s[i]=s[i-1]+b[i]=a[i-1]+a[i]-ba[i-1]=a[i]
若我们对b[i]的对加上x。
再进行前缀和处理。
可发现,相当于从i到最后的n,对所有的原数组内容加上了x。
故,若想对\([L,R]\)的范围的值都加上x。可通过三步实现。
b[L]+=xb[R+1]-=x- 前缀和处理查分数组b
二维差分
设元素存储在a[N][N]中,我们设计一个差分数组b[N][N],用来存储a数组中相邻元素的差值。
二维差分维护公式为:\(b[i][j]=a[i][j]-a[i][j-1]-(a[i-1][j]-a[i-1][j-1])=a[i][j]-a[i][j-1]-a[i-1][j]+a[i-1][j-1]\)。
若我们对差分数组b进行前缀和处理,存在逆元特点,前缀和结果为原数组a中的内容。
若我们对差分数组b[xa][yb]+=x,再对差分数组求前缀和。可发现,(xa,ya)到(n,n)的原数组内容都加上了x。
若我们想快速地对某个子矩阵区域的元素和加减值。
我们设子矩阵左上位置为(xa,ya),右下位置为(xb,yb)。从而确定子矩阵的形状。
观察下图
可发现若想对子矩阵区域加上x,可先将红色区域b[xa][ya]加上x,在将橙色区域b[xa][yb+1]与蓝色区域b[xb+1][ya]减去x进行抵消,再将重复减去的紫色区域b[xb+1][yb+1]的内容加上来。
b[xa][ya]+=xb[xa][yb+1]-=xb[xb+1][ya]-=xb[xb+1][yb+1]+=x
之后再对差分数组进行前缀和处理即可。
习题强化
习题代码在项目OIAlgorithm中。
P1115 最大子段和
P1719 最大加权矩形
P2367 语文成绩
P3397 地毯