数理逻辑

数理逻辑
——是研究演绎推理的一门学科，用数学的方法来研究推理的规律统称为数理逻辑。
主要研究内容：
命题逻辑
命题的基本概念
命题联结词
命题公式
命题的范式
命题逻辑推理理论
谓词逻辑
谓词的基本概念
谓词公式
公式的标准型
谓词逻辑推理理论

第一章 命题逻辑

命题逻辑也称命题演算。
研究内容：
命题的基本概念
命题联结词
命题公式
命题的范式
命题逻辑推理理论

1.1 命题及其表示

一、命题
命题：能判断真假的陈述句。
该定义有两层含义：
（1）命题是陈述句。其它的语句，如疑问句、祈使句、感叹句均不是命题；
（2）这个陈述句表示的内容可以分辨真假，而且不是真就是假，不能不真也不假，也不能既真又假。
命题的真值
作为命题的陈述句所表示的判断结果称为命题的真值
真值只取两个值：真或假。凡是与事实相符的陈述句是真命题，而与事实不符合的陈述句是假命题。
通常用1（或字母T）表示真，用0（或字母F）表示假。
注意：
一切没有判断内容的句子都不能作为命题，如命令句、感叹句、疑问句、祈使句、二义性的陈述句等。
结论：命题一定是陈述句，但并非一切陈述句都是命题。
命题的真值有时可明确给出，有时还需要依靠环境、条件、实际情况时间才能确定其真值。
命题的分类：
1.原子命题(简单命题)：不能再分解为更为简单命题的命题。
例如：雪是黑色的
2.复合命题：由联结词、标点符号和原子命题复合而成的命题。
例如：如果今天晚上有星星，那么明天就是晴天。
命题标识符
大写英文字母P，Q，R等表示简单命题
例：
P：今天下雨
命题常元：表示确定命题
命题变元：只表示任意命题的位置标志

1.2 命题联结词

在数理逻辑中，复合命题是由原子命题与逻辑联结词组合而成。
联结词：联结命题的词。联结词又称逻辑联结词或真值联结词。
联结词
一、否定联结词“¬”
设P为一命题，P的否定是一个新命题，记作“¬P”，读作“非P”。
“¬”是一元联结词。

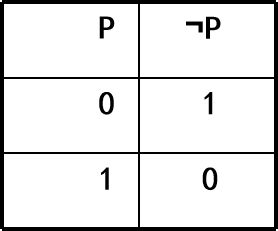
二、合取联结词“∧”
二元联结词。读作“与”、“且”
例如：
（1） P：今天下雨
Q：明天下雨 P∧Q：今天下雨并且明天下雨。
（2）小明与小华是兄弟。
（3）我们去种树与房间里有一台电视机。

三、析取联结词“∨”
读作“或”
例：
灯泡有故障或开关有故障。

注意：
运算∨上一杠：表示“可兼或”，不能表示“排斥或”

例：他乘火车去北京或乘飞机去北京。

注：“排斥或”用∨杠表示；
四、蕴含联结词“右箭头”（条件联结词）
相当于自然语言中的“若…则…”、
“如果…就…”、“只有…才…”，
真值表如右图。

注意和自然语言的区别：
（1）善意的推定；
（2）前件和后件可以
没有任何联系

四、蕴含联结词“”（条件联结词）
举例
（a）P：我拿起一本书 。
Q：我一口气读完了这本书 。
PQ：如果我拿起一本书，则我一口气读完了这本书。
(b) P：月亮出来了
Q：3×3=9
PQ ：如果月亮出来了，则3×3=9。
五、等价词“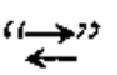
”
读作“当且仅当”

也可以写为


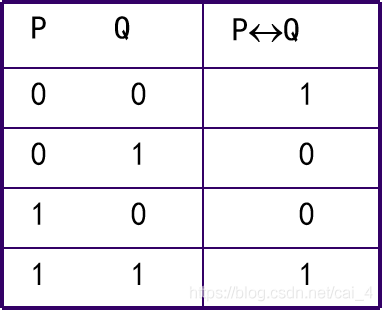
说明：
1）联结词是句子与句子之间的联结
（2）联结词是两个句子真值之间的联结，而非句子的具体含义的联结，两个句子之间可以无任何的内在联系；

约 定：
为了不使句子产生混淆，作如下约定，命题联结词之优先级如下：
1）否定→合取→析取→条件→等价
（2）同级的联结词，按其出现的先后次序(从左到右)
（3）若运算要求与优先次序不一致时，可使用括号；同级符号相邻时，也可使用括号。括号中的运算为最优先级。

1.3 命题公式与翻译

1、命题公式：由命题变元、联结词和圆括号按一定规则组成的合式公式。
合式公式定义如下：
（1）单个命题变元本身是一个合式公式；
（2）如G是公式，则(┐G)也是合式公式；
（3）如G，H是公式，则(G∧H)、(G∨H)、(G→H)、(GH)也是合式公式；
（4）当且仅当能够有限次地使用规则1-3后产生的符号串才是合式公式。
符号串：P∧(Q∨R)→(Q∧(┐S∨R))；
┐P∧Q； P→(┐(P∧Q))；
((P→Q)∧(R→Q))双箭头(P→R)。
等都是命题公式。
2、命题符号化（翻译）
命题逻辑里讨论的对象是命题公式，而日常生活中的推理问题是用自然语言描述的，因此要进行推理演算必须先把自然语言符号化（或形式化）成逻辑语言，即命题公式。然后再根据逻辑演算规律进行推理演算。

1.4. 真值表与等价公式

一、定义：
设P1、P2、…、Pn是出现在公式G中的所有命题变元，指定P1、P2、…、Pn一组真值，则这组真值称为G的一个解释或指派。
一般来说，若有ｎ个命题变元，则应有2^n个不同的指派。将公式G在其所有可能指派下的真值情况列成表，称为G的真值表。
构造真值表的步骤
1)找出给定命题公式中所有的命题变元，列出所有可能的真值。
2)按照优先级从高到低写出命题公式的各层次。
3)对应每个真值，计算命题公式各层次的值，直到最后计算出整个命题公式的值。
三个公式的真值表如下：

永真公式 永假公式 可满足公式
二、公式的分类
1）永真公式(重言式)
（2）永假公式(矛盾式）
（3）可满足式
三、等价公式：

三、等价公式：
1.定义
设G、H是公式，如果在任意分量指派下，G与H的真值相同，则称公式G、H是等价的，记作G双向箭头H。

2.基本等价公式

证明两个公式等价的方法
真值表
等价公式推导


例．A、B、C、D四人比赛，观众甲、乙、丙预报比赛名次为：
甲：C第一，B第二 乙：C第二，D第三 丙：A第二，D第四
比赛结束发现甲乙丙每人各说对一半，试问实际名次（无并列者）。


某件事是甲、乙、丙、丁四人中某一人干的，询问四人后回答如下：
1）甲说是丙干的；
2）乙说我没干
3）丙说甲说的不符合事实
4）丁说是甲干的
若其中三人说的对，一人说的不对，问谁干的？

1.5重言式与蕴含式

一、重言式
1.定义：
重言式就是永真公式
定理1：任何两个重言式的合取或析取，仍然是一个重言式。
定理2：一个重言式，对同一分量用任何公式置换，其结果仍为重言式。
定理3：设A，B为两个命题公式，A →B当且仅当A→B为一重言式。
2.证明公式为重言式的方法：
真值表法
等价公式推导
二、蕴含式：1.定义：
当且仅当P→Q是一个永真式，则称“P蕴含Q”，记为P⇒Q

对P→Q来说：Q→P称作它的逆换式,非P→非Q 称作它的反换式，非Q→非P称作它的逆反式，有如下关系；
P→Q 双箭头Q →非P
Q→P 等价P→非Q




4.蕴含式的常用性质

1.6 其它联结词

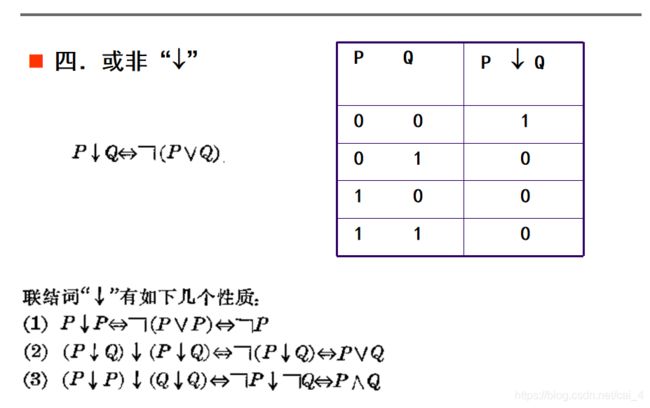
两个命题变元共能构成16种不等价的命题，而这些情况用9个联结词能够全部表示出来，所以 9个联结词就足够了

最小联结词组：必须是功能完备的，即任何命题公式都可以由最小联结词组中所包含的联结词来表示。对于最小联结词组，删除其中任何一个联结词就不能把所有的命题表达出来。

1.7 对偶与范式

二、范式


注意：
3.范式的求解方法
定理1. 对于任意命题公式，都存在与其等价的析取范式和合取范式。

2）重复使用德摩根定律将否定号移到各个命题变元的前端，并消去多余的否定号；
3）重复利用分配律，可将公式化成一些合取式的析取，或化成一些析取式的合取；

5. 主析取范式
1）极小项
定义 ：在含有n个命题变元P1、P2、P3、…、Pn的合取式中，若每个命题变元与其否定不同时存在，但二者之一恰好出现一次且仅一次，则称此合取式为关于P1、P2、P3、…、Pn的一个极小项；
对于n个命题变元，可构成2^n个极小项

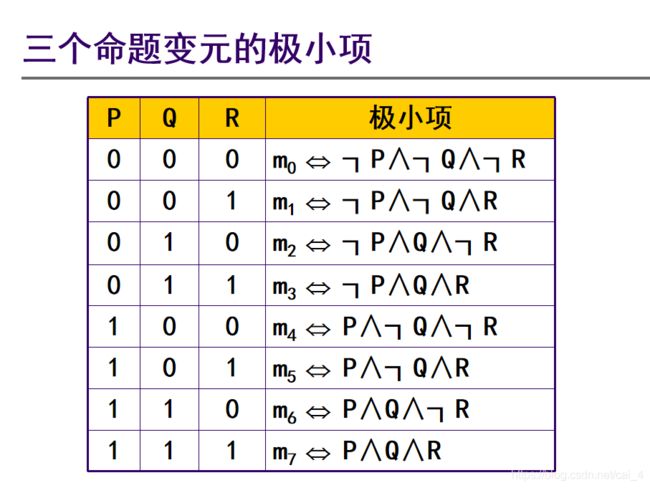
极小项的性质：
没有两个小项等价 ；
◆每个小项当其真值指派与对应的编码相同时，真值为1，其它情况均为0 ；
◆任意两个不同小项的合取为永假式；
◆所有极小项的析取为永真公式；
2）主析取范式
定义：
给定的析取范式中，每一个合取式都是极小项，则称该范式为主析取范式
求主析取范式的方法：
a)真值表法
公式对应的真值表中真值结果为真的所有的行，找到其每一个分量指派所对应的极小项，将这些极小项进行析取即可得到相应的主析取范式。
b)等价公式推导法
◆先求出该公式所对应的析取范式；
◆去掉重复出现的命题变元、析取范式中的永假式；
◆若析取范式的某一个合取式缺少该命题公式中所规定的命题变元，则可用公式：(Ｐ∨非Ｐ)∧Q 等价Q将命题变元P补进去，并利用分配律展开；
◆将相同的极小项合并，同时利用交换律进行顺序调整，由此可转换成标准的主析取范式；
◆还可以进一步用抽象表示法表示；
6. 主合取范式
1）极大项
定义 ： 在含有n个命题变元P1、P2、P3、…、Pn的析取式中，若每个命题变元与其否定不同时存在，但二者之一恰好出现一次且仅一次，则称此析取式为关于P1、P2、P3、…、Pn的一个极大项
对于n个命题变元，可构成2^n个极大项

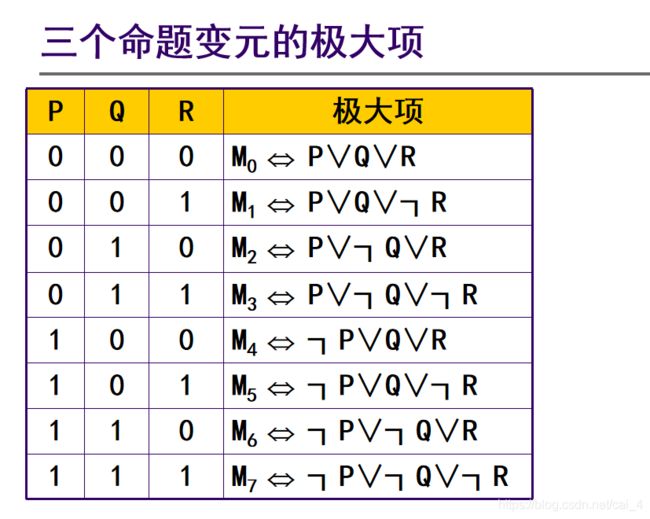
极大项的性质：没有两个极大项等价 ；
◆每个极大项当其真值指派与对应的编码相同时，真值为0，其它情况均为1 ；
◆任意两个不同极大项的析取为永真式；
◆所有极大项的合取为永假公式；
2）主合取范式
定义：
给定的合取范式中，每一个析取式都是极大项，则称该范式为主合取范式
求主合取范式的方法：
a)真值表法
公式对应的真值表中真值结果为假的所有的行，找到其每一个解释所对应的极大项，将这些极大项进行合取即可得到相应的主合取范式。
b)等价公式推导法
◆先求出该公式所对应的合取范式；
◆去掉重复出现的命题变元、合取范式中的永真式；
◆若合取范式的某一个析取式缺少该命题公式中所规定的命题变元，则可用公式：(Ｐ∧ 非Ｐ) ∨Q 等价Q将命题变元P补进去，并利用分配律展开；
◆相同的极大项合并，同时利用交换律进行顺序调整，由此可转换成标准的主合取范式；
◆还可以进一步用抽象表示法表示；
7 主析取范式和主合取范式之间的转换

8、 范式的应用
判断公式类型
判断公式是否等价
判断公式为真或为假的分量指派

1.8 推理理论

二、判断有效结论的常用方法
真值表法
直接证法
间接证法
利用定义
1.真值表法：
设P1，P2，……，Pn是出现于前提H1，H2，……，Hm和结论C中的全部命题变元，假定对P1，P2，……，Pn作了全部的真值指派，这样就能对应地确定H1，H2，……，Hm和C的所有真值.

对于真值表法，仅适用于命题变元少的情况。

在数理逻辑中，主要的推理规则有：
① P规则（前提引入规则）：前提在推导的过程中任何时候都可以使用；
②Ｔ规则（结论引用规则）：在推导过程中，前面得出的结论可以在之后的任何地方使用；
3.间接证法
(1)反证法(归谬法）
(2)CP规则