关于位姿变换的一点体会
关于位姿变换的一点体会
- 1.题外话
- 2.刚体的位姿变换
-
- 2.1 位姿变换的定义
- 2.2 旋转矩阵的具体形式
-
- 2.2.1 二维情况
- 2.2.2 三维情况
- 3.旋转方向
- 4.平移方向
1.题外话
对于刚体的位姿变换问题,以前总觉得很简单,不就是个旋转平移嘛。可是几天手动做了的坐标变换却做了很久才做好。究其原因,还是有些问题没弄清楚。所以,今天在此写篇博客,彻底把这个过程捋一捋。
2.刚体的位姿变换
2.1 位姿变换的定义
确实,刚体的姿态变换就两部分:旋转和平移。先来看看书上是怎么介绍旋转和平移的。在《视觉slam十四讲》中,对于这部分内容是这样将的:
我们设某个单位正交基 ( e 1 , e 2 , e 3 ) (e_{1},e_{2},e_{3}) (e1,e2,e3)经过一次旋转,变成了 ( e 1 ′ , e 2 ′ , e 3 ′ ) (e'_{1},e'_{2},e'_{3}) (e1′,e2′,e3′)。那么,对于同一个向量 a a a(注意该向量并没有随着坐标系的旋转而发生运动),它在两个坐标系下的坐标为 [ a 1 ; a 2 ; a 3 ] T [a_{1}; a_{2}; a_{3}]^T [a1;a2;a3]T 和 [ a ′ 1 ; a ′ 2 ; a ′ 3 ] T [a′_{ 1}; a′_{ 2}; a′ _{3}]^T [a′1;a′2;a′3]T。根据坐标的定义,有:

为了描述两个坐标之间的关系,我们对上面等式左右同时左乘 [ e 1 T , e 2 T , e 3 T ] T [e^T_{1},e^T_{2},e^T_{3}]^T [e1T,e2T,e3T]T,那么左边的系数变成了单位矩阵,所以

我们把中间的阵拿出来,定义成一个矩阵 R R R。这个矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的,那么这个矩阵也是一样的。可以说,矩阵 R R R 描述了旋转本身。因此它又称为旋转矩阵。
在欧氏变换中,除了旋转之外还有一个平移。考虑世界坐标系中的向量 a a a,经过一次旋转(用 R R R 描述)和一次平移 t t t 后,得到了 a ′ a′ a′,那么把旋转和平移合到一起,有:
a ′ = R a + t a′= Ra + t a′=Ra+t
其中, t t t 称为平移向量。相比于旋转,平移部分只需把这个平移量加到旋转之后的坐标上,显得非常简洁。
以上内容摘自《视觉slam十四讲》第三章中的内容。
2.2 旋转矩阵的具体形式
从上面的内容可以看到,旋转矩阵是由两组基向量的内积组成。接下来再看看沿各个坐标轴进行旋转的旋转矩阵怎样写。
2.2.1 二维情况
对于二维的情况,比较简单。旋转矩阵(旋转方向为逆时针)为:
R = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] R= \left[ \begin{matrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{matrix} \right] R=[cos(θ)sin(θ)−sin(θ)cos(θ)]
2.2.2 三维情况
绕x轴进行旋转(在yz平面逆时针旋转)
R = [ 1 0 0 0 c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) ] R= \left[ \begin{matrix} 1& 0& 0\\ 0&cos(\theta) & -sin(\theta)\\ 0&sin(\theta) & cos(\theta) \end{matrix} \right] R=⎣⎡1000cos(θ)sin(θ)0−sin(θ)cos(θ)⎦⎤
绕y轴进行旋转(在xz平面逆时针旋转)
R = [ c o s ( θ ) 0 − s i n ( θ ) 0 1 0 s i n ( θ ) 0 c o s ( θ ) ] R= \left[ \begin{matrix} cos(\theta) & 0& -sin(\theta)\\ 0&1&0 \\ sin(\theta)& 0& cos(\theta) \end{matrix} \right] R=⎣⎡cos(θ)0sin(θ)010−sin(θ)0cos(θ)⎦⎤
绕z轴进行旋转(在xy平面逆时针旋转)
R = [ c o s ( θ ) − s i n ( θ ) 0 s i n ( θ ) c o s ( θ ) 0 0 0 1 ] R= \left[ \begin{matrix} cos(\theta) & -sin(\theta)& 0\\ sin(\theta)& cos(\theta)& 0\\ 0&0&1 \\ \end{matrix} \right] R=⎣⎡cos(θ)sin(θ)0−sin(θ)cos(θ)0001⎦⎤
3.旋转方向
下面来考虑一个简单的问题。
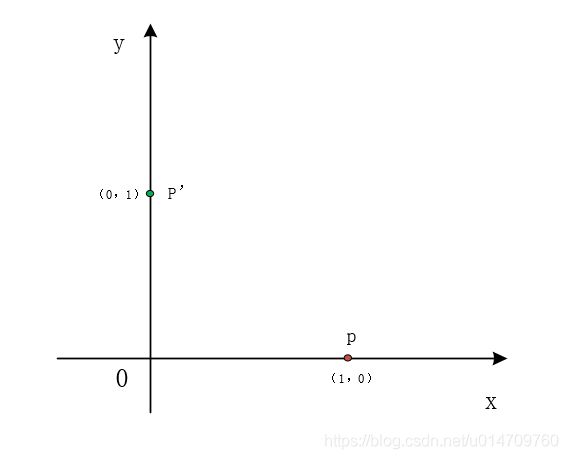
问题:将点 p = ( 1 , 0 ) p =(1,0) p=(1,0),按照旋转矩阵 R R R进行旋转,旋转后的坐标为多少?
R = [ c o s ( θ ) − s i n ( θ ) s i n ( θ ) c o s ( θ ) ] , θ = π / 2 R = \left[ \begin{matrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{matrix} \right] ,\theta=\pi/2 R=[cos(θ)sin(θ)−sin(θ)cos(θ)],θ=π/2
这个问题很简单,口算都可以算出答案是 p ′ = ( 0 , 1 ) p'=(0,1) p′=(0,1)。
但这里面有些问题需要搞清楚。按照旋转矩阵 R R R进行旋转,我们将点 p = ( 0 , 1 ) p =(0,1) p=(0,1)变换为了 p ′ = ( 1 , 0 ) p'=(1,0) p′=(1,0)。相当于把点 p p p逆时针旋转了 π / 2 \pi/2 π/2。这并没有什么问题。在上一节的旋转矩阵的定义中,我们也说了这种形式的旋转矩阵是进行逆时针旋转。
但是问题在于,很多情况下点的位置是固定的,它并不会发生变化。旋转之后发生变化的是坐标系。也就是说,旋转过后,点 p p p的实际位置并没有变,它还是在那个位置。但是它的坐标变了( p ′ = ( 0 , 1 ) p'=(0,1) p′=(0,1)),也就是所在的坐标系变了。那坐标系是怎么旋转的呢?刚好与坐标旋转的方向相反——顺时针旋转。

这个道理同时适用于三维的情况。
我觉得,能把这个问题想清楚很重要。
4.平移方向
进行平移变换的时候,同样存在上面的问题。
我们可以考虑一下。将点 p = ( 1 , 1 ) p = (1,1) p=(1,1)按向量 ( 1 , 2 ) (1,2) (1,2)进行平移,很显然平移后的坐标为 p ′ = ( 2 , 3 ) p'=(2,3) p′=(2,3)。如下图所示:
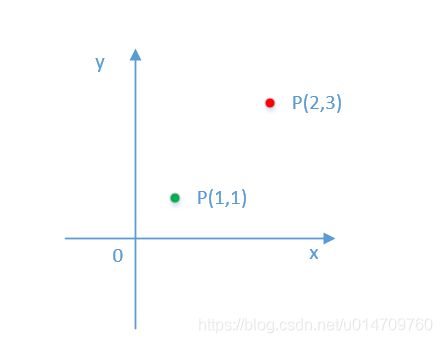
同样,很多情况下点的位置是固定的,变化的是坐标。所以,如果点的位置不变,在进行平移之后点的坐标变为了 p ′ = ( 2 , 3 ) p'=(2,3) p′=(2,3),那只能是坐标系进行了平移。那坐标系是怎么平移的呢?——与坐标平移方向相反,按向量 ( − 1 , − 2 ) (-1,-2) (−1,−2)进行平移。如下图所示

总结一下:关于旋转和平移,必须要想清楚是对点(或向量)进行旋转平移还是对坐标系进行旋转平移。