组合导航（七）：卡尔曼滤波

Kalman滤波

导航系统的精度受到 惯性传感器初始化以及算法的误差影响。低成本MEMS传感器由于严重的随机误差，INS输出可能迅速漂移。因此低精度的IMU基本上不能作为导航独立传感器进行使用。
在之前的章节中曾叙述过，对于水平面的速度与姿态角而言，若没有对速度进行持续的优化以消除速度误差，在长时间运动情况下会导致Vn和Ve值产生巨大的误差。同时，姿态角的误差，也需要依靠这些速度值来调节 ——【舒勒效应】。因此，建立精确的速度分量模型是十分重要的（可消除pitch、roll角的误差）。

几类典型的测量更新方式：
1）位置 或坐标更新——“CUPT”
2）速度 或零速度更新——“ZUPT”
3）姿态更新

通过外部测量进行INS更新的方法有很多种：包括卡尔曼滤波(KF)、粒子滤波(PF)和人工智能(AI)。
通常，将惯性导航系统与GPS辅助系统相结合，利用卡尔曼滤波对惯性传感器误差进行估计和补偿。总的来说，卡尔曼滤波器是一种从被噪声污染的测量值中最优估计系统状态误差的算法。这是一个顺序递归算法，提供了一个最佳的误差最小均方差估计。
卡尔曼滤波的优秀之处在于，它使用了所有可用的测量数据，不论它们的精度高低，都可以通过对测量值增加合适的权重来估计当前系统状态。

在惯性导航应用中，卡尔曼滤波用于互补配置，将具有不同噪声特性的同一信号的冗余测量值结合起来，最小化误差。惯导系统能提供良好的高频信息，但由于积分运算，惯导系统的误差随时间不断增大，使得加速度计和陀螺仪的偏置误差在输出端积累。惯性传感器的偏置误差通常出现在传感器输出的低频部分，称为长期误差。另一方面，许多其他导航系统(如GPS)具有良好的低频特性，但容易产生高频噪声。因此，利用KF可以从外部源的准确低频数据中获益，从而限制INS的长期误差。有许多外源可以为INS提供可靠的帮助，包括雷达、GPS、车轮传感器、激光测距和存储的图像数据库。
在下文中将主要考虑全球定位系统作为外部源（由于GPS的准确性，全球可用性和低成本）。

1 离散卡尔曼滤波

卡尔曼滤波要求系统为线性的系统，离散时间的线性系统可描述为：

其中：Wk-1为过程噪声。由于噪声对动态系统的影响表现在状态矢量的多个分量上，因此需要使用一个噪声分布矩阵G来表述噪声与各个状态分量之间的耦合性。

系统的离散时间线性测量方程为：

卡尔曼滤波基于以下假设：

1.状态方程和测量方程均可用线性模型表示；
2.系统噪声Wk以及测量噪声 为不相关的零均值高斯白噪声：


其中，Qk和Rk是正定矩阵。在INS/GPS积分中，
Qk表示与INS误差相关的系统噪声的协方差矩阵，
Rk表示与GPS位置和速度更新相关的测量噪声协方差矩阵。

3.系统初始状态向量xo是一个与过程和测量噪声都不相关的随机向量，因此：

4.初始状态x0以及其协方差矩阵P0是已知的：

2 卡尔曼滤波的流程

KF是一种递归算法，通过状态反馈来估计系统的状态。
如图所示，卡尔曼滤波分为两个环节:(1)预测 /状态更新; (2)校正 /测量更新。
在预测阶段，将系统状态及其协方差从k -1时刻传播到k时刻；然后在校正阶段，使用测量值更新先前的估计，最终得到校正后的状态估计。

2.1 预测与时间更新

根据 k-1 时刻的信息估计 k 时刻的系统状态，称之为“先验估计”——Xk(-)，假定系统噪声为零均值，则 k 时刻的状态估计可写为：

其中Xk-1(+)为上一时刻的最优估计。
同时，卡尔曼滤波还将 上一时刻 k-1 的不确定度传递到下一时刻 k，不确定度通过误差协方差来表示 Pk(-)，也称为先验协方差矩阵：

其中 Pk-1(+)为上一时刻的协方差矩阵的最优估计，由 Pk(-) 和过程噪声Qk得到。

2.2 测量更新与校正

在预测了状态的先验估计之后，当获得外部源的测量信息时，先验估计会得到更正。
测量协方差为Rk，表示测量数据的不确定度。
在测量更新环节中，最重要的一步为：计算卡尔曼增益的加权因子 K

卡尔曼增益使KF在最优估计算法中脱颖而出。
由方程可知，K既依赖于先验协方差Pk(-)，又依赖于测量噪声协方差Rk。如果测量噪声较大(Rk较大)，或者过程噪声较小(Pk(-)较小）时，那么K就会变得相对较小。反之，若过程噪声较大(Pk(-)加大)或测量值的噪声较小时(Rk 较小)，则K相对较大。
当K较大时，测量值将被赋予更多的权重，当K较小时，预测值的权重就相对较大。

当 tk 时刻得到一个新的测量值 Zk 时，将其与基于先验状态估计的预测测量值 HkXk(-) 进行比较。用K对二者误差进行加权，并更新状态向量的预测以生成最佳估计。因此，tk 时刻的状态估计值为：

在更新完系统状态之后，还需对新估计值 Xk(+) 的不确定度进行更新：

对于上式的协方差矩阵更新公式P. D. Joseph 认为，即便求得的卡尔曼增益K 具有细小误差，但传递到上式时依旧会产生能严重的问题。因此，他主张使用一种被称为约瑟夫式的方程的扩展形式：

上式得到的后验协方差在数值上是稳定的，即使K的计算有误差也能得到正确的答案。此外，这种形式的后验误差协方差可以保证Pk(+)是半正定的，有助于避免发散。

在大多数INS应用中，KF更新过程的频率低于预测。例如，通过卡尔曼滤波将GPS和INS集成的典型应用中，预测可能以100hz的频率进行，而更新以1hz的频率进行。下图显示了典型组合系统的预测和更的过程：

离散KF算法的数据流图：

时间更新与测量更新的方程归结如下：

3 卡尔曼滤波 算法步骤

KF由5个步骤组成，算法流程如图所示：

具体步骤如下：

1. 首先，初始化滤波器。这需要为过滤器提供其状态初始估计X0和初始估计中的不确定性P0。Po的估计是基于对初始状态估计的近似精度，通常设置为相对较高的值。同时还需要向滤波器提供系统噪声协方差矩阵Q和测量噪声协方差矩阵R的初始估计值。这些估计值是根据之前的系统经验估算出来的。
2. 预测步骤的第一部分：计算状态转移矩阵，将初始状态从 k-1时刻传递到k时刻, 并表示为Xk(-).
3. 预测步骤的第二部分：计算先验状态的协方差Pk。通过状态转移矩阵、上一时刻的协方差Pk-1、过程噪声协方差Qk-1，以及噪声分布矩阵Gk-1得到。需要注意的是，如果过程噪声较大，Pk就会增大，从而导致先验状态的置信度降低。
4. 测量更新阶段的第一步：计算卡尔曼增益Kk。卡尔曼增益的值取决于先验误差协方差Pk(-)、过程噪声协方差Rk、观测方程中的Hk。Pk(-)越大，增益越大，Rk越大，增益越小。
5. 测量更新阶段的第二步： 继完成预测的第二部分后，当接收到测量值时，先验状态k(-)就会被更新。这一步基于预测的测量值HkXk(-)与实际测量值的差值。根据这一差值进行状态估计的修正，当K较大时，这个差值的权重更大，并添加到先验估计值中，并更新为后验估计值Xk(+)。但当K较小时，从测量中获得的校正信息的权重较小，此时认为先验估计相对准确。
6. 测量更新阶段的第三步：在修正状态估计之后，KF进一步将先验误差协方差Pk(-)更新为后验误差协方差Pk(+)，以表示后验估计的不确定度。
7. 卡尔曼滤波进入下一时刻的状态估计与测量更新。

4 非线性卡尔曼滤波

线性系统是理想化的结果，严格地说，几乎所有的系统都是非线性的（甚至欧姆定律也只是在有限范围内的一个近似，它的线性在超过一定的电压阈值之后就会失效(Simon 2006)）。
由于许多系统非常接近线性，通过对非线性系统进行线性化，可以将线性估计理论应用于非线性系统。在非线性的卡尔曼滤波中，通常将误差状态作为估计值，而不是以系统状态作为状态估计。在GPS/INS的组合导航中，误差状态是由INS状态和辅助源状态(GPS)之间的差值形成的。可用的方法有线性KF (LKF)和扩展卡尔曼滤波（EKF）。

4.1 线性化kalman滤波

对于某一个系统，在标准轨迹附近进行线性化的的方法，被称为线性化卡尔曼滤波（LKF）。此处的标准轨迹通常是已知的，例如，船或客机的航线是预先规划的。对于INS/GPS组合导航系统来说，惯导的输出通常被认为是标准轨迹。
线性化卡尔曼滤波是一个开环结构，其滤波器估计的误差虽然对INS的输出进行校正，但是对INS系统却不构成反馈。

4.2 扩展kalman滤波

轨迹的真值是无法事先知道的，因此通常将轨迹最优估计的结果作为标准轨迹。
当卡尔曼滤波使用先前最优估计的线性化轨迹，而非预定义的标准轨迹时，这种卡尔曼滤波被称为扩展卡尔曼滤波EKF。
EKF对应于闭环的结构，其滤波器估计的误差将反馈到INS系统以矫正其输出：

5 卡尔曼滤波发散控制

对实际系统进行数学表示和线性化的简化过程会导致系统模型的不完善，从而导致KF的发散。这个问题在KF理论的一开始就被发现了，提出的散度控制技术包括在KF过程模型中加入虚拟噪声、Schmidt epsilon技术、有限记忆滤波和渐消记忆滤波。

5.1 KF过程模型中添加虚拟噪声

为了使一个真实系统的数学模型易于处理，必须进行许多简化和假设。此外,大多数系统是非线性的，在使用KF之前必须经过线性化，而这种线性化的方法相当于对系统模型又做了进一步的近似。
这一系列不确定因素，可能会造成KF性能下降，甚至发散。
针对这种情况，可以通过增加过程噪声协方差Q 或者 测量噪声协方差R的方式引入人工噪声。
因此，在实际应用中，Q和R的参数设定一般是基于之前经验所得，并通过调整，以优化系统的性能。

5.2 Schmidt Epsilon方法

在KF中控制离散度的一种方法是为估计误差的协方差矩阵定义一个阈值，使它不低于某个值。在卡尔曼滤波运行过程中，协方差矩阵Pk(-)不断变小，卡尔曼增益K也不断减小，从公式中可以明显看出，当Pk(-)很小时，K趋近0，新的测量值将无法得到足够的权重，滤波器的输出将主要取决于预测值。这一现象被称为Kalman filter incest 。
在协方差阈值化中，通过给计算得到的误差协方差矩阵Pk(-)加上一个符号为正的小量 ，就可以确保卡尔曼增益存在一个下界。这个小量值是根据经验确定：

5.3 有限记忆滤波

在kalman滤波中，最新的估计值Xk(+)是基于从起始时刻到 k 时刻的所有测量值。为了得到最优估计值，滤波器必须考虑到之前的所有测量值。
但是，旧的数据有时不仅无法提供有效信息，反而会导致滤波器出现问题。
因此，在渐消记忆滤波方法中仅使用最近的测量数据，旧的信息将被丢弃。
例如，仅使用测量的最后100个样本进行滤波。

5.4 渐消记忆滤波

有时，一些系统模型只在有限时间内是有效的，在超过一定时限之后，系统模型会发生变化。
针对这种情况，可以通过逐渐减小测量噪声的协方差R的方式，来丢弃旧的测量值，以限制其对最新估计值的影响。
这一思想可以通过引入渐消因子来表示：

其中a是一个正的常数。
随着时间的推移，k变得更大，Rk逐渐减小，因此最近数据所占的权重更大。

同样，将渐消因子a引入误差协方差的计算公式中，也可以起到同样的效果：

其中a的选值>1。

6 卡尔曼滤波例子

6.1 简单导航系统

考虑一个匀加速直线运动的物体。
速度误差随时间的变化率等价于加速度误差，同样，位置误差随时间的变化率等于速度误差，这可以用以下式子表述：

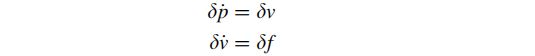
此外，加速度计误差模型采用一阶高斯马尔科夫过程：

那么系统方程用矩阵的形式表示为：

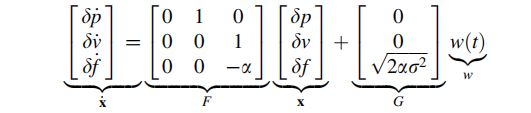
假设GPS的位置更新是连续可用的。通过比较辅助源(GPS)和惯导源(INS)的输出，得到了测量更新方程。因此，提供给卡尔曼滤波器的观测值z为：
其中，误差np为GPS的测量噪声。
将测量z用误差状态矢量x来表示：

若将位置测量更新替换成速度测量更新，则：
其中，误差nv为GPS的测量噪声。
此时，z与误差状态矢量x的关系表示为：

若对位置与速度同步更新，则：

6.2 零速度更新

对于无法获得连续更新的测量值的系统 或者在测量临时拒止的条件下，速度误差以及受到速度误差直接影响的姿态分量与位置分量都有可能不断增大。
与单系统相比，使用ZUPT系统在惯性测量精度上有了显著的提高：
ZUPT的具体步骤如下：

1. 每2-4分钟停车30-60秒。
2. 在停止时获得30—40个速度测量值。
3. 将这些测量用于KF更新或速度曲线拟合。
   ZUPT的优点是不需要额外的设备，操作简单，成本低廉，预测和测量之间不存在同步问题。
   ZUPT的主要限制在于车辆必须立即停止，但这在实际运用中是无法实现的。

6.2.1 通过ZUPT提高测量精度

采用KF等最优估计方法来恢复ZUPT站间INS速度误差的行为。在这样的一个站点，INS输出速度与ZUPT沿三个相互正交的方向的速度之差被反馈给卡尔曼滤波器(如上图)。系统方程与更新测量的类型无关：

其中x是15维的误差状态矢量：

测量更新方程中的H矩阵取决测量值的可信度：

其中：

因此测量更新方程可写为：

其中，Ve0,Vn0,Vu0为零速度更新
下图例举了ZUPT各时间段内的速度与位置的变化趋势。可以明显地看出ZUPT可以防止位置误差不断增长。而在不使用ZUPT的情况下，位置误差会迅速累加，使得位置估计变得不可靠。

ZUPT的性能受两个因素的影响：
1.相邻两个ZUPT之间的持续时间。在这段时间里，速度误差随时间增长。因此ZUPT的间隔时间的选择直接关系到导航精度与性能。
2.ZUPT时间间隔的选择，要使得KF算法收敛并校正INS误差。

ZUPT的重要性包括以下几点：

1. 限制了速度误差的增长，甚至可以将其重置为零。
2. 有助于估计加速度计的偏置误差。
3. 有助于估计三个姿态角的偏差。
   总的来说，ZUPT过程在限制测量误差长期增长方面是有效的。

6.3 坐标更新

在某些导航应用中，可以提供连续的坐标更新，或者是由坐标已精确预定义的CUPT站点提供。
使用CUPT的过程中，物体运动将被临时中断，使得INS的输出可以与辅助源提供的测量坐标进行比较。
在某些应用程序中，坐标更新可以连续提供，也可以在坐标已精确预定义的CUPT站点提供。如果导航系统作为一个独立的INS而不进行更新，我们预计长期的误差会显著增加，即使在使用高度精确的导航级惯性传感器的情况下也是如此。CUPT。物体的运动被中断，以允许INS的输出与辅助源提供的坐标测量进行比较

6.3.1 通过CUPT提高测量精度

CUPT整个过程类似于ZUPT，只是更新的是位置坐标而不是速度。其主要目的在于校正INS的位置误差：在每一CUPT时刻，INS输出的位置与CUPT间的差异将作为卡尔曼滤波器的输入，如下图所示：

与ZUPT系统类似，CUPT系统方程与测量方程可以通过以下给出：