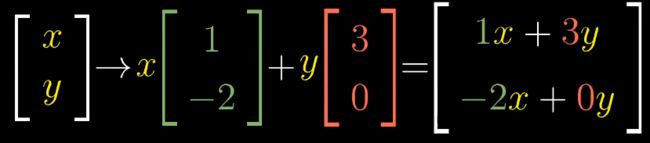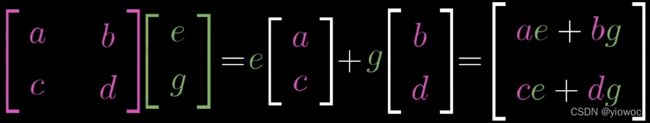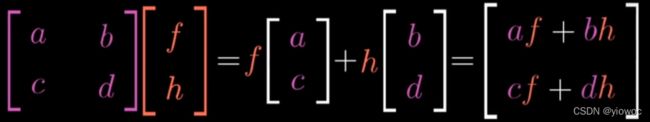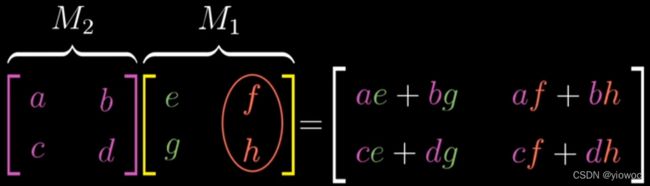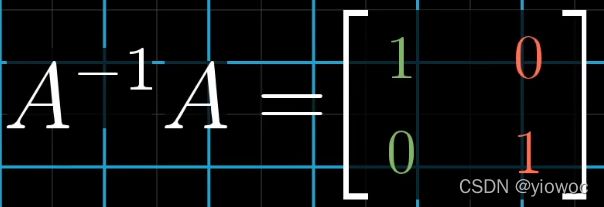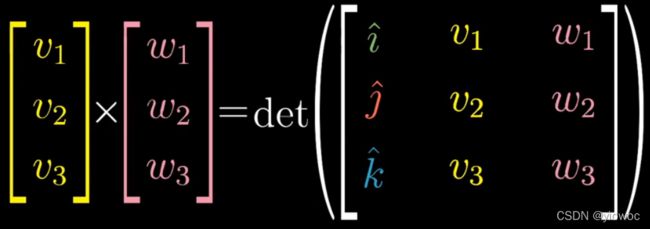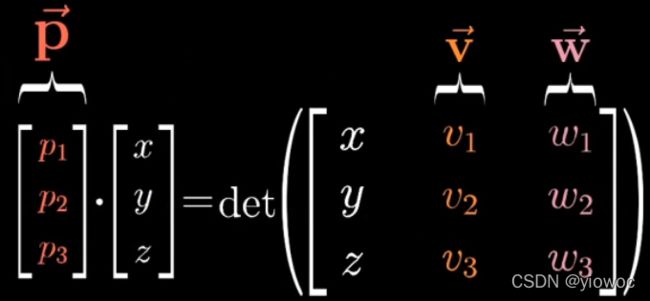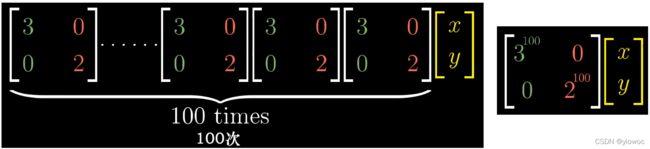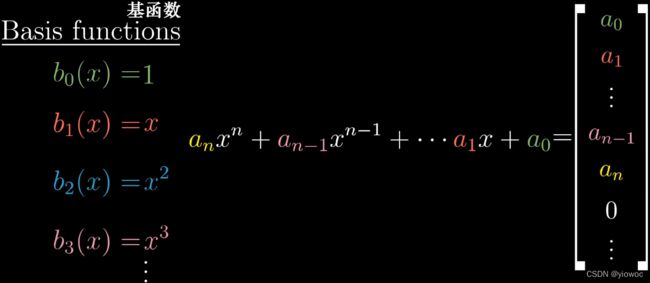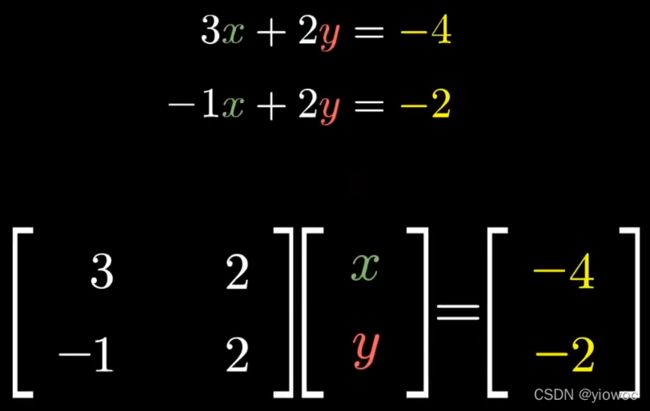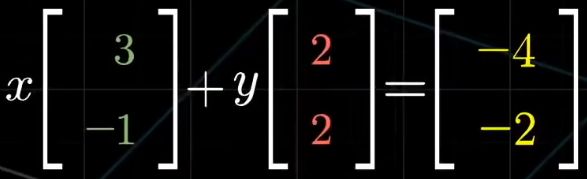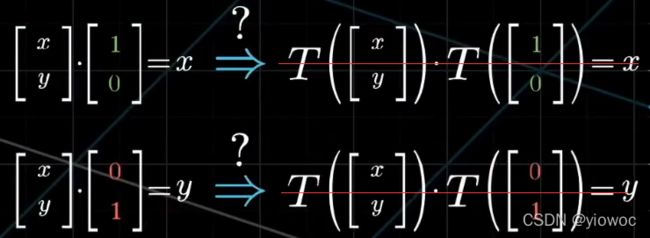线性代数的本质——学习笔记

线性代数的本质——学习笔记

该课程为b站上，3Blue1Brown大佬出的一系列线代视频。花了几天时间好好消化了一下，受益匪浅。欢迎各位没看懂视频的老哥过来看看我的理解，有什么错误也希望能指出，非常感谢。

1-向量究竟是什么

向量的表示

建议：将向量的第一印象看作是在原点上的有向线段

我们可以用中括号框住的竖列的多元数组来表示向量，用以区分向量与坐标点
$$v=\left[\begin{array}{r}v1\\ v2\\ ...\\ v3\end{array}\right]$$

$$a=(x1,x2,...,xn)$$

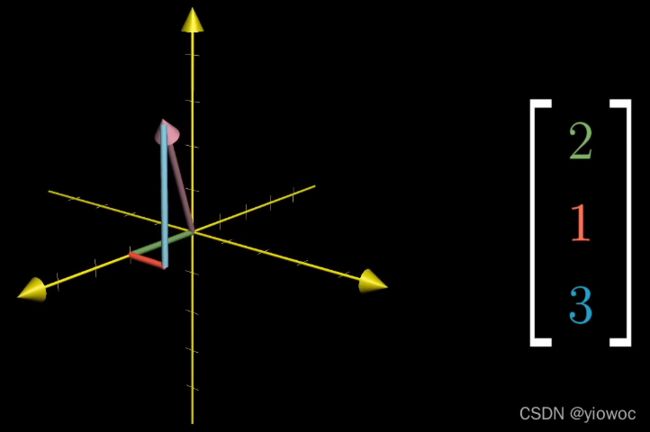
从直观上，想象向量是从由n个轴组成的坐标的原点开始，向量中的每一个数表示该点向对应轴进行延伸的长度

向量加法

将向量视作一种特定的运动，向量加法的效果等于从原点依次进行单个向量的运动效果之和

向量数乘

向量长度成倍数的变化【延伸、缩短、反向】

2-线性组合、张成的空间与基

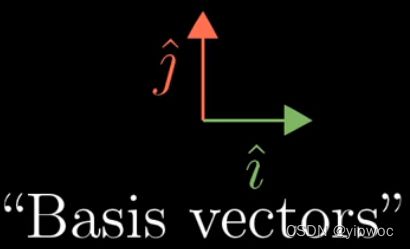
基向量

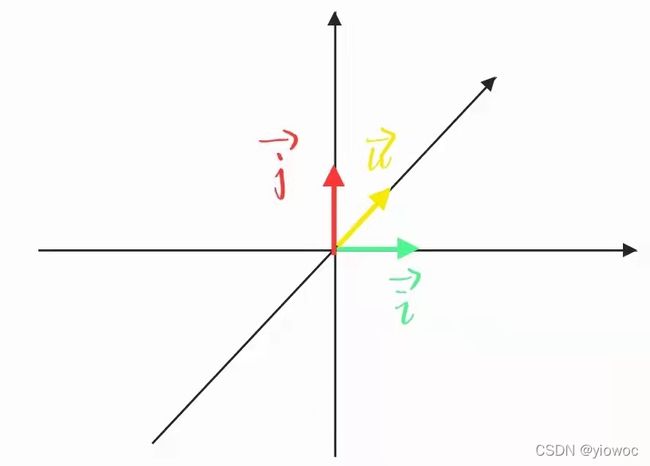
当把坐标看作标量的时候，基向量实际上就是这些标量缩放的对象

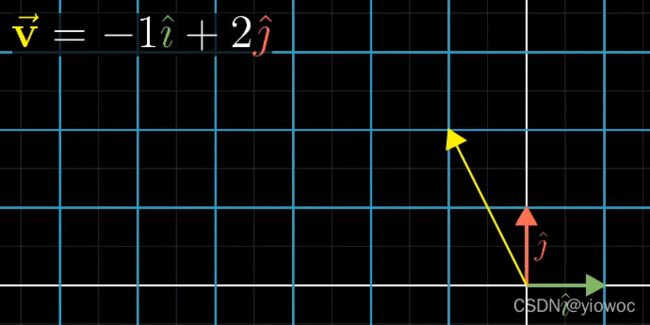
而向量就是由其中的每一位数【如Vi、Vj等，称为标量】将对应轴上的单位向量拉伸、相加后的产物

**当我们用数字描述向量时，它都依赖于我们正在使用的基。**因此，当我们使用其他的向量来作为该坐标的基，其标量会完全不同

给定向量张成的空间

基向量一共有三种情况：

• 两个向量不共线，它可以表示平面上的所有向量
• 两个向量共线，它只能表示平面一条直线上的向量
• 两个向量都为零向量，它只能表示零向量

而所有可以表示为给定向量线性组合的向量的集合被称为给定向量张成的空间，也可以理解为在仅使用向量加法和向量数乘的情况下，你能获得的所有可能向量的集合是什么

当基中的一组向量中至少有一个是多余的，没有对张成空间做出任何贡献，在这种情况下，我们称它们是“线性相关”的
$$u=av+bw$$
反之，则是线性无关的
$$u\ne av+bw$$

3-矩阵与线性变换

线性变换

“变换”暗示我们用运动的眼光去看待线性变换，严格意义上说，线性变换是将向量作为输入和输出的一类函数。我们可以把其看作从一个变量变换（平移、旋转、弯曲）到另一个变量。而线性代数则将变换条件进一步限制【保持网格线平行且等距分布，且原点位置不变】

而在线性变换的条件下，向量的变换有一个特点：变换前的向量，变换以后等于变换之后的基向量对于原向量标量的拉伸之和

而且当我们记录了变换后的基向量，就可以推断出任意向量在变换之后的位置

而当我们用计算来描述这个过程的时候，可以用如下形式：
$$Av=w$$
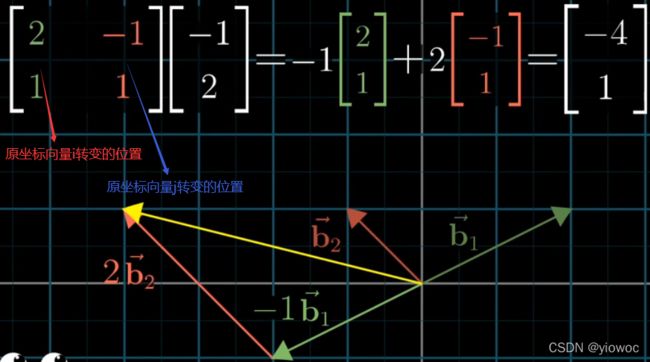
例：如果你有一个描述线性变换的2*2矩阵，以及一个给定向量，你想了解线性变换对这个向量的作用

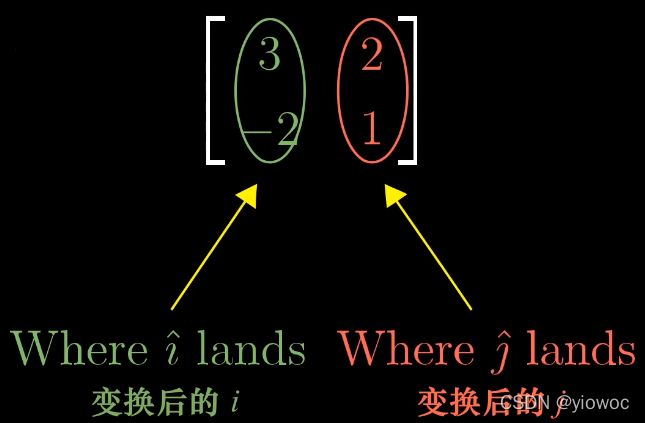
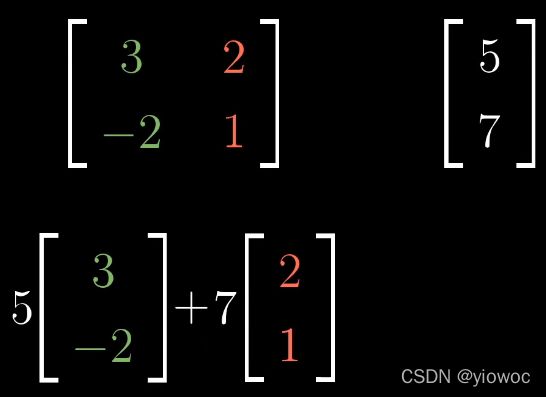
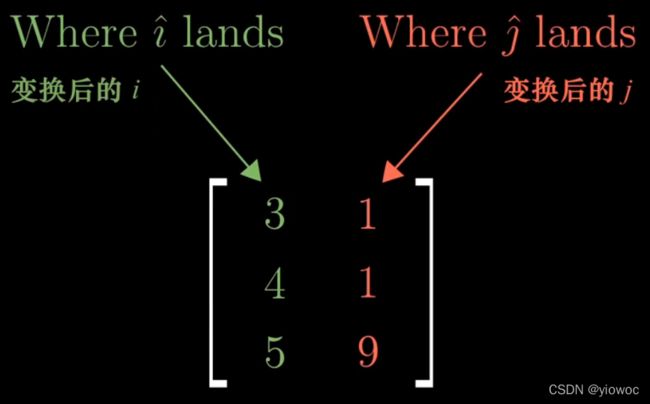
这里把矩阵的列看作是变换后的基向量

你只需要取出向量的坐标，将它们分别于矩阵特定列相乘，然后将结果相加即可

从运动的角度来看，即将hat(i)旋转，拉伸到(3,-2)，将hat(j)变化到(2,1)

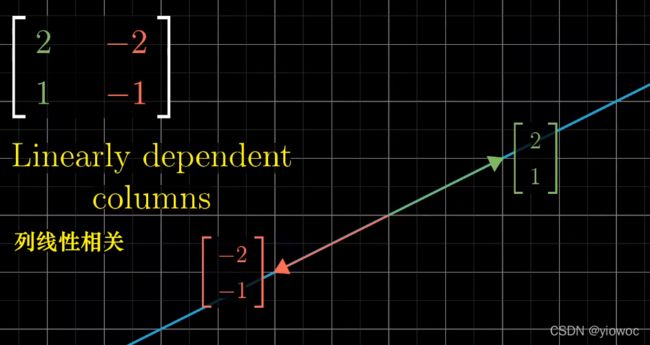
如果此时矩阵的两列线性相关，即hat(i)、hat(j)变换到了同一条直线上

总结

线性变换就是保持网格线平行且等距分布且原点不变的变换，而描述这种变换只需要几个数字，即变换后基向量的坐标，以这些坐标为列所构成的矩阵为我们提供了一种描述线性变换的语言，而矩阵向量乘法就是计算线性变换作用于给定向量的一种途径

矩阵代表一个特定的线性变换

4-矩阵乘法与线性变换复合

试想一种场景：

你想将一个向量进行旋转和剪切（两者皆为线性变换），此时你有两种方法

• 先将向量进行旋转，再进行剪切
• 两种变换同时进行（线性变换复合）

而此时两种变换同时进行的复合变换仍为线性变换（满足线性变换的特点），所以可以得出结论：

两个矩阵相乘有着几何意义，也就是两个线性变换相继作用

从公式来看矩阵乘法：

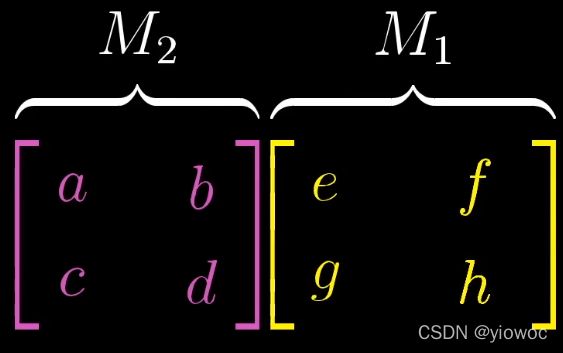
我们要考虑该矩阵乘法对向量到底产生了什么效果，就需要追踪M1，M2对hat(i)、hat(j)产生了什么变换

首先M1使得hat(i)变为(e,g)向量，而M2对(e,g)向量的操作即它对hat(i)的操作，所得最后的hat(i)为：

同理可得最后的hat(j)为：

此时该矩阵乘法对向量的变换就是使得向量的hat(i)、hat(j)变成了上述的hat(i)、hat(j)

所以请记住：两个矩阵相乘有着几何意义，也就是两个线性变换相继作用

附注1-三维空间中的线性变换

这个地方只是对线性变换的二维解释进行了扩展，这里不再赘述

5-行列式

线性变换改变原坐标的任意图形的面积（在二维空间中）的比例，被称为这个变换的行列式

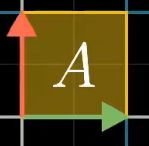
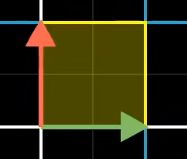
例子：观察原坐标(0,1,0,1)的正方形

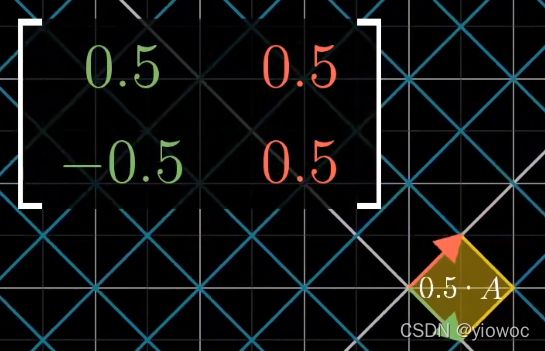
将其进行变换，变换后的面积为原面积的0.5倍

故该矩阵的行列式为0.5

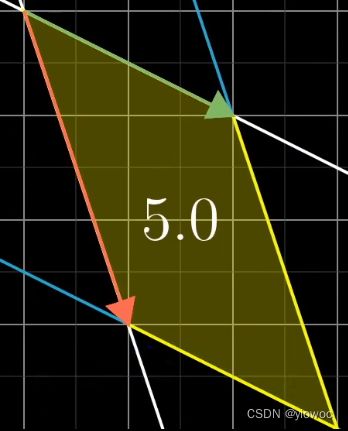
行列式的值可能为负数，可以理解为空间的定向发生了变化

如图，在下图情况下绿色箭头在右下方

经过变换后，红色箭头在绿色箭头的右下方，此时空间的定向发生变化，行列式为负数【个人觉得用右手定则更好理解】

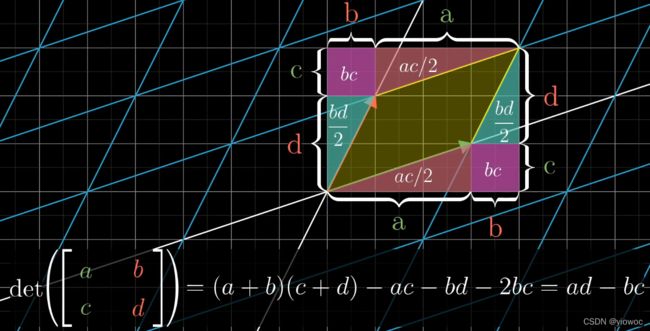
二维行列式计算推导

你可以用上述结论很简单的理解定理
$$det(M_1{M}_2)=det(M_1)det(M_2)$$

6-逆矩阵、列空间与零空间

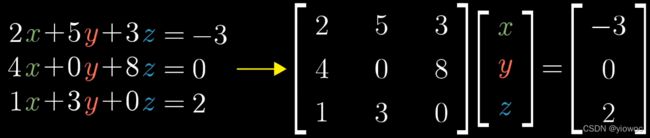
线性方程组

矩阵用途的广泛性可以体现在它可以用来求解特定的方程组，而且可以将所有的方程合并为一个向量方程，包含常数系数矩阵、未知量向量x、他们乘积得到的常数向量v

而这个问题可以从几何角度上理解：找出一个向量x，使得该向量与线性变换后的向量v相同

逆变换

我们可以通过逆向操作从向量v变换到向量x，而这一逆向操作也对应着一种线性变换，称为逆变换

通过几何理解我们可以知道A逆乘以A等于一个“什么都不做”的矩阵，而这种变换称为恒等变换，即保持每个基向量都不变

秩

当线性变换将空间挤压至降维的情况下（此时行列式为零），此时没有逆变换【你不能将一条线“解压缩”为一个平面】，此时行列式不一定无解，还可能有无穷多解

而线性变换将三维空间降维至平面或是直线的情况下，对于是否存在向量v使得算式成立所需的条件是不同的【直线情况显然比平面情况更加严格），此时可以引出“秩”的概念

“秩”代表着变换后空间的维数，更精确的定义为列空间的维数

列空间

对于三维空间上的线性变换，不管是一条直线、一个平面还是三维空间，所有可能的变换结果的集合称为矩阵的列空间，“列”字来源于矩阵的列，矩阵的列告诉你基向量变换后的位置，话句话说，列空间就是矩阵的列所张成的空间，也就是将矩阵的每一列作为基向量，这些向量张成的空间

零空间

零向量一定会被包含在列空间中（线性变换必须保持原点位置不变）

对一个满秩变换来说，唯一能在变换后落在原点的就是零向量自身。但是对一个非满秩的矩阵来说，它将空间压缩到一个更低的维度上，也就是说会有一系列向量在变换后成为零向量

举个例子，如果一个二维线性变换将空间压缩到一条直线上，那么沿某个不同方向直线上的所有向量就被压缩到原点；如果一个三维线性变换将空间压缩到一个平面上，同样也会有一整条线上的向量在变换后落在原点；如果一个三维线性变换将空间压缩到一条直线上，那么就有一整个平面上的向量在变换后落在原点

变换后落在原点的向量（即变换后一些向量落在零向量上）的集合，被称为矩阵的零空间

附注2-非方阵

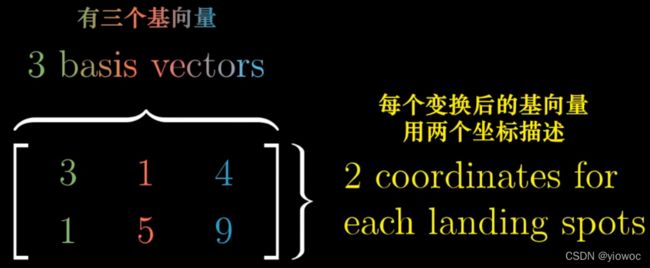
将几何理解扩充到非方阵中，非方阵的几何意义为将n维空间映射到m维空间上（n≠m）

如下图，即是将二维基向量映射到了三维空间中

而判断非方阵是否满秩可以判断其列空间的维数（张成空间的维数）与输入空间的维数（输入的列数）相等

所以非方阵与向量的乘法同样是对向量进行线性变换，只是变换后原空间的维度发生了变化

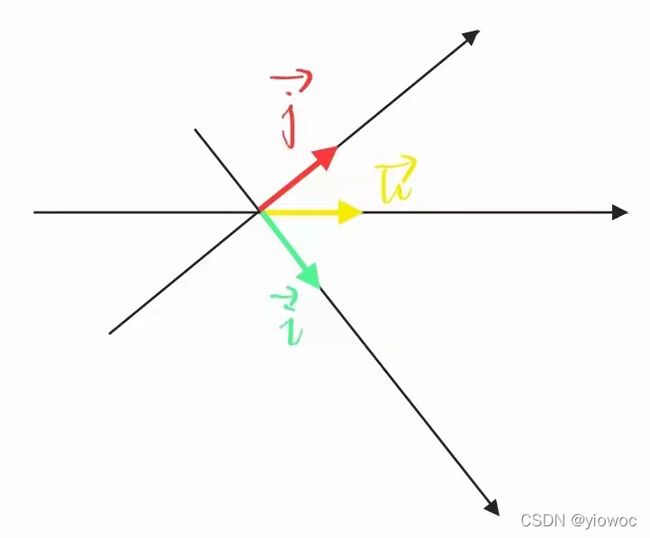
7-点积与对偶性

问题：

• 明明向量i在向量j的映射和向量j在向量i的映射是两个非常不同的操作，但是两者却都可以用来进行点积计算

当两个向量长度相等时，i对j以及j对i的映射互为镜像，所以即使操作不同，得到的结果是相同的

而当两个向量长度不同时，可以看作一个向量j被拉伸为原来的k倍，此时将i映射到j上，由于i没有变化，所以映射长度与j的长度之积为原来的点积的k倍；而将j映射到i上，通过三角形相似可以得出向量j在向量i上的投影也被拉伸为k倍，最后的结果为原来点积的k倍，所以这两种操作虽然方法不同，但结果是相同的

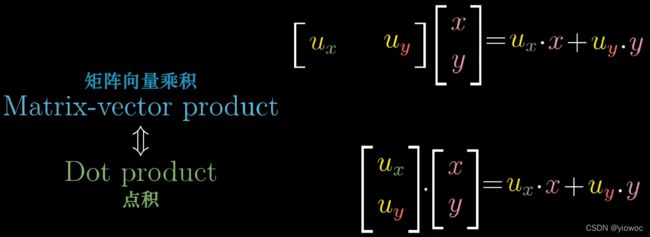
• 为什么点积计算（对应数相乘相加）和投影有关系——对偶性

首先，从视觉上看，一维矩阵与向量乘积的计算过程和两向量的点积一样，我们可以推测两者之间有微妙的联系【即将向量转换成数的线性变换和这个向量本身有着某种关系】

首先试想在二维平面内，定义过原点的不与x、y平行的一个轴u，有一个函数可以将任意向量映射到该轴上

通过视觉可知，当你有一系列结束点等距分布于一条直线上的向量应用于该函数，最后得到的向量的结束点同样等距分布在输出空间中，说明该函数为线性变换，我们可以通过求线性变换的方式去找出变换矩阵

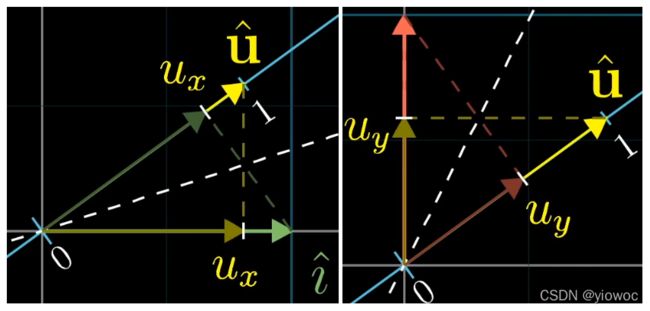
首先看这个图，我们要做的就是将两个基向量投影到u轴上的向量表示出来，用这种方式看起来可能有点麻烦，我们稍微旋转一下

由下图来看，当我们变换了坐标系，将向量i和向量j作为一个普通的长度为1的向量，那么这两个向量投影到u轴上的长度ux和uy为多少呢

根据对称性我们可以得到一个惊人的结论：向量i映射在向量u的长度等于向量u映射在向量i的长度；向量j同理

不用管向量i和j原来在旋转以后的坐标系的向量表示，向量i转化为一维数字ux，向量j转化为一位数字uy，则此时的变换矩阵就为：[ux,uy]，我们可以通过用该矩阵和任意向量相乘，得到一个映射在u轴上的向量

所以我们要求的变换矩阵满足一下特点：矩阵[ux,uy]恰恰为向量u在i、j坐标系下的向量表示（看上图），而该线性运算与点积的计算过程一摸一样，只是矩阵转换为一个向量，只是此时向量(ux,uy)为单位长度的矩阵

将单位向量(ux,uy)进行延伸（假设变为原来的k倍），使其成为一个非单位向量，此时ux、uy也被拉伸了k倍（可通过三角形相似证明），由于这些变换都是线性的，这就意味着新的矩阵向任何向量朝着u轴投影，并将结果乘以k倍

说到这里就可以证明了向量的点乘绝对值其实可以看作后面一个向量在前一个向量上的投影长度乘以该向量的长度，即一个多维空间的向量经过线性变换转换为一维的数字的过程，因为这个变换是线性的，所以它必然可以用某个1*n的矩阵描述，通过上述计算我们可以得出结论：这个多维向量转变为一维向量的线性变换，其实就是多维向量在线性变换矩阵对应向量上的映射

启发

你在任何时候看到一个线性变换其输出空间为一维数轴，无论它是如何定义的，空间中会存在唯一的向量v与之相关，就这一意义而言，应用变换和与向量v做点积是一样的，即一个多维空间到一维空间的线性变换的对偶是多维空间中的某个特定向量

8-叉积

8.1-叉积的标准介绍

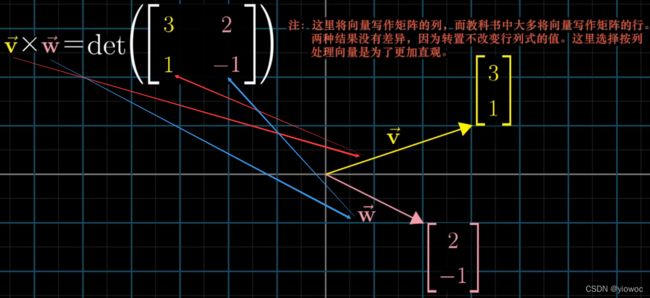
向量的叉乘的绝对值代表了两个向量构成的平行四边形的面积（与行列式相关）

叉乘结果的正负：可以通过右手法则来确定，从向量v到向量w，如果大拇指指向本人，说明为正；反之，为负

为什么该值为平行四边形的面积：由前面的知识可知：行列式的秩的值代表了原坐标系的任意一个图形在线性变换后的坐标系的面积变换的倍数；而秩的列表示了基向量的变化，由于线性变换指定的向量是默认的向量i、j，其构成的图形面积正好为1，所以该行列式的秩刚好为平行四边形的面积
$$de{t}_{parallelogram}\ast S_{square}=de{t}_{parallelogram}\ast 1=S_{parallelogram}$$
严格意义上讲，上述并不是向量的叉积：真正的叉积是通过两个三维向量生成一个新的三维向量，其方向通过右手定则决定，其大小等于两个向量构成的平行四边形的面积，而叉乘可以由下列式子计算出来

8.2-以线性变换的眼光看叉积

首先明确这一p视频解决的什么问题：如何将叉积的计算过程与几何解释相关联

叉乘的几何解释

两个三维向量叉乘生成一个新的三维向量，大小等于两个向量构成的平行四边形的面积

现有的疑问

为什么当行列式的第一列为基向量，二三列为叉乘的三维向量时，得到的是叉乘结果

关联证明

首先将第一列的基向量换为变量(x,y,z)，此时我们有一个从三维空间到数轴的函数了（与点积知识相关联）

由于该函数是线性的（线性变换，由于向量v，w固定，所以平行四边形面积不变，行列式的值与(x,y,z)线性相关），且是从三维空间到数轴的函数，所以我们可以用向量(x,y,z)与一个未知向量p的点积来描述这一过程

此时看等式右边的行列式，由于三阶行列式的值可以看作三个向量构成的图形的体积，向量v和w已知，所以平行四边形固定，向量(x,y,z)则提供了该向量在垂直于平行四边形的方向上的投影大小

换句话说，这个线性函数对于给定向量(x,y,z)的作用，是将这个向量投影到垂直于v、w的直线上，然后将投影长度与v、w张成的平行四边形的面积相乘，所以向量p也应该做到这些功能

这又与等式左侧相关联：点积的几何意义是向量(x,y,z)投影在向量p的值乘以p的大小，再通过上文可以推测向量p的方向与与平行四边形垂直的向量相同，且大小为平行四边形的面积

此时已经很清晰了，为了算出叉乘我们应该如何确定(x,y,z)的取值呢？

由于点积的结果是一个数，而非三维向量，当将(x,y,z)赋值为基向量时，经过点积后的结果仍为向量，且大小方向不变，此时得到叉乘的结果

所以叉积的计算过程与几何解释关联起来了

9-基变换

该p视频从另外一个角度带我们了解了矩阵在乘法中的意义（坐标变换、线性变换）

向量的表示依赖于我们对于基向量的选择，在平常我们使用的基向量i、j如下所示

我们可以选择不同的基向量

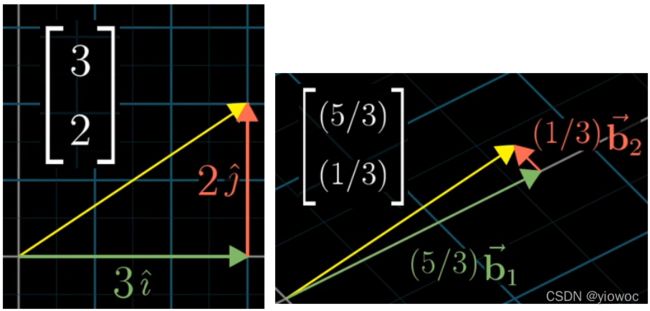
当我们使用不同的基向量时，我们描述同一条向量的数据描述就完全不同了（下图中的表示的向量完全相同）

我们可以用一个矩阵来进行两个坐标系的变换，而这种变换就是原来提到的线性变换

随之而来其他几个问题：如何计算从现在的坐标系到原来坐标系的变换矩阵？知道一个向量在老坐标系中的表示，如何在新坐标系中标识出来呢。。。解决这些问题需要分清楚向量是位于哪一个坐标系下的

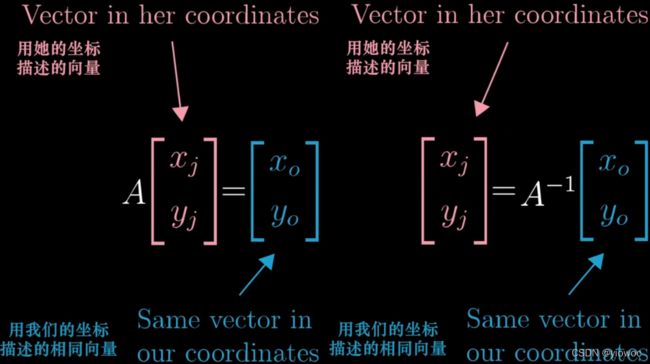
刚才求出的矩阵A的列代表的时新的坐标系的基向量，但是用原坐标来描述

而矩阵A与向量v的乘法，则是用原坐标系的向量来描述在新坐标系下的该向量的表述，所以矩阵A的作用是将向量v从新坐标系变换到老坐标系

反之，矩阵A的逆的列代表了老坐标系的基向量，通过新坐标来描述

而A逆与向量v的乘法，则是用新坐标的向量来描述老坐标系下该向量的表述

所以我们要在原坐标系下观察新坐标系下向量v的表示用Av计算，在新坐标系下观察老坐标系下的向量v的表示用A逆v计算

我们了解这些有什么用呢？下面的例子说明这个问题：

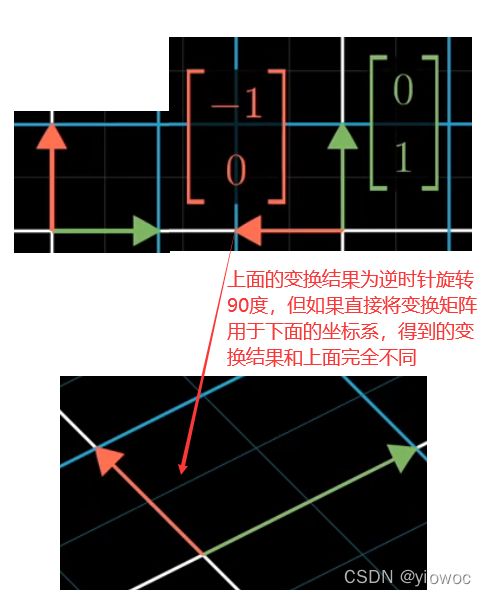
当我们知道在老坐标系下的a变换A，我们想在新坐标系下的向量v进行a变换，直接乘以A是错误的，因为矩阵A是根据老坐标系下的i帽和j帽来变换的，如果直接改变新坐标系下的i帽和j帽，得到的不是我们想要的变换

我们需要首先通过老坐标系的描述B来描述新坐标系，此时的i帽和j帽和矩阵A匹配，此时才能进行线性变换A，变换后的新坐标系仍然是用老坐标系来描述的，需要通过B逆改变回来，所以最后的公式为：
$$B^{-1}ABv$$

10-特征向量与特征值

首先我们来简单回顾一下特征向量的公式：
$$Av=\lambda v$$
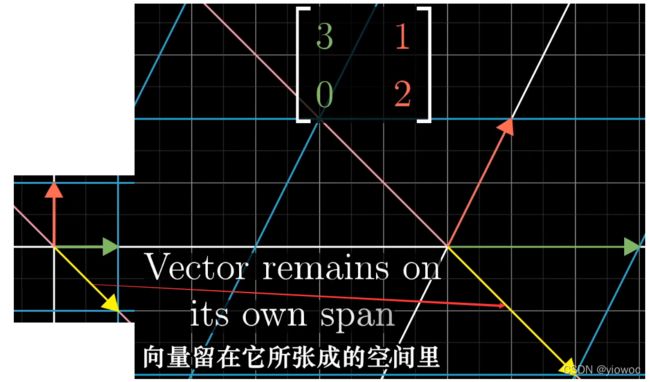
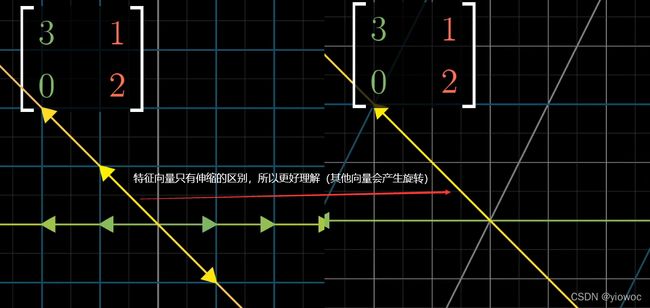
通过前面几章的学习我们可以了解到，特征向量本质上就是在坐标系变换后仍然在处于原来张成的空间中（也就是仅仅拉伸，但没有旋转）的向量，而特征值为该向量拉伸的倍数λ

并不是所有的线性变换都有特征向量，如旋转操作，如果有，特征向量的数量也是不定的

对于任一矩阵描述的线性变换，你可以通过将矩阵的列看作变换后的基向量来理解，但理解线性变换作用的关键往往较少依赖于你的特定坐标系，更好的方法是求出它的特征向量和特征值

特征向量和特征值的求法

这里仅仅简要的说明，将特征向量的公式移至一边
$$Av-\lambda v=(A-\lambda I)v=0$$
由于向量v可能为非零向量，只有当行列式A-λI为0时，A-λI与非零向量的乘积可能为零向量（这里简单解释一下，以二维空间为例，当A-λI行列式不为零，说明该变换矩阵线性无关，说明i帽和j帽一定不在一条线上，而线性变换后的非零向量v一定仍然不为零向量）。因此计算
$$det(A-\lambda I)=0$$
通常通过该算式得出的λ还需要带入原公式进行检验，检验过程省略

注意事项：虽然特征向量之间是线性无关的，但特征值可以是相同的（比如将i帽j帽拉伸同样倍数的变换）

特征基

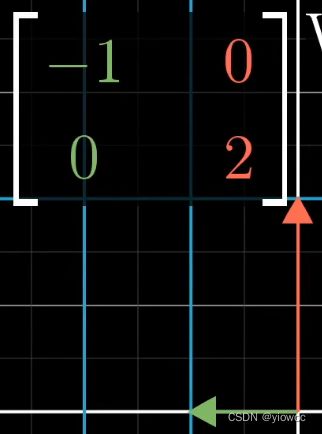
当基向量都是特征向量时，从几何上：基向量被不同程度的拉伸，但没有被旋转；从数据上：只有对角线上的数不为0【为对角矩阵】

对角矩阵在很多方面都更容易处理，其中一个更重要的方面是矩阵与自己多次相乘的结果更容易计算

当我们去计算非对角矩阵的100次幂时，计算复杂度会直线上升

此时如果你的变换有足够的特征向量能使你选出一个张成全空间的集合，那么你就能变换你的坐标系，使得这些特征向量就是基向量（通过基变换），此时你的特征变量都是基变量，所以变换矩阵一定为对角矩阵

11-抽象向量空间

具有向量特性的东西——函数

从某种意义上讲，函数实际上是另一种向量

• 两个函数相加——类比两个向量相加
• 函数和实数相乘——类比向量数乘
• 以空间中的箭头为背景考虑的线性代数的合理概念和解决问题的手段应该都可以应用于函数中
  • 线性变换、零空间、点积、所有特征的东西
    • 举例：线性变换为例，变换接受一个函数，并把它变成另一个函数（如导数）
    • 线性变换的严格定义：可加性、成比例

矩阵描述求导

首先确定基向量

在这个坐标系中，求导是用一个无限阶矩阵描述的，除了次对角线上按序排列正整数其他都为零

示例

线性代数中的很多概念在函数世界中都有直接的类比

所以，向量到底是什么

数学中有很多类似向量的事物，只要你处理的对象具有合理的数乘和相加概念，线性代数中所有关于向量、线性变换和其他的概念都应该适用于它

当我们要创建这么一个向量空间的时候，我们需要建立一系列向量加法和数乘必须遵守的规则（公理）

当你的向量空间遵守了这些公理，你就可以在上面应用线性代数的结论

因此，向量是什么形式不重要，重要的是它组成的空间只要满足上述公理即可

12-克莱姆法则、几何解释

线性方程组

形式：未知数和方程个数一样

目标：求出线性变换之前的向量值

方法

已知向量是矩阵列向量的线性组合

问题：结果取决于矩阵变换是否降维，在降维情况下，要么没有输入向量可以得到给定输出，要么有无数输入向量可以得到给定输出

引出想法

由于未知向量与基向量的点乘可以一次得出未知的值（x、y），那么进行线性变换后的两个向量是否仍然满足这个条件呢——答案是不满足条件（可以找出个例解释）

但这种想法给我们启发：有没有一种对输出向量的几何解释可以在矩阵变换前后保持不变呢

克莱姆法则

以二维空间为例，在二维空间中，未知向量(x,y)与基向量构成的平行四边形的面积在变换前后满足一定条件
$$S_{paral\_before}=det(D_{paral})\ast S_{paral\_after}$$

根据这个公式可以得到下面的式子

同理可得出x的值

三维空间与二维空间的做法几乎没有区别，只是输出变量的几何解释有平行四边形的体积变成了平行六面体的体积

整个课程到此结束，完结撒花！！！