线性代数-矩阵分解(Matrix Factorization)

$A=LU$（LU分解）
$A=QR$（QR分解）
$A=X\Lambda X^{-1}$ （谱分解）
$S=Q\Lambda Q^T$ (正交对角化)
$A=U\Sigma V^T$（奇异值分解)

1 LU分解

LU分解实际上就是 高斯消元法(Gaussian Elimination) 的矩阵表现形式，其中L指的是下三角矩阵(lower triangular matrix)，U指的是一个上三角矩阵(upper triangular matrix)。

---

2 QR分解

QR分解将一个矩阵A，分解成一个正交矩阵Q与上三角矩阵R相乘的形式。可以通过Gram-Schmidt方法构造，先通过Gram-Schmidt构造出正交矩阵Q，然后$R=Q^{T}A$，得到R。

---

3 谱分解(Spectral Decomposition)

所谓的 谱(spectrum) 就是一个矩阵 特征值(eigenvalue) 的集合。那么特征值是什么？特征值是指一个矩阵将一个特殊的向量线性转换的程度，这个特殊的向量称之为特征向量(eigenvector) ，所以对于一个矩阵而言特征向量要比特征值重要一些。

3.1 特征值和特征向量

这里详细分析一下特征值和特征向量。首先从定义来看一下:

给定一个 的矩阵$A$ ，$x$是非零向量，若存在一个数使$Ax=\lambda x$ 成立，那么我们称$\lambda$ 为矩阵$A$的特征值，称$x$为对应于$\lambda$的特征向量。

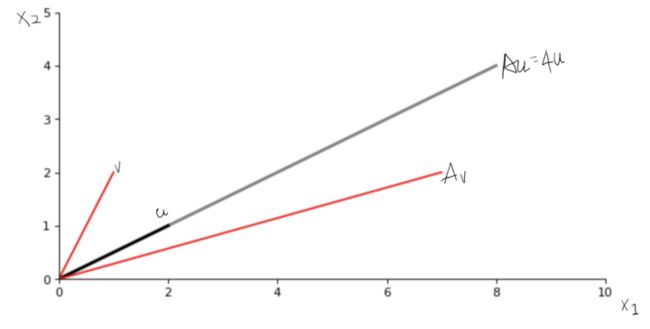
举个简单的例子，设$A=\left(\begin{array}{cc}3& 2\\ 2& 0\end{array}\right)$，可以验证$u=\left(\begin{array}{c}2\\ 1\end{array}\right)$是对应$\lambda =4$的特征向量，而$v=\left(\begin{array}{c}1\\ 2\end{array}\right)$不是$A$的特征向量，即$Au=\left(\begin{array}{cc}3& 2\\ 2& 0\end{array}\right)\left(\begin{array}{c}2\\ 1\end{array}\right)=\left(\begin{array}{c}8\\ 4\end{array}\right)=4u$成立，而$Av=\left(\begin{array}{cc}3& 2\\ 2& 0\end{array}\right)\left(\begin{array}{c}1\\ 2\end{array}\right)=\left(\begin{array}{c}7\\ 2\end{array}\right)$ ，找不到一个$\lambda$使得等式$Av=\lambda v$成立。

我们怎么理解这个等式呢，先看左边的向量，所以左边乘法的结果必然是还一个$n\times 1$ 的向量，也就是说一个$n\times 1$的向量左乘一个$n\times n$的方阵的结果依然在这个${\mathbb{R}}^n$ 的向量空间内。接下来我们看一下等式的右边， $4u$ 相当于对$u$线性的“拉长”了，却并未更改方向。这样我们就能够对特征向量有个直观的认识了，就是对于方阵 $A$ 而言，在${\mathbb{R}}^n$ 的向量空间内有些特殊的向量，这些向量能够在左乘$A$ 之后，只做线性大小的伸缩，而方向上不做改变。站在矩阵$A$ 的视角看，这种向量非常的特殊，针对A而言是独特的，因此我们给它起了个名字叫做特征向量。

借助下面的图我们可以直观的感受一下线性转换(linear tranfromation)，可以看出$Au$ 同 $u$ 的方向是一致的，而$Av$ 的方向却与 $v$ 不同。

3.2 谱分解

考虑一个 $n\times n$ 的矩阵 $A$ ，令 $A$ 的特征向量构成的矩阵为 $X=[x_1,x_2,...,x_n]$ ，
与 $X$ 中特征向量对应的特征值构成的对角矩阵为$\Lambda =\left(\begin{array}{cccc}{\lambda }_1& 0& ...& 0\\ 0& {\lambda }_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_n\end{array}\right)$，则有等式 $AX=X\Lambda$ 成立，下面检验一下：

$$AX=A[x_1,x_2,...,x_n]=[A{x}_1,A{x}_2,...,A{x}_n]=[{\lambda }_1{x}_1,{\lambda }_2{x}_2,...,{\lambda }_n{x}_n]=[x_1,x_2,...,x_n]\left(\begin{array}{cccc}{\lambda }_1& 0& ...& 0\\ 0& {\lambda }_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_n\end{array}\right)=X\Lambda$$

如果X 可逆(invertible) 的话，即$X$ 的列向量线性无关(linearly independent)，上式可化简为$A=X\Lambda X^{-1}$。

也就是说对于方阵A ，能够对其谱分解的前提是 $A$ 有 $n$ 个线性无关的特征向量，这样它们构成的矩阵 $X$ 才是一个可逆矩阵(invertible matrix)。

再考虑矩阵向量乘法，如果已知$Ax=\lambda x$ ，如何求$A^{n}x$ :

$$A^{n}x=A^{n-1}(Ax)=A^{n-1}(\lambda x)=\lambda A^{n-1}x=...={\lambda }^{n}x$$

几何上可以理解使用 $A$对 $n$ 次的线性转换，每次使$x$ 变成自身的$\lambda$ 倍。

---

4 对称矩阵的正交对角化

对称矩阵(symmetric matrix)，即 $S^T=S$，下面首先给出，对称矩阵的谱定理(the Spectral Theorem):

一个对称的 $n\times n$ 矩阵 $S$ 具有下面性质：

1. $S$ 有 $n$ 个实数(real)特征值，包含重复的特征值
2. 对于每一个特征值，对应特征子空间的维数等于作为特征方程的重数
3. 特征空间相互正交，这种正交性是在特征向量对应不同特征值的意义下成立的
4. $S$ 可正交对角化(orthogonal diagonalization)。

由于对称矩阵有 $n$ 个正交的特征向量，用$Q=[q_1,q_2,...,q_n]$ 表示 $n$ 个相互正交的特征向量组成的正交矩阵(orthogonal marrix)，对称矩阵 $S$ 可以谱分解成 $S=Q\Lambda Q^{-1}$ ，又因为 $Q$ 是正交矩阵，即 $Q{Q}^T=I$ ，即$Q^T=Q^{-1}$ ，$S=Q\Lambda Q^T$ ，所以将矩阵的逆替换成矩阵的转置使得对称矩阵的分解更加简单。

$Q$ 是一个正交矩阵，可按列向量展开，$Q=[q_1,q_2,...,q_n]$ ，其中 $q_i\in {\mathbb{R}}_n,i=\{1,2,...,n\}$ 是**单位正交(orthonormal)**向量，即 $|q_i|=q_i^T{q}_i=1，q_i^T{q}_j=0,i\ne j$.

$\Lambda$ 是一个对角矩阵(diagonal matrix)，$\Lambda =\left(\begin{array}{cccc}{\lambda }_1& 0& ...& 0\\ 0& {\lambda }_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_n\end{array}\right)$

$Q^T$ 是$Q$ 的转置(transpose)，因为 $Q$ 是正交矩阵，所以 $Q^T=Q^{-1}$

我们展开一下$S=Q\Lambda Q^T$ :
$$\begin{array}{rl}S& =Q\Lambda Q^T\\ & =[q_1,q_2,...,q_n]\left(\begin{array}{cccc}{\lambda }_1& 0& ...& 0\\ 0& {\lambda }_2& ...& 0\\ ...& ...& ...& ...\\ 0& 0& ...& {\lambda }_n\end{array}\right)\left(\begin{array}{c}{q}_1^T\\ q_2^T\\ ...\\ q_n^T\end{array}\right)\\ & =[{\lambda }_1{q}_1,{\lambda }_2{q}_2,...,{\lambda }_n{q}_n]\left(\begin{array}{c}{q}_1^T\\ q_2^T\\ ...\\ q_n^T\end{array}\right)\\ & ={\lambda }_1{q}_1{q}_1^T+{\lambda }_2{q}_2{q}_2^T+...+{\lambda }_n{q}_n{q}_n^T\end{array}$$

左右等式同乘一个$S{q}_1={\lambda }_1{q}_1{q}_1^T{q}_1+{\lambda }_2{q}_2{q}_2^T{q}_1+...+{\lambda }_{1}n{q}_n{q}_n^T{q}_1$ ，

因为$q_i$是单位正交向量，$q_1^T{q}_1=1$ ，$q_i^T{q}_1=0,i\ne 1$ ，

所以上式化简为 $S{q}_1={\lambda }_1{q}_1$ ，

同样方法可得表达式$S{q}_i={\lambda }_i{q}_i,i=\{1,2,...,n\}$，易见$S$ 对应特征值${\lambda }_i$ 的特征向量。

---

5 奇异值分解(Singular Value Decomposition, SVD)

不是所有矩阵都能分解成$A=X\Lambda X^{-1}$ 的样子，但是我们可以通过一个小的技巧实现对任意$m\times n$ 的矩阵分解成$A=U\Sigma V^T$ 的样子，这类分解称之为奇异值分解。

首先给出奇异值的定义，令$m\times n$ 的矩阵，我们可以通过$A^{T}A$来构造一个对称矩阵，这样就能够对其正交对角化了。( 因为$(A^{T}A{)}^T=A^{T}A$ ，所以它是一个对称矩阵)

有对称矩阵的谱定理知，$A^{T}A$ 对称矩阵有$n$ 个 单位正交(orthonormal) 的特征向量，且其特征值都是非负的实数，令特征值从大到小排列，则有${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_n\ge 0$ ，对应单位正交的特征向量分别为$q_1,q_2,...,q_n$ 。

考虑$||A{q}_i|{|}^2=(A{q}_i{)}^T(A{q}_i)=q_i^T{A}^{T}A{q}_i=q_i^T{\lambda }_i{q}_i={\lambda }_i{q}_i^T{q}_i={\lambda }_i$ ，

这里定义${\sigma }_i=||A{q}_i||=\sqrt{{\lambda }_i}$为矩阵$A$ 的奇异值，可见它是矩阵$A^{T}A$ 特征值的平方根，从几何角度理解，奇异值${\sigma }_i$ 就是向量$A{q}_i$ 的长度。

然后看两个对称矩阵，$A{A}^T$与$A^{T}A$，令$A{A}^T=U\Lambda U^T$，令$A^{T}A=V\Lambda V^T$，关于$A$的奇异值分解就要用到上述的两个正交矩阵: $U$和$V$，下面演示一下为什么$A$可以分解成$A=U\Sigma V^T$：
$$A^{T}A=V\Lambda V^T=V({\Sigma }^T\Sigma )V^T=V{\Sigma }^T(U{U}^T)\Sigma V^T=V{\Sigma }^{T}U{U}^T\Sigma V^T={(U^T\Sigma V^T)}^T{U}^T\Sigma V^T$$

由$A=U\Sigma V^T$，变换一下得$AV=U\Sigma$，展开如下(其中$r$为$A$的rank)：
$$\begin{array}{rl}& A\cdot v_1={\sigma }_1{u}_1\\ & A\cdot v_2={\sigma }_2{u}_2\\ & ......\\ & A\cdot v_r={\sigma }_r{u}_r\end{array}$$
相当于一系列的正交向量($V$)，在乘$A$后仍然还是正交向量($U$)。