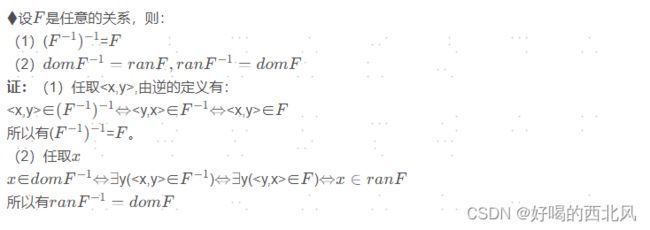【离散数学】二元关系

1、关系、关系矩阵、关系图

1.1 关系的定义

如果一个集合满足以下条件之一, 则称该集合为一个二元关系, 简称为关系，记作R.
（1）集合非空, 且它的元素都是有序对
（2）集合是空集

如∈R, 可记作 xRy；
实例：R={<1,2>,}, S={<1,2>,a,b}.
R是二元关系, 当a, b不是有序对时，S不是二元关系。

1.2 A上的二元关系

1.3 关系的类型

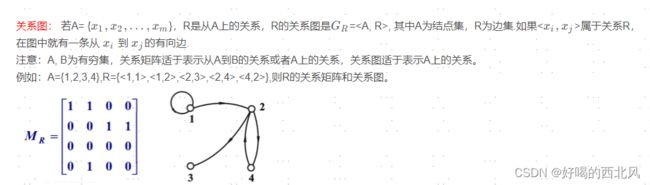
1.4 关系的表示

 

2 关系的运算 

2.1 定义域、 值域和 域,逆,复合

2.2 关系中的恒等式

 

2、关系的性质

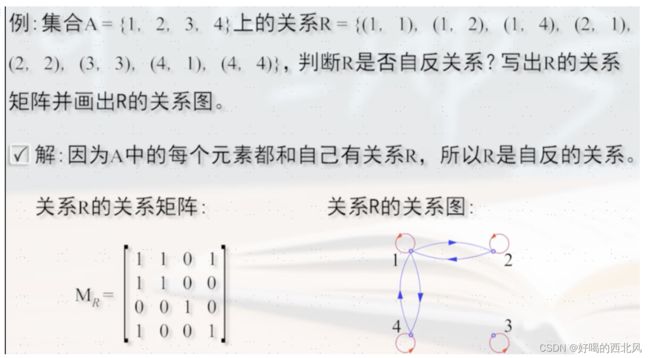
2.1 自反性

设R是集合A上的一个关系， 如果对A中的每一个元素x, 均有(x, x) ∈ R， 则称R是自反关系，即 R是自反的 ⇔ ∀x(x∈A →x, x) ∈R).

例如：正整数集合上的整除关系 (正整数总能被自己整除)， 相等关系等都是自反的关系。整数集合上的大于关系， 小于关系等都不是自反的关系。

分析： 由于(1,1), (2, 2), (3, 3), (4, 4) 都属于R,  所以是自反关系。

            每个元素都跟自身相关，关系图里都形成自环。

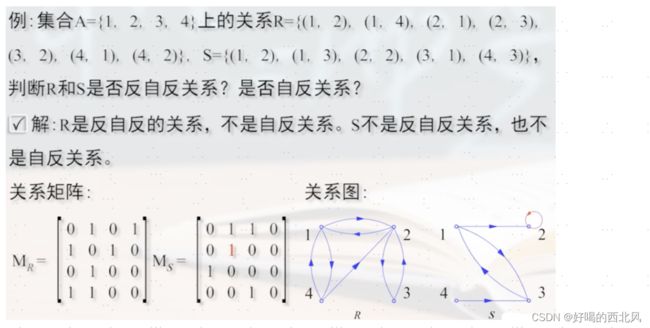
2.2 反自反关系

设R是集合A上的一个关系， 如果对A中的每一个元素x, 均有(x, x) ∉ R， 则称R是反自反关系，即 R是反自反的 ⇔ ∀x(x∈A →x, x) ∉ R).

例如：正整数集合上的大于关系， 小于关系等都是反自反的关系。整数集合上的整除关系， 大于等于关系等都不是反自反的关系。

看一个例子:

分析： S的关系图有一个自环，说明不是反自反关系， 又因为1，3，4 没有自环，所以不是自反关系。

总结：

1. 如果关系R是自反的， 则一定不是反自反的， 反之亦然。

2. 如果关系R不是自反的， 则不一定就是反自反的， 反之亦然。也就是存在既不是自反也不是反自反的关系。

3. 如果关系R是自反的，当且仅当R的关系图中每个结点都有环；如果关系R是反自反的，当且仅当R的关系图中每个结点都没有环。

4. 如果关系R是自反的， 当且仅当R的关系矩阵中主对角线上都为1, 如果关系R是反自反的， 当且仅当R的关系矩阵中主对角线上都为0.

2.3 对称关系

设R是集合A上的一个关系， 如果对A中的每一个元素x和元素y, 如有(x, y) ∈ R，必有(y, x)∈R, 则称R是对称关系，即 R是对称的 ⇔ ∀x∀y (x∈A ∧ y∈A ∧(x, y) ∈ R → (y, x) ∉ R)

例如：整数集合上的等于关系，任意集合上的全域关系， 同学关系，朋友关系等都是对称的。

2.4 反对称关系

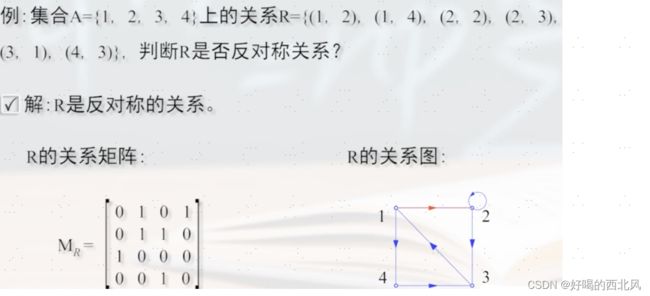
设R是集合A上的一个关系,如果对A中的每一个元素x和元素素y,若(x,y)ER和(y, X)ER, 就必须x=y,则称R是反对称关系,

分析： 这里除了(2, 2)之外，其他都不相等，所以是反对称关系

总结：

 对称性和反对称性的概念不是对立的，一个关系可以不具有对称性的同时也不具有反对称性， 且存在既对称也反对称的关系。

2.5 传递关系 

设R是集合A上的一个关系， x、y、z是A中的元素,  若(x,   y) ∈ R 和 (y, z) ∈ R,

必有(x , z) ∈ R,    则称R是传递关系，

例如：实数集合上的大于关系， 小于关系都是传递关系，同学关系、朋友关系等不一定是传递的。

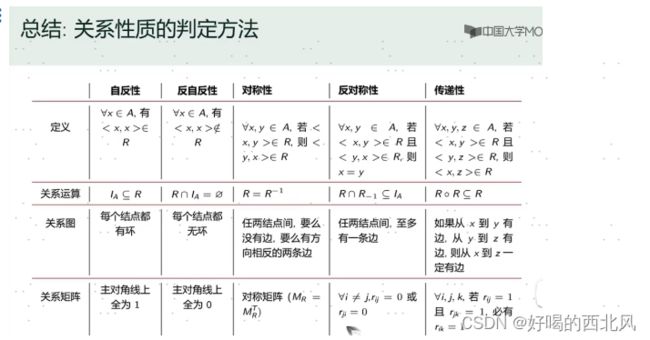
最后， 总结一下5种关系的特点，如下图所示

3、关系的闭包

1.如何在给定的关系中添加最少的元素使其具有需要特殊性质 --- 关系的闭包问题

2.让给定的关系具有反自反性和反对称性的方法与上面的方法是反过来的 --- 此时我们需要通过删除元素的方式来实现我们的目的

3.研究关系的闭包问题是有实际意义的：比如在程序中函数A调用函数B，函数B又调用函数C，此时函数C不具有传递性，通过函数C我们只能知道是函数B调用了它，但是实际上真正让函数C能够被调用的是间接调用它的函数A，有没有什么办法通过函数C直接获得函数A呢？ 答案是有的，我们通过给函数C添加最少的元素，使其具有传递性，这时函数A可以直接调用函数C，则我们就可以通过函数C得知真正调

用它的是谁了

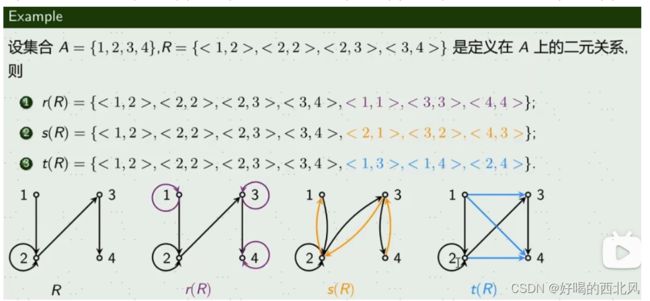
从上往下分别是自反闭包，对称闭包和传递闭包

4、等价关系与等价类

4.1 等价关系

定义：设R为非空集合上的关系。如果R是自反的、对称的和传递的，则称R为A上的等价关系。设R是一 个等价关系，若 ∈R ，称x等价于y，记作x~y。

（即R同时满足自反性、对称性、传递性，则R为A上的等价关系）

例题1

设A={1,2...,8}，如下定义A上的关系R：
R={|x,y≡∈A∧x≡y(mod3)}, 其中x≡y(mod3)叫做x与y模3相等（即x除以3的余数与y除以3的余数相等）

R={ <1,1>,<2,2>,<3,3>,<4,4>,<5,5>,<6,6>,<7,7>,<8,8>,   <1,4>,<1,7>,<4,1>,<4,7>,<7,1>,<7,4>,<2,5>,<2,8>,<5,2>,<5,8>,<8,2>,<8,5>,<3,6>,<6,3>}
因为∀x∈A,有x≡x(mod3)
∀x,y∈A,有x≡y(mod3),则有y≡x(mod3)
∀x,y,z∈A,有x≡y(mod3),y≡z(mod3)则有x≡z(mod3)
同时满足自反性、对称性、传递性，所以R为A上的等价关系
以下为R的关系图

例题2

设S={a,b,c},定义S上的关系R=Is∪{,}，R是否是S上的等价关系？（注：Is中的s为I的下标）

正确答案：是

4.2 等价类

定义：设R为非空集合A上的等价关系, ∀x∈A，令[x]R = { y | y∈A∧xRy }
称 [x]R 为 x 关于R 的等价类, 简称为 x 的等价类, 简记为[x]。

例题3

求例1中等价关系的等价类。

等价类：
	[1]=[4]=[7]={1,4,7}
    [2]=[5]=[8]={2,5,8}
    [3]=[6]={3,6}

等价类的性质

设R是非空集合A上的等价关系, 则

(1) ∀x∈A, [x] 是A的非空子集

(2) ∀x, y∈A, 如果 x R y, 则 [x]=[y]

(3) ∀x, y∈A, 如果 xy, 则 [x]与[y]不交

A={ 1, 2, … , 8 }上模 3 等价关系的等价类：
 [1]=[4]=[7]={1,4,7}，      
 [2]=[5]=[8]={2,5,8}，      
 [3]=[6]={3,6}
      以上3 类两两不交；   
       {1,4,7}∪{2,5,8}∪{3,6} = {1,2, … ,8}

设S={a,b,c}，定义S上的等价关系R=Is∪{,}，
则[a]=？[b]=？[c]=？

[a]={a,b}
[b]={a,b}
[c]={c}

集合的划分

定义 设A为非空集合, 若A的子集族π(π ⊆ P(A)) 满足下面条件：
(1) Ø ∉ π

(2) ∀x∀y (x,y∈π∧x≠y→x∩y= Ø)

(3) ∪π=A

称π是A的一个划分, 称π中的元素为A的划分块。

例题

--javascripttypescriptbashsqljsonhtmlcssccppjavarubypythongorustmarkdown

设A＝{a, b, c, d}, 
给定π1,π2,π3,π4,π5,π6如下：
      π1= { {a, b, c}, {d} }，
      π2= { {a, b}, {c}, {d} }
      π3= { {a}, {a, b, c, d} },
      π4= { {a, b}, {c} }
      π5= { Ø,{a, b}, {c, d} }, 
      π6= { {a, {a}}, {b, c, d} }
  
π1,π2是A的划分，其他都不是A的划分。

商集

定义：设R为非空集合A上的等价关系, 以R的所有等价类作为元素的集合称为A关于R的商集, 记做A/R, A/R = { [x]R | x∈A }

--javascripttypescriptbashsqljsonhtmlcssccppjavarubypythongorustmarkdown

 A={1,2,…,8},A关于模3等价关系R的商集为：
      A/R = { {1,4,7}, {2,5,8}, {3,6} }
      A关于恒等关系和全域关系的商集为：
              A/IA = { {1},{2}, … ,{8}}
              A/EA = { {1, 2, … ,8} }

--javascripttypescriptbashsqljsonhtmlcssccppjavarubypythongorustmarkdown

设S={a,b,c}，定义S上的等价关系R=Is∪{,}，
则S/R=？

正确答案：{{a,b},{c}}

等价关系与划分的一一对应

例如： A={1,2,…,8},A关于模3等价关系R的商集为：
A/R = { {1,4,7}, {2,5,8}, {3,6} }，它就是Ａ的一个划分

不同的商集对应于不同的划分；

任给 A 的一个划分π, 如下定义 A 上的关系 R：

R = { | x,y∈A∧x 与 y 在π的同一划分块中}，则 R 为 A上的等价关系, 且该等价关系确定的商集是π。

例9：

求出A＝{1,2,3}上所有的等价关系
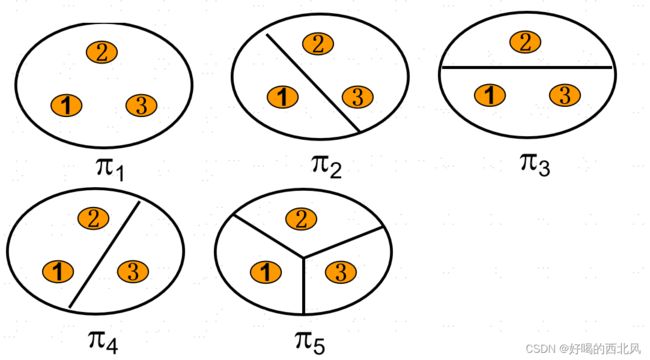
求解思路：先求出A的所有划分, 然后根据划分写出对应的等价关系。(如下图)

π1对应于全域关系 EA
π2对应等价关系 R2={<2,3>,<3,2>}∪IA
π3对应等价关系 R3 ={<1,3>,<3,1>}∪IA
π4对应等价关系 R4={<1,2>,<2,1>}∪IA
π5  对应于恒等关系 IA
(注：以上所出现的IA，A为I的下标)

 

5、单射、满射和双射的定义

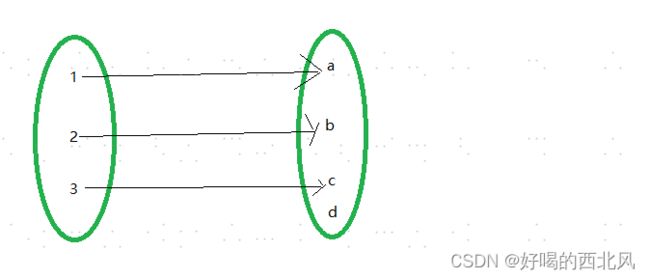
单射

一对一函数，x不同则y不同 （一个萝卜一个坑，可能有坑没有萝卜）

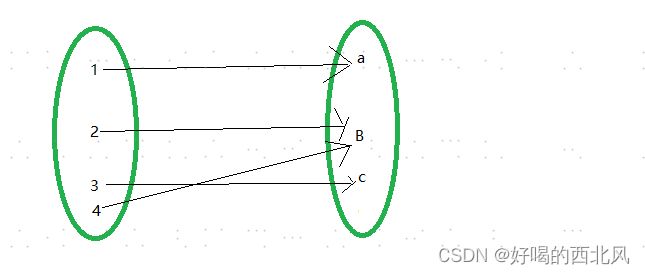
满射

值域y是满的，每个y都有x对应，不存在某个y没有x对应的情况 (满坑萝卜，可能有的坑，有多个萝卜)

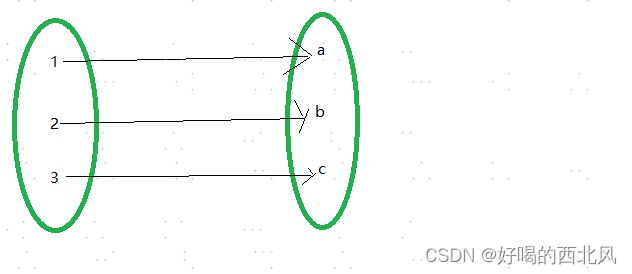
双射

每个y都有x对应，而且都是一一对应 （一个萝卜一个坑，所有的萝卜都有坑，所有的坑都有萝卜）

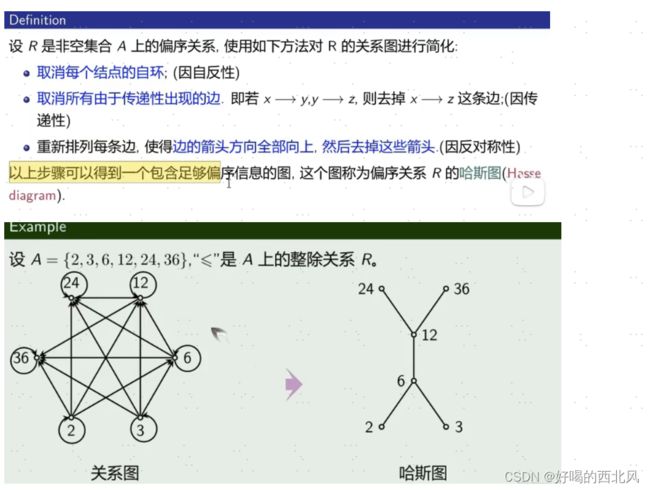
6、偏序关系与哈斯图

当我们用 ≤ 符号来表示偏序关系的时候，这个符号就不再局限于它本来的含义了，此时的它表示的是元素之间的先后顺序，如下图：

 

可比与覆盖

哈斯图

特殊元素

最大元和最小元

1. 

要注意的是集合中的最大元和最小元有且只有一个，如果找不到一个最大/最小元的话，则这个集合的最大/最小元为无

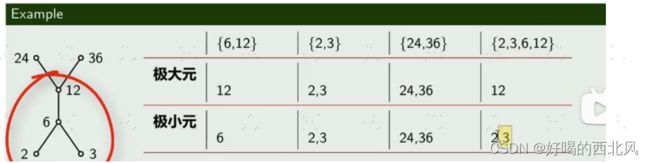
极大圆、极小圆

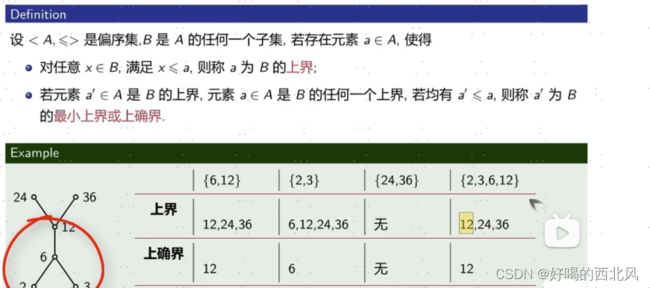
上界、上确界

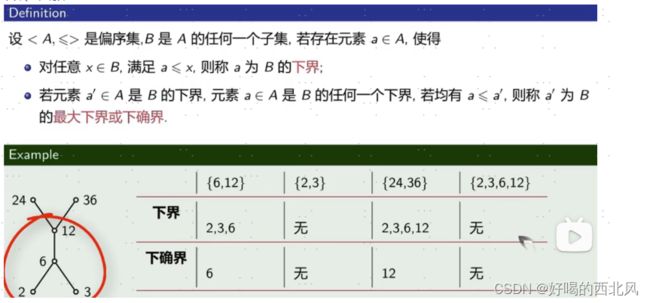
下界、下确界

1.下确界就是所有下界中最大的那个

2.对于一个集合而言下界和上界可以有很多个，但是它的下确界和上确界有且只有一个

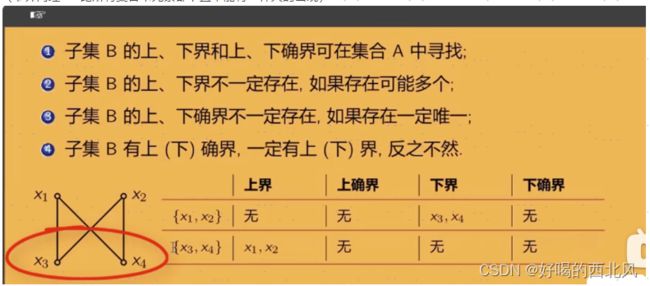
2.作为一个集合的上界的元素必须比集合中的所有元素都大（集合中不能够有一样大的元素出现），否则 的话这个元素不是集合的上界

（下界同理 --- 比所有集合中元素都下且不能有一样大的出现）