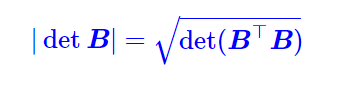线性代数几何直观的理解
这门课的重要性不言而言,它是解释线性代数的来源以及它可以怎么用的重点,而在学校里面,我们只能够学到它的定义和计算方式。
1 向量是什么?
1.1问题
- 向量是什么?
学物理的说是空间的一个箭头,学计算机的说是列表。而学数学的说,向量可以是任何东西,只需要满足向量加法和数乘的法则都可以叫向量。不过为了学了线性代数的几何,我们暂时认为它是箭头吧。
这和数学仅仅是一些数字和定义在其上的一些运算,多么相似。
- 向量的加法和数乘在坐标系中分别代表什么?(向量就这两种基本运算,点积,叉积都是在其为基础之上的)
比如v+w,在坐标系中表示先沿着v走一段路,再平移w走一段路,最后走到的地方就是和。
而数乘表示拉伸或者缩短向量。
这不禁让我想起概率图模型的理论原理是如此简单。
2 线性组合、张成的空间和基
- 基向量是什么?
当我们把一个向量当成标量的时候,那么它的数值(坐标系位置)就是对基向量的缩放得到。比如仅仅依靠二维空间中i和j基向量,我们就可以获得二维空间所有箭头(点)。
- 线性组合?
当我们书写av+bw,a,b是常数,v和w是向量。我们也可以获得一个结果向量,这个结果向量就是v和w经过线性组合得到的。
那么线性的意思是什么?如果固定a,而仅仅改变b那么结果向量就只能在一条直线上运动了。
经过v和w的线性组合(简单运用向量加和数乘法则),我们可以在二维空间获得所有的二维向量,那么所有二维向量组成的空间被称为给定向量张成的空间。扩展到三维也是一样的。(前提是v和w不共线)
这里需要记住:线性代数紧紧围绕向量的加法和数乘法则。
- 线性相关、线性无关
比如二维空间内,v和w共线,就是w落在v的空间(线)上。表示w对张成空间没啥贡献,它可以由v来描述。我们称v和w线性相关或者w可以写成v的线性组合。
如果v和w都对张成空间有贡献,每个都提供了一个维度,我们称v和w线性无关。
最后:向量空间的一组基是张成该空间的一个线性无关向量集。
3 矩阵和线性变换
考虑上图中的v=-1i+2j,其中i和j都是经过最原始的[1,0]和[0,1]变换之后的基向量,所以我们想要知道变换之后的i和j的线性组合得到v。其中变换后的i和j都是二维的基了,而它们变换的对象就是[-1,2],这是一个二维空间转二维空间的变换,所变换的[-1,2]就会在其变换后的地方找自己会在哪里。
4 矩阵乘法与线性变换复合
在这个图上,[x,y]先经过旋转矩阵,然后再经过剪切矩阵,这两个变换可以合并成一个变换,也就是复合矩阵。两个矩阵相乘有几何意义,也就是两个线性变换相继作用。并且需要从右从左来作用。把剪切矩阵叫A,旋转矩阵叫B,我们发现Ax表示A对x进行线性表换,而得到的x对应的向量所在位置(一个点),那么AB呢?它表示B经过A的变换,得到自己各列对应向量所在位置(其实就是转换空间,两个点,但是原点是不变的)。Ax叫线性变换,AB叫线性复合变换。
- 那么AB和BA不可以交换也就可以理解了?
- 那么很自然的(AB)C=A(BC)也就很好理解,可以成立是因为其还是一步一步进行的。他很好的解释矩阵乘法具有结合性。
5 三维空间线性变换
考虑这个矩阵,其实我们有着隐含的假设就是原本的i,j,k都是单位向量,经过这个变换之后,i到了k轴的-1位置,j不变,k到了x轴的1位置,这就是一个三维空间基向量转换。
而要知道某个[x,y,z]变换后到了那里,就用[x,y,z]乘以该矩阵即可。
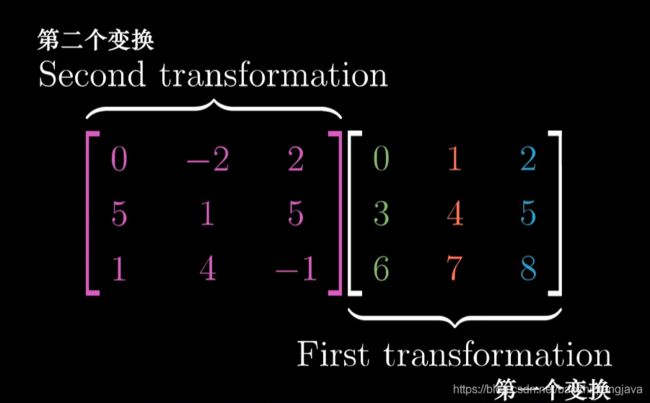
而两个三维矩阵乘积也就是两个变换,基变换。这里不涉及到把某个向量变换到某个点,你甚至可以理解为左边的第二个变换,把右边的三个点分别变换到了另三个点。
7 行列式
7.1 内容
- 行列式的值决定了该变换对空间的缩放比例。
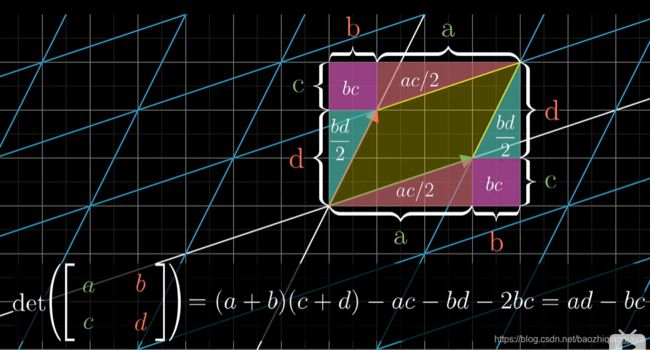
但是是为什么呢?是如何做到的呢?考虑一个最简单的例子
二维空间中的行列式的值等于上图中的黄色区域面积,这通过几何知识去得到的。也就是ad-bc的结果,这是计算二维行列式的便捷方法,但是一定要明白它的由来。
7.2 问题
7.2.1 为什么只有方阵有行列式?
首先回顾行列式的标准定义。
n维方阵的行列式的绝对值,等于它的各个行(或列)向量所张成的n维立体的超体积。
那么教材根本没有非方阵的计算方式,不过我们可以解除方阵的计算技巧来尝试给非方阵计算一个值。
可以参考这篇https://spaces.ac.cn/archives/2757给出的过程,给非方阵计算一个定义,而不是常规的定义。
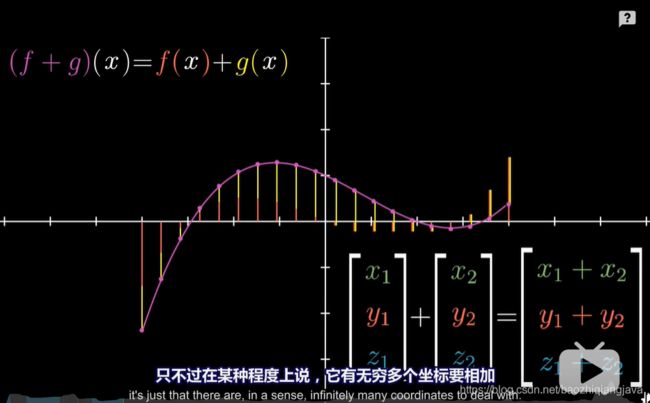
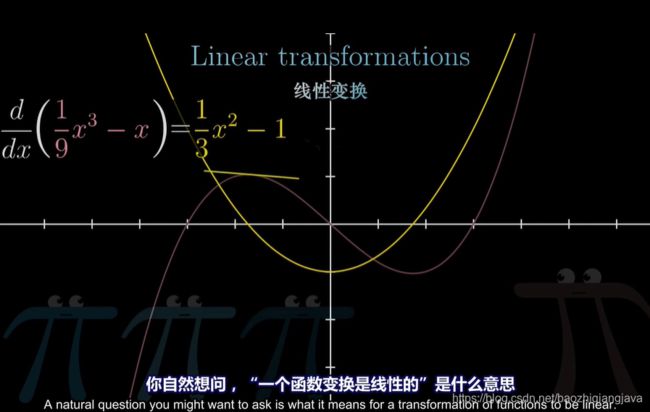
对于一个n*n方阵,直接有其计算公式。而对于n*k矩阵,当n>k时,其肯定张不成一个n维体,这样一来,它的n维体的超体积自然为0。但其还是可能有值得,比如n-1维的存在“体积”。而对于n 借助该公式,我们可以计算非方阵在n>k情况下的值,直观来说其还可以保留其几何意义(需要证明)。举个例子,对于n*2矩阵来说,行列式的几何意义就是平行四边形的面积,所以使用 而对于n 比如3*4矩阵,那么这个4就是其4列元素所张成的空间。 秩表示经过该矩阵线性变换之后的维度。满秩表示,还是原来列数目维度, 经过变换之后落在零向量的东西就是零空间,也就是Av=0的所有的解v。 它的几何意义就是把二维空间映射到三维空间上的一个过原点的平面,这样的线性变换是由两个向量决定的也就是列空间是二维,但整个3*2的矩阵表示的是三维空间中的一个二维平面。 这个矩阵有两列,表示初始由两个基向量描述,但是有3行,表明每个基向量变换之后由3个独立的坐标描述。但它仍然是满秩的,因为输入列空间和输出列空间是同等的。 那么对于一个2*3的矩阵来说,怎么办呢? 它表示原来空间有3个基向量,然后2列每个变换后的基向量用两个坐标描述。也就是三维空间变换成二维空间。 这是二维转三维空间,但是注意是基向量的变换。而整个矩阵表示的是三维空间中的一个过原点平面,所以如果这个矩阵为A,那么Ax=b,b肯定会在这个平面上。而矩阵A也是满秩的。 终于理解点积的几何意义了,首先点积是人们定义的某种运算,比如下图 但它同时又有几何意义,就是一个向量的长度乘以它在另一个向量上投影长度,所得就是点积结果。但是这个点积运算定义和几何意义是如何关联在一起的呢? 从向量的加法和数乘可以得到向量的乘法运算规则,但是我们发现,1*2的向量乘以2*1的向量得到结果和点积运算一样的。 那么是可以用向量乘法来解释点积运算的几何意义的。 首先向量乘法的本质是变换,也就是函数,而1*2的向量乘以2*1的向量会得到一个数,但是本质是跑不掉的,就是通过交换基向量实现变换,而这里,刚好,变换后的一维空间数轴中单位向量的横纵坐标恰好就是这个1*2向量中两个数,而2*1向量就当成函数的自变量x,得到它在数轴上的位置,刚好就需要矩阵变换(也就是向量乘法)得到。也就实现了一个2*1向量在另一个向量上(变换后数轴的单位向量)上的投影长度*该数轴单位向量长度,得到就是点积结果。 举个例子[1,0]*[3,4]T等于3,表示[3,4]T在[1,0]上的投影长度为3,这时候,[1,0]表示原来空间是二维的,现在变成一维的x数轴,y塌陷了,所以[3,4]T,只有投影长度=3了。3乘以单位向量长度1还是等于3。 如果[1,0],换成[1,2],那么就表示原来空间是二维的,现在变成一维的数轴,x,y都到了[1,2]向量箭头所成的数轴上。这个数轴的单位向量长度就是√5,那么[3,4]在其上的位置就是通过[1,2]*[3,4]T得到,也就是[3,4]T在[1,2]上的投影长度*[1,2]所代表数轴单位向量长度,可以验算的,是正确的。 利用的是对偶性,一个多维到一维空间的转换,恰好就是多维空间中的某一个向量。 如何从线性变换的角度理解叉积,可以有如下计划。 叉积还是没懂,对不起。 给出了两个拥有自己基向量的坐标系,如何对同一向量进行转换。就算变换,其原点还有坐标轴的等距分布都是一样的。 比如上图的二维向量就表示是我们把单位向量i,j变换基了。 举个例子,我们是单位向量i,j,用我们的语言描述詹妮弗的基向量就是左边的的矩阵,那么对于用她的坐标描述的向量,如何转换为用我们的坐标描述的相同变量呢? 直接用该矩阵,然后进行矩阵乘法。 上图就是 那用我们的坐标描述的向量,如何转换为用詹妮弗的坐标描述的向量呢?直接对矩阵求逆,然后进行矩阵乘法。 深入想一下,对于网络传播树中不同的的点来说。它可以拥有自己的坐标系,这个坐标系的维度就是其分支数目,那么刻画不同维度的分支所构成的(体积、或者面积、或者什么的)。 首先Ax=b,表示A对x进行线性变换,然后b是x经过变换基向量得到的向量。而Ax=mx,表示A对x进行线性变换后,只是对x进行伸缩而已。那么如果m存在,x表示的是A线性变换中不变的量(比如直线、旋转轴、),也叫特征向量,而特征值则表示对其伸缩的程度而已。比如二维向量A求其特征向量,就是求一条直线,该直线在线性变换只是伸缩而已。 向量是什么?我们看似用向量去理解线性变换,但是事实上,而行列式以及特征向量都跟你选择的坐标系无关。所有长的像向量并满足相加和数乘法则的一些数,都可以认为是向量的运算,也就是矩阵线性变化,比如求导这种事情也可以和线性变换一样的。求导是将一个函数(向量)经过求导(线性变换)变成另一个函数(向量)。 比如这里,两个函数的相加得到一个新函数也可以理解为两个向量的相加得到一个新向量,数乘也一样。那么在微积分中的求导跟矩阵变换有什么关系呢? 事实上,它也可以用矩阵变换来代替。那什么是线性变换呢? 那我们就可以理解,求导也是线性的。因为它满足可加和数乘法则,比如 那如何用矩阵描述求导呢? 这个图告诉我们答案了,某个多项式的求导是这里A对x的变换,其中基函数就是那么未知数之前的系数,我们在上图,我们完成了用矩阵线性变换进行求导的过程,只需要定义基函数以及找到A,多么神奇。很明显,其对幂函数不成立。 那么矩阵变换在数学中都有其描述。 本系列暂时结束,但是后续就靠《线性代数及其应用》续命。  得到。
得到。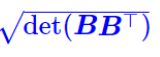 ,因为需要保留其几何意义。(这也是非方阵的没必要性,因为其对应的线性转换后的“体积”不是唯一的)再次参考该博客,可以得到(我们想要的一个解释)
,因为需要保留其几何意义。(这也是非方阵的没必要性,因为其对应的线性转换后的“体积”不是唯一的)再次参考该博客,可以得到(我们想要的一个解释)8 逆矩阵、列空间、秩、零空间
9 非方阵(不同维的空间转换)

10 点积的几何意义
11 叉积的几何意义
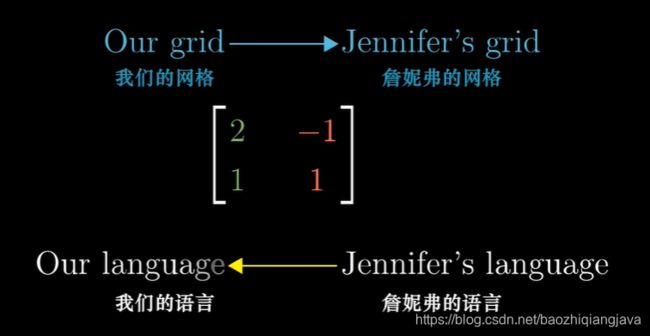
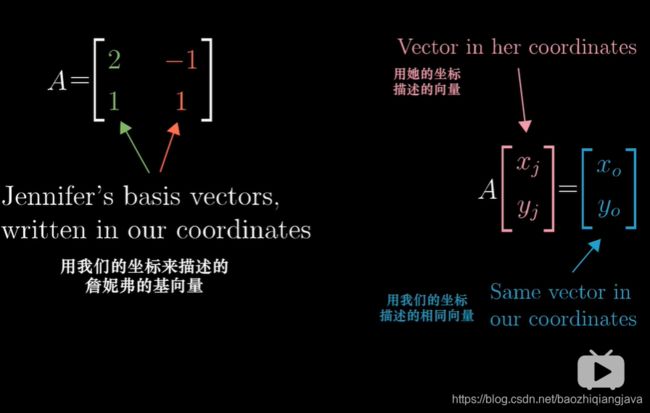
13 基变换
14 特征值和特征向量
14.1 问题
15 抽象向量空间