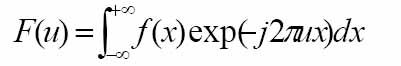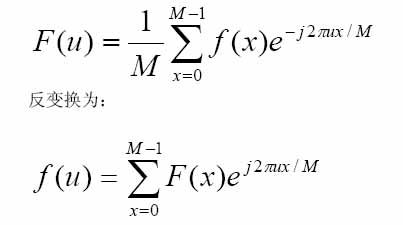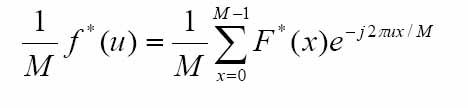第一次邂逅快速傅立叶变换(FFT)

【原文：http://blog.csdn.net/yin138/article/details/1571358】

为了毕业设计，我要学习JPEG，还有视频压缩技术，在JPEG的时候，我就被前面的DCT给挡住了，现如今我终于写了一个FFT程序，发了我好长的时间。如果说是因为我的无知，还是什么，我对学习这类有关数学的东西，总是显得那么的迟钝，也许是因为人老了吧。其它我还像个小孩子一样，唉，这年头，还真是搞不懂自己了。
进入正题吧，我对FFT的完全不了解，到最后，实现FFT正变换与反变换，其中有太多的细节，如果我现在能说明的，一定全力说明，以让与我一样对FFT这东西有点害怕，但又不得不理解的人来说，也许会有些用处。

首先，FFT（快速傅立叶变换）的作用是要是用于将一个有限数字信号从时间域转换到频率域。什么是时间域呢？简单的可以这样理解，就是一个信号是与时间相关的，用平面坐标来说就是横坐标是以时间t，纵坐标是时间t上的一个函数值f(x),我们叫这个函数f(x)为时间域。当一个信号经过FFT变换之后，将变成频率域。什么是频率域呢？同样可以这样理解，它其实就是一个用频率与相位来标识的一个函数。像F(x) = Asin(ωx+φ),在数学中A表示幅值，而ω表示频率，φ表示相位。我们假设F(x)一个频率域函数，那么其频率谱就是|F(x)| = [R^2(x)+I^2(x)]^(1/2),其中R与I表示取实部与虚部函数。需要说明的一点，那就是FFT变换是一个复数变换，所以F(x)是一个复数函数。

我们知道了时间域与频率域的概念之后，下一步就是为什么我们要使用时间域到频率域的转换呢？现在我也只知道其中的一点，那就是在JPEG中可以将数据的高频部分找出来，也就是相关性，这样方便数据压缩。总之一点，你学习这个东西，那么你一定是知道这东西可以用到你想做的东西上面。其实FFT代码在很多网站上都有源码，而且到处都有下载，如果说你想自己研究一下，学习一个这个东西是个啥样，那么我想那还是有必要看一下理论知识的。其实给你一个公式，如果你能马上写出其代码，那已经是很不错的了。我在学FFT的时候看到那个DCT（离散余弦变换）的公式，然后是一个很不知道来源的代码，还真不知道如何下手。呵呵，经过努力还是将FFT完成了。

FFT中理论知识有很多，我想要学会如何变换，知道其中一种就可以了，至于其它优化算法，那就要慢慢研究。FFT中快速算法的理论我们需要知道的就是“蝶形运算”。我给出一个图：

图1：蝶形运算N = 8时分解图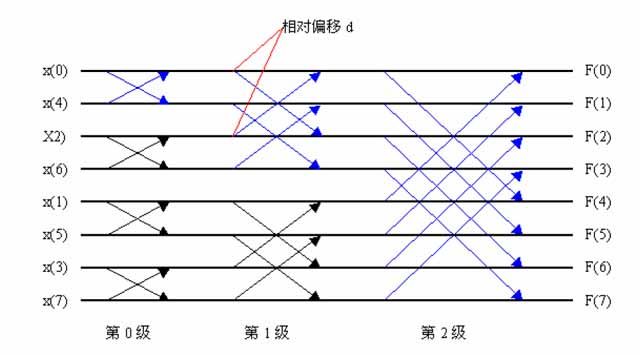

图2：蝶形运算公式

以上两个图在很多书上很讲解过，我也是画过来的。
我们知道以上的内容之后，还不能做什么东西，因为我们不知道为什么会呈现这样的一个图，所以下一步我们将给出几个公式。
一维傅里立叶变换公式
 
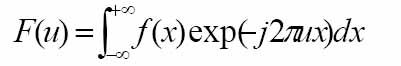
这个式子，是对连续信号处理的，在实际中我们是离散信号， 所以我使用离散处理的公式（为什么呢？原因之一我们原始信号是离散的，另外我们是处理有限域的）
离散公式为：

 

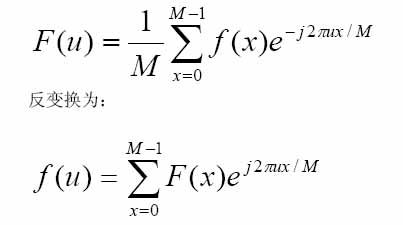
经过上面两式我们可以看出正变换与反变换有相似之处，我们对反变换的函数f(u)与F(x)取共轭复数（虚部取负就可以了）就可以得到与正变换相似的变换，这样我们就可以利用正变换得到反变换，在变换之前，我们需要取共轭复数，在变换之后，我们还要取共轭，然后再乘以M就可以得到反变换了。
 

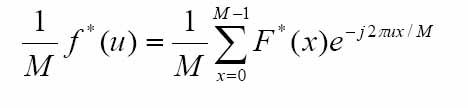
我们知道了公式之后，下一部就是如果将其变成蝶形运算来加快运算的速度。从公式中可以看出我们如果直接运算的话，运算量相当的大。为什么能进行蝶形运算呢？其实在很多书上都讲解了，我主要讲的是如何支实现，所以可以参考其它书籍。因为傅立叶变换是具有对称性与周期性，所以可以很好得用这些特性加快运算速度，减少不必要的运算。蝶形运算是其中的一种，而我讲的也就是其中的一种而已，但对于学习FFT应该就够了，如果认为不够的话，那可以自己去找几本书看看。

如果才能将上面的公式与图变成程序呢？也许是我的编程基础太糟糕了，看到这个公式以及实现算法之后，调试了很长一段时间才将程序变得可以运行。在程序实现过程中，最主要的问题是计算机程序与公式不同之处在于程序要考虑计算中的空间存储问题。

 

[新添加]

鉴于有多位网友关注这篇文章，并要求工程源码，但因手上并没有工程源码（不知到丢以哪里去了），所以在这里说明一下工程文件中的基本内容，以使可以利用下面的源码来完成各自手头上的工程或学习。

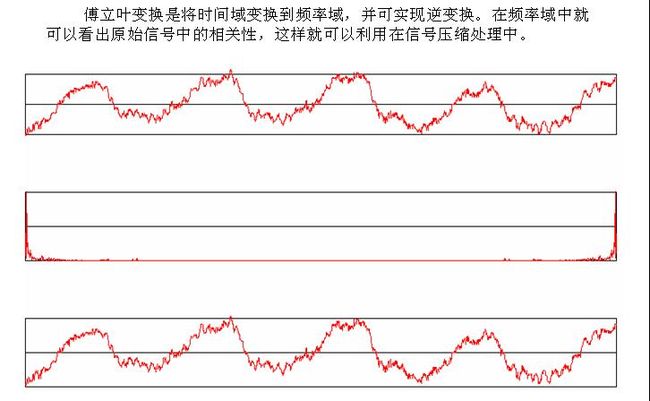
上图就是原始波形的图像，以及经过FFT变换以及反FFT运算之后得到的图像，中图可以看出FFT变换之后，只需要左端的一小部分就可以将整个波形进行描述，并可对过反FFT还原，这样就可以实现数字信号的分析，存储。

 

 

FFT与反FFT的源码：

/*
Parameter:
f:        point a source sequance f(x)
F:        point a target sequance F(x) by FFT procedure
Function:
the procedure through FFT transform f(x) to F(x)
*/
void  CJPEG::FFT( const  complex < double >   * f, complex < double >   * F,  int  N)
{
    
    //将时域复制至频域
    memcpy(F,f,sizeof(complex<double>) * N);

    //需要多少级蝶形运算
    int r = log(N +1) / log(2);

    //进行倒位序运算
    BitReOrder(F,r);

    //计算Wr因子, 加权系数 
    complex<double> *W = new complex<double>[N/2];
    double angle;    
    for(int i = 0; i < N / 2; i++) 
    { 
        angle = - i * PI * 2 / N; 
        W[i] = complex<double> (cos(angle), sin(angle)); 
        //W[i] = complex<double>(0, exp(-i*2*PI/N));
    } 

    //采用蝶形算法进行快速傅立叶变换
    int DFTn;//第DFTn级
    int k;//分级有多少个蝶形运算
    int d;//蝶形运算的偏移
    int p;//index
    
    //complex<double> *X,*X1,*X2;
    //X1 = new complex<double>[N]; 
    //X2 = new complex<double>[N]; 
    complex<double> X1,X2;
    for( DFTn = 0; DFTn < r; DFTn++){//第几级蝶形运算
        for( k= 0; k < (1 << (r - DFTn - 1)); ++k){//当前列所有的蝶形进行运算
            p = 2 * k *  (1 << DFTn);
            for ( d = 0; d < (1 << DFTn); ++d){//相邻蝶形运算
                //p = k * (1 << (k + 1)) + d;
                X1 = F[p+d];
                X2 = F[p+d+(1 << DFTn)];
                F[p+d] = X1 + X2 * W[d*(1<<(r - DFTn - 1))];
                F[p+d+(1 << DFTn)] = X1 - X2 * W[d*(1<<(r - DFTn - 1))];
            }
        }
    }
    //BitReOrder(F,r);
    for(i = 0; i < N; ++i)
        F[i] /= N;
    delete[] W;

    return;
}



void  CJPEG::IFFT( const  complex < double >   * F, complex < double >   * f,  int  N)
{
    int i;
    complex<double>*T = new complex<double>[N];
    memcpy(T,F,sizeof(complex<double>) * N);
    for(i = 0; i < N; ++i){
        //取共轭
        T[i] = complex<double>(T[i].real(), -T[i].imag());        
    }
    CJPEG::FFT(T,f,N);
    for(i = 0; i < N; ++i){//取共轭，并乘以N
        f[i] = complex<double>(f[i].real(), -f[i].imag());    
        f[i] *= complex<double>(N,0) ;
    }
    delete[] T;
}

int  CJPEG::ReadFraqData( const   char   * lpszFileName,  int  N,  double   * pData)
{
    return 0;
}

int  CJPEG::ReadTimeData( const   char   * lpszFileName,  int  N,  double   * pData)
{
    if(pData == NULL) return -1;
    CTextFile ctf(lpszFileName);
    char sLine[64];
    double dData;
    int i = 0;
    while(!ctf.Eof() && i < N){
        ctf.GetLine(sLine, 64);
        dData = atof(sLine);
        pData[i++] = dData;
    }
    return i;
}

/////////////////////////////////////////// 
//  Function name : BitReverse 
//  Description : 二进制倒序操作 
//  Return type : int 
//  Argument : int src 待倒读的数 
//  Argument : int size 二进制位数 
int  CJPEG::BitReverse( int  src,  int  size) 
{ 
    int tmp = src; 
    int des = 0; 
    for (int i=size-1; i>=0; i--) 
    { 
        des = ((tmp & 0x1) << i) | des; 
        tmp = tmp >> 1; 
    } 
    return des; 
}  

/*
Parameter:
sequ:    point a sequance that f(x)
N:        f(x), the x maxinum
Function:
the procedure change the sequance by this:
    // 101 -> 101
    // 110 -> 011
    // 1010 -> 0101
f(5) -> f(5)
f(6) -> f(3)
f(10) -> f(5)
and so on.
*/
void  CJPEG::BitReOrder(complex < double >   * sequ,  int  r)
{
    complex<double> dTemp;
    int x;
    for(int i = 0; i <(1 << r); ++i){
        x = BitReverse(i,r);
        if (x > i){
            dTemp = sequ[i];
            sequ[i] = sequ[x];
            sequ[x] = dTemp;
        }
    }    
}

人有点懒，现在也就写这些了，代码在winxp + vc6.0上调试过，对照代码与前面的图形应该可以理解基础的FFT。如果需要工程文件请EMAIL联系。~_~