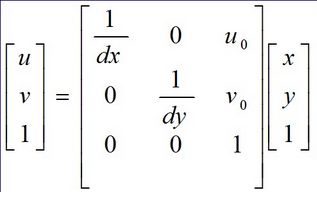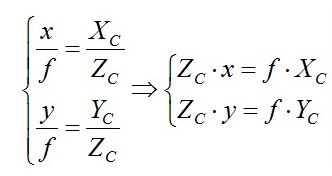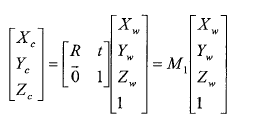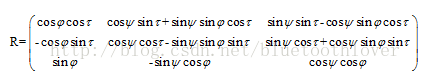相机标定
本文转自:http://blog.csdn.net/jinguangzhi/article/details/10438581
本文转自:http://blog.csdn.net/bluetoothlover/article/details/42707441
一、摄像头定标
摄像头定标一般都需要一个放在摄像头前的特制的标定参照物(棋盘纸),摄像头获取该物体的图像,并由此计算摄像头的内外参数。标定参照物上的每一个特征点相对于世界坐标系的位置在制作时应精确测定,世界坐标系可选为参照物的物体坐标系。在得到这些已知点在图像上的投影位置后,可计算出摄像头的内外参数。
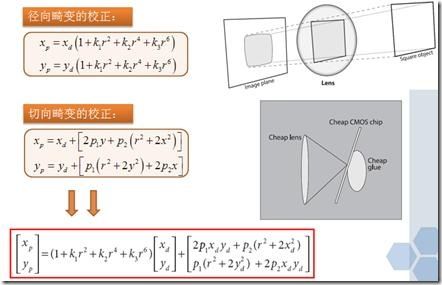
如上图所示,摄像头由于光学透镜的特性使得成像存在着径向畸变,可由三个参数k1,k2,k3确定;由于装配方面的误差,传感器与光学镜头之间并非完全平行,因此成像存在切向畸变,可由两个参数p1,p2确定。单个摄像头的定标主要是计算出摄像头的内参(焦距f和成像原点cx,cy、五个畸变参数(一般只需要计算出k1,k2,p1,p2,对于鱼眼镜头等径向畸变特别大的才需要计算k3))以及外参(标定物的世界坐标)。 OpenCV 中使用的求解焦距和成像原点的算法是基于张正友的方法( pdf ),而求解畸变参数是基于 Brown 的方法( pdf )。
二. 棋盘图像数目应该取多少对摄像头定标比较适宜?
OpenCV中文论坛上piao的帖子《在OpenCV中用cvCalibrateCamera2进行相机标定(附程序) 》中指出影响摄像头定标结果的准确性和稳定性的因素主要有三个:
(1) 标定板所在平面与成像平面(image plane)之间的夹角;
(2) 标定时拍摄的图片数目(棋盘图像数目);
(3) 图像上角点提取的不准确。
感觉OpenCV1.2以后对图像角点的提取准确度是比较高的,cvFindChessboardCorners 和 cvFindCornerSubPix结合可以获得很好的角点检测效果(hqhuang1在《[HQ]角点检测(Corner Detection) cvFindCornerSubPix 使用范例 》中给出了相关的应用范例)。因此,影响定标结果较大的就是标定板与镜头的夹角和棋盘图像数目,在实际定标过程中,我感觉棋盘图像数目应该大于20张,每成功检测一次完整的棋盘角点就要变换一下标定板的姿态(包括角度、距离) 。
1. 相机模型中的四个平面坐标系:
(1)图像像素坐标系(u,v)
以像素为单位,是以图像的左上方为原点的图像坐标系;
(2)图像物理坐标系(也叫像平面坐标系)(x,y)
以毫米为单位,用物理单位表示图像像素位置,定义坐标系OXY,原点O定义在相机与图像平面交点;
(3)相机坐标系(Xc,Yc,Zc)
以毫米为单位,以相机的光心作为原点,Zc轴与光轴重合,并垂直于成像平面,且取摄影方向为正方向,Xc、Yc轴 与图像物理坐标系的x,y轴平行,且OcO为摄像机的焦距f;
(4)世界坐标系(Xw,Yw,Zw)
根据具体情况而定,该坐标系描述环境中任何物体的位置,根据具体情况而定,满足右手法则;
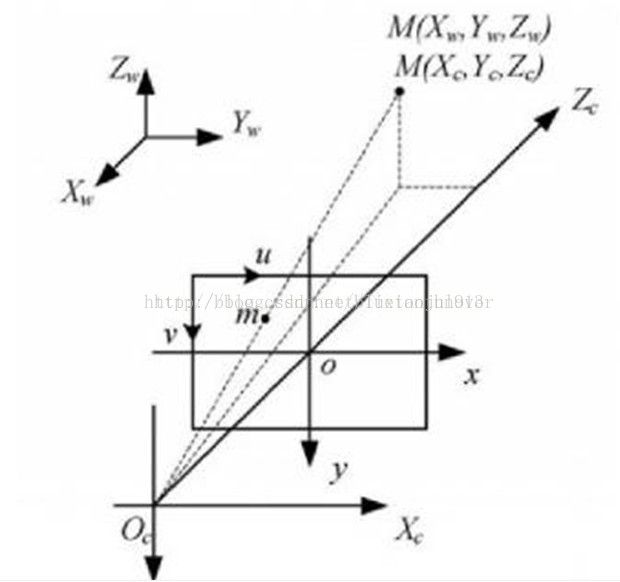
关于这几个坐标系解释很多,但是表示到完整的坐标系上的话都是一个东西,不必纠结,当然我纠结了好久 ········如图:
2.相机的内外参数
标定的主要目的就是求解相机参数。内容如下:
摄像机的内参数:摄像机内参数矩阵(fx,fy,u0,v0)和畸变系数(三个径向k1,k2,k3,两个切向p1,p2)
摄像机的外参数: 旋转向量(大小为1×3的矢量或旋转矩阵3×3)和平移向量(Tx,Ty,Tz)。
3.常用坐标系之间的转换
3.1 像素坐标与像平面坐标系之间的转换
由上述相机坐标模型可以得到如下关系:
(1)
上述公式中我们假设物理坐标系中的单位为毫米,那么dx的的单位为:毫米/像素。那么x/dx的单位就是像素了,即和u的单位一样都是像素,u0 ,v0是图像中心(光轴与图像平面的交点)坐标,dx ,dy分别为一个像素在X 与Y 方向上的物理尺寸.上式表示为齐次坐标与矩阵形式表示出来即为:
(2)
其逆关系可表示为:
(3)