线性代数学习心得（二）矩阵的逆和矩阵变换
本文最希望通过维度变换的角度，来思考矩阵的逆、行列式、以及行变换、列变换。
1、矩阵的逆
1.1、矩阵的逆是什么？
我们依旧把矩阵理解为函数或者说是映射。假设存在矩阵 
向量
。 那么
可以看成是 
。
我们令矩阵F的逆矩阵为 
。也就是函数 。
若 
也就是说，
是 
的输出。显然矩阵*向量 = 向量 。那么也是向量。
。
由此看出，原 矩阵把 向量映射成 向量，而逆矩阵 
就可以把 向量映射成。
写成数学式： 
。
1.2、矩阵不可逆的情况
1.2.1 矩阵的秩
如果你了解些许函数的概念的话，你就能够明白矩阵可逆的条件了。既然矩阵可以映射，还能够通过映射的值找到原来的值。那么矩阵运算过程中就不能有数据丢失，就是函数中的一对一函数。
简单的说：矩阵 可逆的条件是，对于任意两个不相同的向量
必定
。
关于矩阵的秩，大家都知道，矩阵有n行数字不全为0，矩阵的秩就是n。所以矩阵的秩就是矩阵的维度。
我们也知道，矩阵*向量时输出的向量的维度会与矩阵的维度相等。所以说：矩阵的秩，或者说矩阵的维度，就是该矩阵把向量映射后的维度。
假设矩阵的秩为 2，向量的维度是 3。 矩阵*向量后，向量的维度也是2。这里的数据是必然丢失的。可以想象，一个三维的向量被投射到一个二维的平面上，那么你永远不会知道它原来长什么样。例：
假设我遮住原向量，给你矩阵和乘法的结果。你能知道原向量吗？显然是不可能的，如下：
将这个为题变成方程组，也是三个未知数，两个方程。不可能得出唯一解。所以这不是一对一的，也就意味着你永远找不到原来的向量。
最后得出结论：矩阵满秩时（不为0的行数等于列数），矩阵是可逆的。
1.2.2矩阵中向量平行
矩阵中有向量是平行的，就说明，可以通过某种变换让矩阵降维（使某一行全为0，矩阵的秩减少。这种变换就是行变换，行变换不会改变矩阵原有的信息，后面我们会谈到。）此时，矩阵是不可逆的。
不过，除了矩阵的秩减少，我们可以换一个思维模式得到不可逆这个结论。例如:
显然矩阵的两个列向量
与 
平行或者说共线，同时行向量也平行。
如果你有阅读过我的上一篇线性代数博客，你应该还记得，矩阵乘法就是对矩阵中向量的线性组合。
所以：存在某个向量
那么令 
。
向量 是由 向量 和 线性组合而来。同时这两个向量是共线的。所以 也与这两个向量共线。应该说矩阵 
所有的映射都会与这两条向量共线。
向量 
原本是二维向量，现在被映射到了一条直线上（一维），明显数据是丢失的。
再次得出结论：矩阵中有平行的向量时，矩阵不可逆。
1.2.3矩阵映射后出现出现0向量
当
时，矩阵不可逆。
再回到线性组合的思想，在矩阵中的向量组合中，有0向量。这就说明了某个向量与其他全部向量的某种组合共线。这也就意味着，其他所有的向量可以组合出这个被抛弃的向量的所有情况。
这么说的特别的拗口。如图：
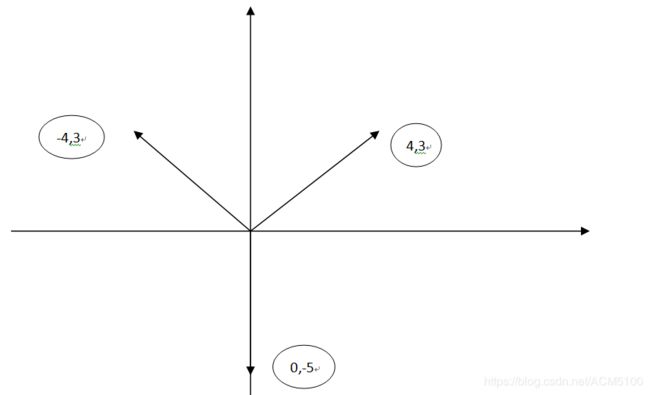
这里有三个向量
令矩阵
，我们利用前面两种向量线性组合，就能获得所有的二维的向量，所以说第三个向量是多余的。
同样，很容易证明这个矩阵不是一对一映射的，这里就不多赘述了。
当我想要组合某一个向量时，我只需要对前面两个向量设置参数就行了。可以说第三个向量与所有的组成方式都没有关系。就是说第三个向量的参数一直设置为0，也不会让某种二维向量映射不出来。也许你听说过这个现象的另一个名字，线性无关。
1.2、逆的求法
1.2.1利用性质
矩阵对于其逆矩阵。就好像函数对于其反函数。
函数具有一个性质，
。函数内嵌套复合函数，其函数值为x。（假设函数
将集合映射到集合
，那么
就是将集合中的元素映射回原来中的元素）。
例如函数 
它的反函数是 
。 
同样 
。
矩阵乘法就是函数嵌套。例如：矩阵 我们理解成 
函数 其逆矩阵
是反函数
。 那么
就相当于
。（这里不得不提，在矩阵乘法时，我们总是从右往左乘，虽然矩阵乘法有交换律但是从右向左乘理解会方便很多。后面讲到矩阵变换时，其作用就会很明显）。
函数与反函数给我们的启发是，它们复合（无论谁在外层）的函数，我们输入 
依旧会得到一个 。映射前后，输入的值没有变化。这一点也同样可以放到矩阵乘法中。也就是说存在向量和矩阵 
。
这也就意味着 
（
矩阵往往作为单位矩阵的标识出现。所谓的单位矩阵，就是它乘某个向量时，向量不会变化）。 同理：
。
我们来举个例子求逆矩阵：
矩阵
（单位矩阵上的左对角线全部为1，其余部分都为0）
这里利用矩阵乘法直接解方程，就能得到各个字母等于多少。从而求出逆矩阵。
1.2.2增广矩阵
我并不太喜欢增广矩阵这个说法，虽然这个名词很重要，但是这里我还是想用原理说清楚为什么可以利用增广矩阵。
我们常常看到的通过增广矩阵的解法是这样的。
求
的逆矩阵 那么画出矩阵 
这个矩阵的左边是原矩阵，右边是单位矩阵。通过行变换，将矩阵变成
这个时候，右边的矩阵
就是原矩阵的逆矩阵。
为什么呢？
这里我们需要理解行变换。行变换就是矩阵乘某些变换矩阵，让行移位或者相消。
例如：对矩阵 变换成
就是行二减二倍行一。前后矩阵蕴含的信息和性质不变。
这个变换过程可以通过矩阵乘法实现，令行二变换的矩阵为
.
。再令行一变换的矩阵为
。
很容易理解 
（记得我前面写的，矩阵从右往左乘。但是在此强调，矩阵乘法是函数嵌套，同理通过乘逆矩阵变回原来的矩阵，就要先乘最后一个被乘的矩阵的逆矩阵。你脱鞋子之后再脱袜子，逆过程就是先穿袜子再穿鞋子）。
既然
而 那么 
。
增广矩阵就是 
左边为 矩阵右边为 矩阵。 
。
所有右边的矩阵就是的逆矩阵。
2.变换矩阵
关于行变换矩阵，我将介绍具体怎么写这个矩阵。已经里面蕴含的思想。
虽然我说了我们常常把矩阵乘法想像为从右往左乘，但是现在你需要反过来，从左往右乘。
这里你得需要前置知识在我的上一篇博客中：https://blog.csdn.net/ACM5100/article/details/88036414
这里重申最为重要的一点：矩阵相乘可以理解成，对左边矩阵的列向量的线性组合，也可以是对右边矩阵行向量的线性组合。
那么我假设你理解这句话：
矩阵
我们令
变换后的矩阵，第一行没有变换（就是第一行的1倍+第二行的0倍）
第二行是由第一行的-2倍加上第二行的1倍 所以 
。
也就是说，变换矩阵不需要计算，可以直接写出来。变换矩阵 记录的是变换前的矩阵 的某一行对变换后的贡献。
当然，这里肯定需要先理解矩阵乘法。再次安利我的上一篇。
3.结语
首先总结一下、我一共介绍了一下几点
1、矩阵逆不存在的情况
2、矩阵的逆的求法
3、变换矩阵的原理
结语没啥好说的。假设你看到这篇博客，欢迎你给出你的宝贵建议。欢迎评论讨论问题。