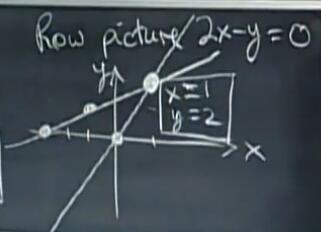线性代数：方程组的几何解释

本节是网易公开课上的麻省理工大学线性代数课程第一节： 方程组的几何解释 的学习笔记。

本节将讨论 线性代数基础 及求 解线性方程组。

从方程组开始讲解，有n个方程和n个未知数，即方程数和未知数个数相等，这种情况最让人舒服。

行图像（row picture）：一个行图像表示一个方程。
列图像（column picture）：

2x2 线性方程组

两方程和两未知数

2x−y=0−x+2y=3

取方程组的每一行作为矩阵的一行，上面方程组的等价于：

[2−1−12][xy]=[03]

最左侧的用矩阵 A 表示（系数矩阵），中间未知数用向量 x （这儿说的向量都是指列向量，除非特殊说明）表示，右侧结果用向量 b 表示，线性方程组可精简为：

Ax=b

2x2 线性方程组的行图像（Row Picture）

在 xy平面 上一次做出方程组中每个方程的图像。先做方程2x - y = 0的图像。

对于该方程，当 y=0 时，x=0，所以改方程的图像经过原点0,0；当x=1时，y=2，所以该方程经过点(1,2)。将两点连线即可得到方程的图像。

对于方程-x + 2y = 3，当y=0时，x=-3；当x=-1时，y=1。连接两点。

两条直线相交于点(1,2)。所以上面方程组的解为x=1, y=2。

2x2 线性方程组的列图像（Column Picture）

取方程组的每一列作为矩阵的一列，上面方程组等价于：

x[2−1]+y[−12]=[03]

该方程组的目的是为了寻找如何将向量 [2, -1] 和 向量 [-1, 2] 进行线性组合，从而得到向量 [0, 3]。即求出 x 和 y 的值。

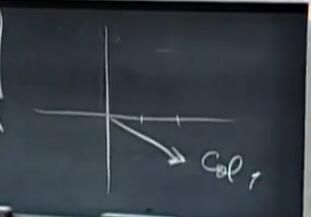
下面开始做出向量 [2,-1]的图像。

然后做出向量 [-1, 2] 的图像。

如何将这两个向量进行线性组合，得到向量 b [0, 3]呢，正确答案是 1 个向量 [2, -1]（列1）， 2 个向量 [-1, 2]（列2）。即：

1[2−1]+2[−12]=[03]

如何画出上面的图像呢？

将 向量 [2, -1] （列1）的终点作为向量 [1, -2] （列2）的起点，然后加上 2 个向量 [1, -2]（列2）。最后终点的向量 b 的坐标 (0, 3)。

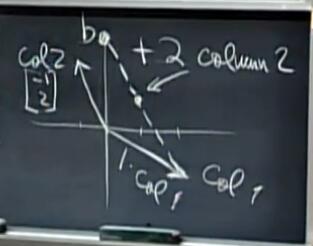
思考一个问题，如果 x 和 y 取所有值，即任意组合的列1和列2的组合，会得到什么结果呢？

答案是任意的一个右侧向量。

3x3 线性方程组

2 x 2 线性方程组比较容易作图求解，3 x 3 线性方程组如何求解呢。通过理解方程组，理解方程组的方式包含上面的 行图像 和 列图像，行图像比较重要，列图像更重要。看下面的方程：

2x−x−y+2y−3y−z+4z=0=−1=4

等价于：

⎡⎣⎢2−10−12−30−14⎤⎦⎥⎡⎣⎢xyz⎤⎦⎥=⎡⎣⎢0−14⎤⎦⎥

3x3 线性方程组的行图像（Row Picture）

在 xyz 坐标系中做出以上三个方程的图像。其中每个方程的图像都是一个平面。最后三个平面会相交于一点。

从上面可以看出，想要做出它的行图像是比较困难的。如果是四维的话，更不好做了。下面使用列图像来完成。

3x3 线性方程组的列图像（Column Picture）

方程组等价于：

x⎡⎣⎢2−10⎤⎦⎥+y⎡⎣⎢−12−3⎤⎦⎥+z⎡⎣⎢0−14⎤⎦⎥=⎡⎣⎢0−14⎤⎦⎥

在坐标系中分别做出这三个向量（列）。

很明显，右侧的向量 b 和系数矩阵 A 列3值是一样的，因此 x=0, y=0, z=1。

思考一个问题，无论右侧向量 b 是多少，是否都能求解方程？等价于代数问题：对任意向量 b，能否求解 Ax=b ？ 用“线性组合”语言来描述：系数矩阵 A 的三个列向量的线性组合，能否覆盖整个三维空间？

对于我们上面用到的系数矩阵 A，答案是肯定的。因为它是一个 “good matrix”，它是 非奇异矩阵，它是 可逆矩阵 。

但是对于有的系数矩阵，答案是否定的。例如，如果系数矩阵的三个列向量在一个平面内（例如，列3等于列1加上列2），那么它们的线性组合也必定在这个平面内。因此，当右侧向量 b 处在这个平面内，则方程有解，否则无解。这种情形称为 奇异，矩阵并非 可逆。

矩阵乘以向量

矩阵 A 乘以向量 x （Ax）得到什么结果呢？

[2153][12]=?

有两种方法可以解决。

一次一列

[2153][12]=1[21]+2[53]=[127]

如何理解呢？Ax（矩阵 A 乘以向量 x） 可以理解矩阵 A 的各列的线性组合。 在这里就是 1 个矩阵 A 的列1 加上 2 个矩阵 A 的列2。

一次一行

[2153][12]=[2∗1+5∗21∗1+3∗2]=[127]