NEFU gcd与lcm 快速幂

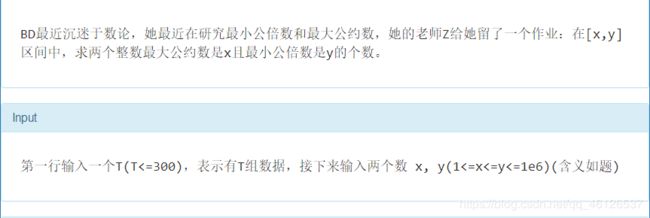
gcd与lcm

gcd（最大公因数）

long long int gcd(long long int a,long long int b)
{
    return b?gcd(b,a%b):a;//相当于 b!=0执行;前 b==0执行：后 //欧几里得算法 递归
}

lcm（最小公倍数）

long long int lcm(long long int a,long long int b)
{
    return (a/gcd(a,b))*b;//揭示了gcd lcm与两数的关系
}

例题：

#include 

using namespace std;

long long int gcd(long long int a,long long int b);

long long int lcm(long long int a,long long int b);

int main()
{
    int n;
    scanf("%d",&n);
    for(int l=0; l<n; l++)
    {
        long long int x,y,res=0,i,j;
        scanf("%lld%lld",&x,&y);
        for(i=x; i<=y; i=i+x)//x必为i的因子，直接加x可简化复杂度
        {
            j=(x*y)/i;//利用gcd lcm与两数的关系简化一重循环
            if(gcd(i,j)==x&&lcm(i,j)==y)
                res++;
        }
        printf("%lld\n",res);
    }
    return 0;
}

long long int gcd(long long int a,long long int b)
{
    return b?gcd(b,a%b):a;
}

long long int lcm(long long int a,long long int b)
{
    return (a/gcd(a,b))*b;
}

#include 

using namespace std;

long long int gcd(long long int a,long long int b);

int main()
{
    int n;
    while(scanf("%d",&n)!=-1)
    {
        for(int m=0;m<n;m++)
        {
            long long int a,b;
            scanf("%lld%lld",&a,&b);
            printf("%lld\n",a*a-2*b*gcd(a,b));//gcd（a，b）==gcd（x，y）可证明 利用互质关系
        }
    }
    return 0;
}

long long int gcd(long long int a,long long int b)
{
    return b?gcd(b,a%b):a;
}

#include 

using namespace std;

long long int gcd(long long int a,long long int b);

int main()
{
    long long int x,y,i;
    scanf("%lld%lld",&x,&y);
    long long int regc,res=0;
    regc=gcd(x,y);//x，y的共有的因子一定是x，y最大公因子的因数
    for(i=1; i*i<regc; i++)//减少时间复杂度  //尽量不要写成i
        if(regc%i==0)
            res=res+2;
    if(i*i==regc)
        res++;
    printf("%lld\n",res);
    return 0;
}

long long int gcd(long long int a,long long int b)
{
    return b?gcd(b,a%b):a;
}

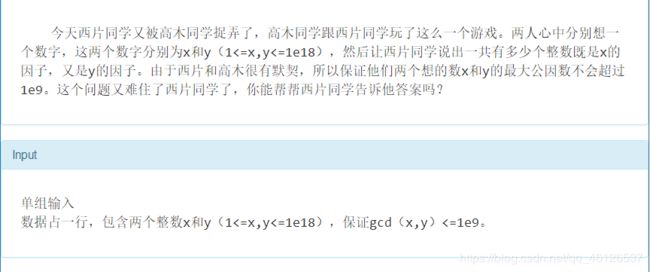
快速幂

核心代码

long long int quickmod(long long int a,long long int b,long long int c)
{
    long long int res=1;
    while(b)
    {
        if(b%2==1)//panduan是否为奇数次幂
            res=res*a%c;//奇数次幂单独乘一个底数，使其变成偶数次幂
        a=a*a%c;
        b/=2;//偶数次幂变平方，缩短时间
    }
    return res;
}

#include 

using namespace std;

long long int quickmod(long long int a,long long int b,long long int c);

int main()
{
    long long int n;
    while(scanf("%lld",&n)!=-1)
    {
        if(n==1）
            printf("6\n");
        else if(n==2)
            printf("18\n");
        else
        {
            long long int res,c=1000000007;
            res=quickmod(3,n-2,c)*18%c;//由题目证明数列从第三项往后是等比数列
            printf("%lld\n",res);
        }
    }
    return 0;
}

long long int quickmod(long long int a,long long int b,long long int c)
{
    long long int res=1;
    while(b)
    {
        if(b%2==1)
            res=res*a%c;
        a=a*a%c;
        b/=2;
    }
    return res;
}

由演算易知：将问题转化为二进制，仅用一位来分析问题，n=0时x只能等于0，n=0时x能等于0或1.因此该数转化为二进制后由几位1，方程就有2的几次方个解。

#include 

using namespace std;

int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        int num=n,i,res=0;
        for(i=0; num!=0; i++)
            num=num/2;//数位右移，判断该数的二进制有几位，直到该数变为0
        for(int j=0; j<i; j++)
            if(n&(1<<j))//二进制枚举左移，判断数位上的是否为1
                res++;
        res=pow(2,res);//此处可以使用快速幂降低时间复杂度 林大oj用pow函数可通过
        printf("%d\n",res);
    }
    return 0;
}