矩阵论
线性空间
- 1、线性空间的定义以及性质
- 1.1、集合与映射(预备知识)
- 1.2、线性空间的定义
- 1.3、定理:线性空间有如下性质:
- 1.4、线性相关性
- 1.5 线性空间的维数
- 2、线性空间的基与坐标
- 2.1、基的定义
- 2.2、坐标的定义
- 3、基变换与坐标变换
1、线性空间的定义以及性质
1.1、集合与映射(预备知识)
集合: 笼统的说是指一些事物(或者对象)组成的整体。
数集: 由数(有限个,无限个)组成的集合。
解集合: 一个线性方程组解的全体组成的集合。
点集合: 一个已知半径和圆心的开圆内的所有点组成的一个集合。
集合的运算: 并( ∪ \cup ∪),交( ∩ \cap ∩)
此外,集合的“和”(+):并不是严格意义上集合的运算,因为它限定了集合中元素须有可加性。
规定空集合是任意集合的子集合(空集合在集合中所起到的作用类似于数0在数的运算中所起到的作用),每个集合都是自身的子集合。
**数域:**一种数集,对四则运算封闭(除数不为0).比如有理数域、实数域(R)和复数域(C)。实数域和复数域是工程上较常用的两个数域。
1.2、线性空间的定义
设V是一个非空集合,其元素用x,y,z等表示;K是一个数域,其元素用k,l,m等表示。如果V满足一下8条性质(分成两类):
Ⅰ 在V中定义一个“加法运算”,即当x,y∈V时,有唯一的和x+y∈V(封闭性),且加法运算满足下列性质:
(1)结合律:x+(y+z)=(x+y)+z;
(2)交换律:x+y=y+xx;
(3)零元律:存在零元素O(不是数0),使x+O=x;
(4)负元律:对于任一元素x∈V,存在唯一元素y∈V,使得x+y=O,且称y为x的负元素,极左(-x),则有x+(-x)=O;
Ⅱ 在V中定义一个“数乘”运算,即当x∈V,k∈K时,有唯一的kx∈V(封闭性),切数乘运算满足下列性质:
(5)数因子分配律:k(x+y)=kx+ky;
(6)分配律:(k+l)x=kx+lk;
(7)结合律:k(lx)=(kl)x;
(8)恒等律:1x=x;(数域中一定有1)
则称V为数域K上的线性空间。
注:
1)线性空间是基于一定数域的。同一个集合,对于不同数域,就可能构成不同的线性空间,甚至对有的数域都能构成线性空间,而对其他的数域不能构成线性空间。
2)两种运算,八条性质。数域K中的运算是具体的四则运算,而V中所定义的加法运算和数乘运算则是抽象的、形式的。
3)除了两种运算和八条性质外,还应注意唯一性、封闭性是否满足。
当数域K为实数域时,V就称为实线性空间;K为复数域时,V就称为复线性空间。
例1、 设 R + R^+ R+={全体实数},其“加法”及“数乘”运算定义为:
x ⊕ y = x y , k ∘ x = x k x \oplus y = xy,k \circ x = {x^k} x⊕y=xy,k∘x=xk证明: R + R^+ R+是实数R上的线性空间。
证:首先要证明两种运算的唯一性和封闭性。
①唯一性和封闭性:
唯一性显然
若x>0,y>0,k∈R,则有 x ⊕ y = x y ∈ R + , k ∘ x = x k ∈ R + x \oplus y = xy\in R^+,k \circ x = {x^k}\in R^+ x⊕y=xy∈R+,k∘x=xk∈R+封闭性得证。
②八条性质:
1)结合律: x ⊕ ( y ⊕ z ) = x ( y z ) = ( x y ) z = ( x ⊕ y ) ⊕ z x\oplus(y\oplus z)=x(yz)=(xy)z=(x\oplus y)\oplus z x⊕(y⊕z)=x(yz)=(xy)z=(x⊕y)⊕z
2)交换律: x ⊕ y = x y = y x = y ⊕ x x\oplus y=xy=yx=y\oplus x x⊕y=xy=yx=y⊕x
3)零元律:1是零元素,$x\oplus 1=x\cdot 1=x$, [ x ⊕ O = x → x O = x → O = 1 ] [x\oplus O=x\to xO=x\to O=1] [x⊕O=x→xO=x→O=1]
4)负元律: 1 x \frac{1}{x} x1是x的负元素 x ⊕ 1 x = x ⋅ 1 x = 1 x\oplus\frac{1}{x}=x\cdot\frac{1}{x}=1 x⊕x1=x⋅x1=1, [ x ⊕ y = O ] [x\oplus y=O] [x⊕y=O]
5)数因子分配率: k ∘ ( x ⊕ y ) = ( x y ) k = x k y k = ( k ∘ x ) ⊕ ( k ∘ y ) k\circ(x\oplus y)=(xy)^k=x^ky^k=(k\circ x)\oplus(k\circ y) k∘(x⊕y)=(xy)k=xkyk=(k∘x)⊕(k∘y)
6)分配律: ( k + l ) ∘ x = x k + l = x k x l = ( k ∘ x ) ⊕ ( l ∘ x ) (k+l)\circ x=x^{k+l}=x^kx^l=(k\circ x)\oplus(l\circ x) (k+l)∘x=xk+l=xkxl=(k∘x)⊕(l∘x)
7)结合律: k ∘ ( l ∘ x ) = ( x l ) k = x k l = ( k l ) ∘ x k\circ(l\circ x)=(x^l)^k=x^{kl}=(kl)\circ x k∘(l∘x)=(xl)k=xkl=(kl)∘x
8)恒等律: 1 ∘ x = x 1 = x 1\circ x=x^1=x 1∘x=x1=x
八条性质都成立,所以 R + R^+ R+是实数域R上的线性空间。
1.3、定理:线性空间有如下性质:
(1)零元素是唯一的,任一元素的负元素也是唯一的。
(2)如下恒等式成立:0x=O,(-1)x=(-x)。
证明:(1)采用反证法:
①零元素是唯一的。设存在两个零元素 O 1 O_1 O1和 Q 2 Q_2 Q2,则由于 O 1 O_1 O1和 Q 2 Q_2 Q2都是零元素,按零元律和交换率有:
O 1 + O 2 = O 1 = O 2 = O 2 + O 1 O_1+O_2=O_1=O_2=O_2+O_1 O1+O2=O1=O2=O2+O1
所以 O 1 = O 2 O_1=O_2 O1=O2,即 O 1 和 O 2 O_1和O_2 O1和O2相同,与假设相矛盾,故只有一个零元素。
②任一元素的负元素也是唯一的。假设 ∀ x ∈ V \forall x \in V ∀x∈V,存在两个负元素y和z,则更具负元律有: x + y = O = x + z x+y=O=x+z x+y=O=x+z
y = y + O = y + ( x + z ) = ( y + x ) + z = O + z = z y=y+O=y+(x+z)=(y+x)+z=O+z=z y=y+O=y+(x+z)=(y+x)+z=O+z=z
即y与z相同,故负元素唯一。
(2)
①设w=0x,则x+w=1x+0x=(1+0)x=x,故w=O
②设w=(-1)x,则x+w=1x+(-1)x=0x=O,故w=-x。
1.4、线性相关性
线性空间中相关性概念与线性代数中向量组线性相关性概念类似。
线性组合: ∀ x 1 , x 2 , x 3 , . . . , x m ∈ V , c 1 , c 2 , c 3 , . . . c m ∈ K \forall x_1,x_2,x_3,...,x_m\in V,c_1,c_2,c_3,...c_m\in K ∀x1,x2,x3,...,xm∈V,c1,c2,c3,...cm∈K,使得 c 1 x 1 + c 2 x 2 + . . . + c m x m = ∑ i = 1 m c i x i c_1x_1+c_2x_2+...+c_mx_m=\sum\limits_{i=1}^mc_ix_i c1x1+c2x2+...+cmxm=i=1∑mcixi称为元素组的一个线性组合。
线性表示: V中某个元素x可以表示为其中某个元素的线性组合,则称x可由该元素组线性表示。
线性相关性: 如果存在一组不全为0的数 c 1 , c 2 , c 3 , . . . c m ∈ K c_1,c_2,c_3,...c_m\in K c1,c2,c3,...cm∈K,使得对于元素 x 1 , x 2 , x 3 , . . . , x m ∈ V x_1,x_2,x_3,...,x_m\in V x1,x2,x3,...,xm∈V有 ∑ i = 1 m c i x i = 0 \sum\limits_{i=1}^mc_ix_i=0 i=1∑mcixi=0则称元素组 x 1 , x 2 , x 3 , . . . , x m x_1,x_2,x_3,...,x_m x1,x2,x3,...,xm线性相关,否则称其线性无关
1.5 线性空间的维数
定义: 线性空间V中最大线性无关元素组所含元素的个数称为V的维数,记作 d i m V dim V dimV
例:全体m×n阶实矩阵的集合构成一个实线性空间(对于矩阵加法和数对矩阵的乘法运算,),求其维数。
解:一个直接的方法就是找一个最大线性无关组,其元素尽可能的简单
令 E i j E_{ij} Eij为这样的一个m×x阶矩阵,其(i,j)元素为1,其余元素为零。
显然这样的矩阵共有m×n个,构成一个具有m×n个元素的线性无关元素组 { E 11 , E 12 , . . . , E 1 n , E 21 , E 22 , . . . , E 2 n ; . . . ; E m 1 , E m 2 , . . . , E m n } \{E_{11},E_{12},...,E_{1n},E_{21},E_{22},...,E_{2n};...;E_{m1},E_{m2},...,E_{mn}\} {E11,E12,...,E1n,E21,E22,...,E2n;...;Em1,Em2,...,Emn}> 另一方面,还需要说明元素个数最大。对于任意的 A = ( a i j ) A=(a_{ij}) A=(aij)都可以由以上元素组线性表示。 A = ∑ i , j a i j E i j → ∑ i , j a i j E i j − A = 0 A=\sum\limits_{i,j}a_{ij}E_{ij}\to \sum\limits_{i,j}a_{ij}E_{ij}-A=0 A=i,j∑aijEij→i,j∑aijEij−A=0即 { E i j ∣ i = 1 , 2... , m ; j = 1 , 2... , n } \{E_{ij}|i=1,2...,m;j=1,2...,n\} {Eij∣i=1,2...,m;j=1,2...,n}构成了最大线性无关元素组,所以该空间的维数为m×n。
2、线性空间的基与坐标
2.1、基的定义
设V是数域K上的线性空间, x 1 , x 2 , x 3 , . . . x r ( r ≥ 1 ) x_1,x_2,x_3,...x_r(r≥1) x1,x2,x3,...xr(r≥1)是属于V的r个任意元素,如果它满足:
(1) x 1 , x 2 , x 3 , . . . x r ( r ≥ 1 ) x_1,x_2,x_3,...x_r(r≥1) x1,x2,x3,...xr(r≥1)线性无关;
(2)V中任一向量x均可以由 x 1 , x 2 , x 3 , . . . x r x_1,x_2,x_3,...x_r x1,x2,x3,...xr线性表示。
则称 x 1 , x 2 , x 3 , . . . x r ( r ≥ 1 ) x_1,x_2,x_3,...x_r(r≥1) x1,x2,x3,...xr(r≥1)为V的一个基,并称 x 1 , x 2 , x 3 , . . . x r x_1,x_2,x_3,...x_r x1,x2,x3,...xr为该基的基元素。
注:1)基正是V中最大线性无关元素组;V的维数正是基中所含元素的个数。2)基是不唯一的,但不同的基所含元素个数相等。
例:考虑全体复数所形成的集合C,如果K=C(复数域),则该集合对复数假发和复数乘法构成线性空间,其基可取为1,空间维数为1;如果取K=R(实数域),则该集合对复数加法以及实数对复数的数乘构成线性空间,其基可以取{1,i},空间维数为2.
| 数域K | 两种运算 | 基 | 一般元素 | 空间类型 | 维数 |
|---|---|---|---|---|---|
| 复数域C | (1)复数加法;(2)复数对复数的数乘 | {1} | c = c ⋅ 1 c=c\cdot 1 c=c⋅1 | 复线性空间 | 1 |
| 实数域R | (1)复数加法;(2)实数对复数的数乘 | {1,i} | c = a ⋅ 1 + b ⋅ 1 c=a\cdot 1+b\cdot 1 c=a⋅1+b⋅1 | 实线性空间 | 2 |
2.2、坐标的定义
线性空间 V n V^n Vn的一个基 x 1 . x 2 , . . . x n x_1.x_2,...x_n x1.x2,...xn为 V n V_n Vn的一个坐标系, ∀ x ∈ V n \forall x\in V^n ∀x∈Vn,它在基下的线性表示为: ∑ i = 1 n ξ i x i ( ξ i ∈ K , x i ∈ V n , i = 1 , 2 , . . . , n ) \sum\limits_{i=1}^n\xi_ix_i\quad(\xi_i\in K,x_i\in V^n,i=1,2,...,n) i=1∑nξixi(ξi∈K,xi∈Vn,i=1,2,...,n)
讨论:(1)一般来说,线性空间以及其元素是抽象的对象,不同空间的元素完全可以具有千差万别的类别以及性质。但坐标表示却把它们统一了起来,坐标表示把这种差别留给了基和基元素,由坐标所组成的新向量仅由数域中的数表示出来;(2)更进一步,原本抽象的假“加法”以及“数乘”经过坐标表示就演化为向量加法以及数对向量的数乘;(3)同一元素在不同坐标系中的坐标是不同的。
(1) x + y = ( ξ 1 x 1 + ξ 2 x 2 + . . . + ξ n x n ) + ( η 1 x 1 + η 2 x 2 + . . . + η n x n ) = ( ξ 1 + η 1 ) x 1 + ( ξ 2 + η 2 ) x 2 + . . . + ( ξ n + η n ) x n \begin{array}{ccccc} x + y& = & ({\xi _1}{x_1} + {\xi _2}{x_2} + ... + {\xi _n}{x_n}) + ({\eta _1}{x_1} + {\eta _2}{x_2} + ... + {\eta _n}{x_n})\\ & = & ({\xi _1} + {\eta _1}){x_1} + ({\xi _2} + {\eta _2}){x_2} + ... + ({\xi _n} + {\eta _n}){x_n} \end{array} x+y==(ξ1x1+ξ2x2+...+ξnxn)+(η1x1+η2x2+...+ηnxn)(ξ1+η1)x1+(ξ2+η2)x2+...+(ξn+ηn)xn正对应:
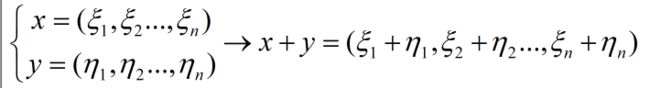
(2) k x = k ( ξ 1 x 1 , ξ 2 x 2 . . . , ξ n x n ) = ( k ξ 1 ) x 1 + ( k ξ 2 ) x 2 + . . . + ( k ξ n ) x n kx = k({\xi _1}{x_1},{\xi _2}{x_2}...,{\xi _n}{x_n}) = (k{\xi _1}){x_1} + (k{\xi _2}){x_2} + ... + (k{\xi _n}){x_n} kx=k(ξ1x1,ξ2x2...,ξnxn)=(kξ1)x1+(kξ2)x2+...+(kξn)xn → ( k ξ 1 , k ξ 2 , . . . , k ξ n ) \to(k\xi_1,k\xi_2,...,k\xi_n) →(kξ1,kξ2,...,kξn)
正对应: x = ( ξ 1 , ξ 2 . . . , ξ n ) → k x = ( k ξ 1 , k ξ 2 , . . . , k ξ n ) {x = ({\xi _1},{\xi _2}...,{\xi _n})}\to kx=(k\xi_1,k\xi_2,...,k\xi_n) x=(ξ1,ξ2...,ξn)→kx=(kξ1,kξ2,...,kξn)
