使用Qiskit学习量子计算_4数学基础（上）

本节主要内容

• 概述
• 向量和向量空间
• 矩阵和矩阵运算
• 线性相关和基

概述

线性代数是量子计算的描述语言。因此，对线性代数所基于的基本数学概念有一个很好的理解，有助于得出量子计算中看到的许多令人惊奇和有趣的结构。本部分的目的是建立入门级线性代数知识的基础。

向量和向量空间

首先，将讨论量子计算中最重要的数学概念之一：矢量。

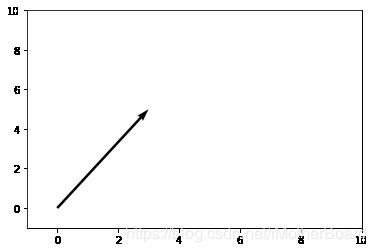
通常，向量 $|\text{v}⟩$ 被定义为向量空间集合中的元素。一个更直观的定义是向量“是具有方向和幅度的数学量”。例如，考虑向量$\left(\begin{array}{c}\text{3}\\ \text{5}\end{array}\right)$ ，作图显示如下：

from matplotlib import pyplot as plt
import numpy as np
from qiskit import *
from qiskit.visualization import plot_bloch_vector

plt.figure()
ax = plt.gca()
ax.quiver([3], [5], angles='xy', scale_units='xy', scale=1)
ax.set_xlim([-1, 10])
ax.set_ylim([-1, 10])
plt.draw()
plt.show()

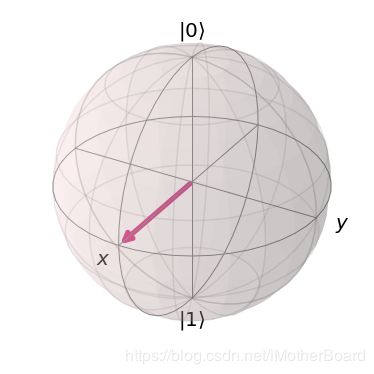
在量子计算中，经常处理状态向量，可以使用Bloch球将其可视化。例如，代表量子系统状态的向量可能看起来像如下所示的箭头，被包围在Bloch球内部。所谓Bloch球的即“状态空间”，是状态向量可以“指向”的所有可能点：

plot_bloch_vector([1, 0, 0])

上图中表示的状态是$|0⟩$ 和 $|1⟩$ 的叠加态。bloch球上的状态允许旋转到球表面的任何位置，不同的位置代表不同的状态。

现在来看向量的正式定义，即向量是向量空间的元素。一个向量空间 $V$ 是域$F$上一组向量的集合，且需要满足两个条件成立。

• 两个向量的向量加仍在该集合中，即$|a⟩,|b⟩\in V$ ，$|a⟩+|b⟩=|c⟩$仍在$V$。
• 标量乘法，对$|a⟩\in V$ 和某个 $n\in F$，其乘积 $n|a⟩$仍在$V$.

现在，我们将通过一个简单示例来阐明上述的定义。让我们证明在域 $\mathbb{R}$上的集合${\mathbb{R}}^2$是一个向量空间。首先，

$$\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)+\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=\left(\begin{array}{c}{x}_1+x_2\\ y_1+y_2\end{array}\right)$$

因为两个实数之和仍为实数，所上述式子的运算结果仍然在${\mathbb{R}}^2$中。同时

$$n|v⟩=\left(\begin{array}{c}nx\\ ny\end{array}\right)\in V\forall n\in \mathbb{R}$$

因为两个实数之和积仍为实数，所上述式子的运算结果也在${\mathbb{R}}^2$中。因此，在域$\mathbb{R}$上的集合${\mathbb{R}}^2$是一个向量空间。

矩阵和矩阵运算

现在来看另一个重要的概念矩阵。

一个简单的矩阵示例如下：

$$M=\left(\begin{array}{ccc}1& -2& 3\\ 1& 5i& 0\\ 1+i& 7& -4\end{array}\right)$$

矩阵运算中，矩阵的乘法非常重要，也很简单，不会的话自己百度。这里给一个示例，

$$\left(\begin{array}{cc}2& 0\\ 5& -1\end{array}\right)\left(\begin{array}{cc}-3& 1\\ 2& 1\end{array}\right)=\left(\begin{array}{cc}(2)(-3)+(0)(2)& (2)(1)+(0)(1)\\ (5)(-3)+(-1)(2)& (5)(1)+(-1)(1)\end{array}\right)=\left(\begin{array}{cc}-6& 2\\ -17& 4\end{array}\right)$$

在量子计算中，矩阵用来干什么？答案是用来对状态向量进行变换，如下所示：

$$|v⟩\to |v^{\prime }⟩=M|v⟩$$

这个变换的运算规则就是上面提到的矩阵乘法，因为向量可以看作是只有一列的矩阵。实际上，量子计算就是在量子计算机中通过应用量子门序列操纵量子位。每个量子门可以表示为可作用于状态向量的矩阵。例如，常见的量子门是Pauli-X门，它由以下矩阵表示：

$${\sigma }_x=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$$

此门的作用类似于经典的NOT逻辑门。它将基本状态$|0⟩$映射到$|1⟩$，将$|1⟩$映射到$|0⟩$（“翻转”状态）。将两个基本状态写为列向量：

$$|0⟩=\left(\begin{array}{c}1\\ 0\end{array}\right)|1⟩=\left(\begin{array}{c}0\\ 1\end{array}\right)$$

当我们Pauli-X应用于上述每个基本向量时：

$${\sigma }_x|0⟩=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}(0)(1)+(1)(0)\\ (1)(1)+(0)(0)\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)=|1⟩$$

$${\sigma }_x|1⟩=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}0\\ 1\end{array}\right)=\left(\begin{array}{c}(0)(0)+(1)(1)\\ (1)(0)+(0)(1)\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right)=|0⟩$$

在量子计算中，我们经常会遇到两种重要的矩阵类型：厄米矩阵和幺正矩阵。前者在量子力学的研究中更为重要，但在量子计算的研究中仍然有必要进行讨论。后者在量子力学和量子计算中都具有无与伦比的重要性。

厄米矩阵是一个与其共轭转置相等的矩阵（用$†$符号表示）。这意味着翻转Hermitian矩阵的虚部符号，然后沿其主对角线作转置，将生成相等的矩阵。例如，量子计算中常用的Pauli-Y矩阵是Hermitian：

$${\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)\Rightarrow {\sigma }_y^{†}=\left(\begin{array}{cc}0& -(i)\\ -(-i)& 0\end{array}\right)=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)={\sigma }_y$$

幺正矩阵是逆矩阵等于其自身共轭转置的矩阵。矩阵$A$的逆矩阵记为$A^{-1}$：

$$A^{-1}A=A{A}^{-1}=\mathbb{I}$$

其中$ \mathbb {I} $是单位矩阵。单位矩阵沿主对角线（从左上到右下）全为$1$ ，在所有其他位置为$0$ 。之所以称为单位矩阵，是因为它乘以任何其他矩阵仍为该矩阵本身。

当矩阵的大小大于$2\times 2$时，逆矩阵的计算比较复杂。对于$2\times 2$矩阵，其逆矩阵为：

$$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\Rightarrow A^{-1}=\frac{1}{\text{det}A}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right),$$

其中$\text{det}A$是矩阵的行列式。在$2\times 2$的情况下，$\text{det}A=ad-bc$。

在量子计算中，由于我们遇到的大多数矩阵都是幺正矩阵，因此我们可以通过采用共轭转置来简单给出逆矩阵。

让我们看一个基本的例子。Pauli-Y矩阵除了是厄米矩阵外，也是幺正矩阵（它等于其共轭转置，也等于其逆矩阵；因此，Pauli-Y矩阵是其自身的逆矩阵！）。我们可以验证此矩阵实际上是幺正的：

$${\sigma }_y=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right){\sigma }_y^{†}=\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right)\Rightarrow {\sigma }_y^{†}{\sigma }_y=\left(\begin{array}{cc}(0)(0)+(-i)(i)& (0)(-i)+(-i)(0)\\ (i)(0)+(0)(i)& (i)(-i)+(0)(0)\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)=\mathbb{I}$$

线性相关和基

考虑某个向量空间 $V$。我们说某个空间$V_S$ 是$V$的线性子空间，是指当$V_S$为向量空间$V$的一个非空子集，$V_S$中向量的线性组合仍在$V_S$中，且零向量$0\in V_S$。

某个向量 $|v_1⟩,...,|v_n⟩$ 在域$F$上的线性组合定义如下，其中$f_i$ 是域 $F$中的元素

$$|v⟩=f_1|v_1⟩+f_2|v_2⟩+...+f_n|v_n⟩=\sum _i{f}_i|v_i⟩$$

某个向量集合$|v_1⟩,...,|v_n⟩$是线性相关的，是指存在一组系数 $b_i\in F$ 使得下式成立,这组系数中至少有一个非$0$元素，不妨设为$b_a$

$$b_1|v_1⟩+b_2|v_2⟩+...+b_n|v_n⟩=\sum _i{b}_i|v_i⟩=0,$$

上式等价于该向量集合$|v_1⟩,...,|v_n⟩$中的某个元素 $|v_a⟩$可以被表示为其他元素的线性组合

$$\sum _i{b}_i|v_i⟩=b_a|v_a⟩+\sum _{i,i\ne a}{b}_i|v_i⟩=0\Rightarrow |v_a⟩=-\sum _{i,i\ne a}\frac{b_i}{b_a}|v_i⟩=\sum _{i,i\ne a}{c}_i|v_i⟩$$

现在来看一个具体示例，考虑在 ${\mathbb{R}}^2$上的两个二维向量， $|a⟩=\left(\begin{array}{c}1\\ 0\end{array}\right)$ 和$|b⟩=\left(\begin{array}{c}2\\ 0\end{array}\right)$。在域 $\mathbb{R}$上，这两个向量是线性相关的，如下：

$$2|a⟩-|b⟩=0$$

相应的，某个向量集合$|v_1⟩,...,|v_n⟩$是线性无关的，是指不存在一组含有非零元的系数 $b_i\in F$ 使得下式成立

$$b_1|v_1⟩+b_2|v_2⟩+...+b_n|v_n⟩=\sum _i{b}_i|v_i⟩=0,$$

线性空间的一组基是指张成该向量空间的最小线性无关组，这组基中的元素个数称为该线性空间的维数。这里的张成可以简单理解为该向量空间中的向量都可以被这组基线性表出。

基之所以很重要，因为它们允许我们“缩小”向量空间并仅用几个向量表示它们。通常可以将关于基的某些结论推广到整个向量空间。

在量子计算中，我们经常遇到的一组基是$|0⟩,|1⟩$ 。我们可以将任何其他量子位状态写为这两个基向量的线性组合。例如，线性组合

$$\frac{|0⟩+|1⟩}{\sqrt{2}}$$

这个线性组合就是量子计算中常提到的量子态叠加，在这里实际就是指代表之间的叠加 $|0⟩$ 和$|1⟩$ 基态的等概率叠加。

更多精彩，请