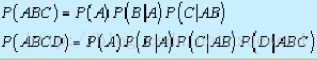概率论(二)- 随机事件与随机事件的概率
随机事件
引例一,掷两次硬币,其可能结果有:{上上;上下;下上;下下}
则出现两次面向相同的事件A与两次面向不同的事件B都是可能出现,也可能不出现的。引例二,掷一次骰子,其可能结果的点数有:{1,2,3,4,5,6}
则出现偶数点的事件A,点数≤4的事件B都是可能出现,也可能不出现的事件。
从引例一与引例二可见,有些事件在一次试验中,有可能出现,也可能不出现,即它没有确定性结果,这样的事件,我们叫随机事件。
(一)随机事件:
在一次试验中,有可能出现,也可能不出现的事件,叫随机事件,习惯用A、B、C表示随机事件。
由于本课程只讨论随机事件,因此今后我们将随机事件简称事件。
虽然我们不研究在一次试验中,一定会出现的事件或者一定不出现的事件,但是有时在演示过程中要利用它,所以我们也介绍这两种事件。
必然事件:在一次试验中,一定出现的事件,叫必然事件,习惯用Ω表示必然事件。
例如,掷一次骰子,点数≤6的事件一定出现,它是必然事件。
不可能事件:在一次试验中,一定不出现的事件叫不可能事件,而习惯用φ表示不可能事件。
例如,掷一次骰子,点数>6的事件一定不出现,它是不可能事件。
(二)基本(随机)事件
随机试验的每一个可能出现的结果,叫基本随机事件,简称基本事件,也叫样本点,习惯用ω表示基本事件。 例如,掷一次骰子,点数1,2,3,4,5,6分别是基本事件,或叫样本点。 全部基本事件叫基本事件组或叫样本空间,记作Ω,当然Ω是必然事件。
(三)随机事件的关系
(1)事件的包含:
若事件A发生则必然导致事件B发生,就说事件B包含事件A,记作
。
例如,掷一次骰子,A表示掷出的点数≤2,B表示掷出的点数≤3。∴A={1,2},B={1,2,3}, 所以A发生则必然导致B发生。显然有
(2)事件的相等:
若
且
,就记A=B,即A与B相等,事件A等于事件B,表示A与B实际上是同一事件
(四)事件的运算
(1)和事件:
事件A与事件B中至少有一个发生的事件叫事件A与事件B的和事件,记作AUB:或A+B
例如,掷一次骰子,A={1,3,5};B={1,2,3} 则和事件A+B={1,2,3,5}
显然有性质:
1.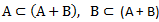
2. 若,则有A+B=B
3. A + A = A。
(2)积事件:
事件A与事件B都发生的事件叫事件A与事件B的积事件,记作:AB或A∩B
例如,掷一次骰子,A={1,3,5};B={1,2,3},则AB={1,3} 显然有性质:
;
- 若
,则有AB=A;
- AA = A.
(3)差事件:
事件A发生而且事件B不发生的事件叫事件A与事件B的差事件,记作(A-B)
例如,掷一次骰子,A={1,3,5};B={1,2,3},则A-B={5}
显然有性质:
1.;
2. 若,则有A-B=Φ;
3. A-B=A-AB
(4)互不相容事件:
若事件A与事件B不能都发生,就说事件A与事件B互不相容(或互斥)即AB=Φ
例如,掷一次骰子,A={1,3,5};B={2,4} ∴AB=Φ
(5)对立事件:
事件A不发生的事件叫事件A的对立事件。记作
。
例如,掷一次骰子,A={1,3,5},则;
显然,对立事件有性质:
1.;
2.;
3.
注意:A与B对立,则A与B互不相容,反之不一定成立。
例如在考试中A表示考试成绩为优,B表示考试不及格。A与B互不相容,但不对立。
下面图1.1至图1.6用图形直观的表示事件的关系和运算,其中正方形表示必然事件或样本空间Ω



例1
A,B,C表示三事件,用A,B,C的运算表示以下事件。
(1)A,B,C三事件中,仅事件A发生
(2)A,B,C三事件都发生
(3)A,B,C三事件都不发生
(4)A,B,C三事件不全发生
(5)A,B,C三事件只有一个发生
(6)A,B,C三事件中至少有一个发生
例2
某射手射击目标三次:A1表示第1次射中,A2表示第2次射中,A3表示第3次射中。B0表示三次中射中0次,B1表示三次中射中1次,B2表示三次中射中2次,B3表示三次中射中3次,请用A1、A2、A3的运算来表示B0、B1、B2、B3
例3
A,B,C表示三事件,用A,B,C的运算表示下列事件。
(1)A,B都发生且C不发生
(2)A与B至少有一个发生而且C不发生
(3)A,B,C都发生或A,B,C都不发生
(4)A,B,C中最多有一个发生
(5)A,B,C中恰有两个发生
(6)A,B,C中至少有两个发生
随机事件的概率
(一)频率
(1)在相同条件下,进行了n次试验,在这n次试验中,事件A发生了nA次,则事件A发生的次数nA叫事件A发生的频数。
(2)比值nA/n称为事件A发生的频率,记作fn(A)。
历史上有不少人做过抛硬币试验,其结果见下表,用A表示出现正面的事件:

从上表可见,当试验次数n大量增加时,事件A发生的频率fn(A)会稳定某一常数,我们称这一常数为频率的稳定值。例如从上表可见抛硬币试验,正面出现的事件A的频率fn(A)的稳定值大约是0.5。
(二)概率
事件A出现的频率的稳定值叫事件A发生的概率,记作P(A)
实际上,用上述定义去求事件A发生的概率是很困难的,因为求A发生的频率fn(A)的稳定值要做大量试验,它的优点是经过多次的试验后,给人们提供猜想事件A发生的概率的近似值。
粗略地说,我们可以认为事件A发生的概率P(A)就是事件A发生的可能性的大小,这种说法不准确,但人们容易理解和接受,便于应用。
下面我们不加证明地介绍事件A的概率P(A)有下列性质:
(1)0≤P(A)≤1 ;
(2)P(Ω)=1,P(Φ)=0 ;
(3)若A与B互斥,即AB=Φ,则有P(A+B)=P(A)+P(B) 。
若A1,A2,……,An互斥,则有:
![]()
(三)古典概率模型
若我们所进行的随机试验有下面两个特点:
(1)试验只有有限个不同的结果;
(2)每一个结果出现的可能性相等,则这种试验模型叫古典概型。
例如,掷一次骰子,它的可能结果只有6个,假设骰子是均匀的,则每一种结果出现的可能性都是1/6,所以相等,这种试验是古典概型。
下面介绍古典概型事件的概率的计算公式:
设Ω是古典概型的样本空间,其中样本点总数为n,A为随机事件,其中所含的样本点数为r,则有公式:
例1
掷一次骰子,求点数为奇数点的事件A的概率。
解:样本空间Ω={1,2,3,4,5,6};
A = {1,3,5}
所以 n = 6, r = 3,
P(A) = r/n = 3/6 = 1/2
由于在古典概型中,事件A的概率P(A)的计算公式只需知道样本空间中的样本点的总数n和事件A包含的样本点的个数r就足够,而不必一一列举样本空间的样本点,因此,当样本空间的样本点总数比较多或难于一一列举的时候,也可以用分析的方法求出n与r的数值即可.
例2
从0,1,2,3,4,5,6,7,8,9 这10个数码中,取出三个不同的数码,求所取3个数码不含0和5的事件A的概率。
解:从10个不同数码中,任取3个的结果与顺序无关,所以基本事件总数为: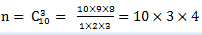
A事件中不能有0和5,所以只能从其余8个数码中任取3个,所以A中的基本事件为: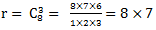
所以根据公式可以计算概率为:
例3-10 略
(四)条件概率
符号P(A|B)叫在事件B已经发生的条件下,事件A发生的概率,叫条件概率,需要指出的是条件概率P(A|B)仍是事件A的概率,但是它有条件,条件是以B已经发生为前提,或者是以B已经发生为条件。
例1
某厂有200名职工,男、女各占一半,男职工中有10人是优秀职工,女职工中有20人是优秀职工,从中任选一名职工。
用A表示所选职工为优秀职工,B表示所选职工是男职工。 求:
(1)P(A);
(2)P(B);
(3)P(AB);
(4)P(A|B)。
解:
1.由本例可以看出 事件A与事件(A|B)不是同一事件,所以它们的概率不同,即事件AB与事件(A|B)也不相同。
2.由本例可以看出
3.本例的结果具有普遍性。下面我们不加证明地给出下面的乘法公式:
例2
在10件产品中,有7件正品,3件次品,从中每次取出一件(不放回),A表示第一次取出正品,B表示第二次取出正品,求:
(1)P(A);
(2)P(B|A);
(3)P(AB)
解:
(1).P(A) = 7/10
(2).P( B|A ) =6/9
(3).P(AB) = P(A)P(B|A) = 7/10 * 6/9 = 7/15
例3
某人寿命为70岁的概率为0.8,寿命为80岁的概率为0.7,若该人现已70岁时,问他能活到80岁的概率是多少?
解:用A表示某人寿命为70岁,B表示某人寿命为80岁。
已知P(A)=0.8,P(B)=0.7
由于A包含B,所以AB=B,P(AB) = P(B) = 0.7;
因为P( B|A ) = P(AB)/P(A) = 0.7/0.8 = 0.875.
所以,已经活到70岁的人能活到80岁的概率为0.875
例4
(五)事件的独立性
定义: 若P(AB)=P(A)P(B),就说事件A与事件B相互独立。
性质1:若A与B独立,则P(A) = P(A|B), P(B) = P(B|A),说明A与B相互独立时,A发生与否,对B发生的概率没有影响,而且,B发生与否也对A发生的概率没有影响。
贝努力重复独立试验概型
引例
某人射击目标的命中率为P,他向目标射击三枪,求这三枪中恰中二枪的概率。
解:用B表示射击三枪,恰中二枪的事件
A1表示第一枪击中目标
A2表示第二枪击中目标
A3表示第三枪击中目标
例1