扔鸡蛋问题
近日刷题刷到了这个问题,LeetCode 887. Super Egg Drop。/584. Drop Eggs II
首先读题就读了很久,还是不能很好的明白题目具体的意思,一搜索才知道这是一道谷歌的经典的面试问题。这也反应出自己的刷题量还是远远不够啊。本文主要是参考了以下两篇文章写成,特此标注。
The Two Egg Problem
【直观算法】Egg Puzzle 鸡蛋难题
文章目录
- 1. 题目描述
- 1.1 求什么?
- 2. 一个鸡蛋的情况
- 3. 无数个鸡蛋的情况
- 4. 两个鸡蛋的情况
- 4.1 树型结构
- 4.2 树的高度最小
- 4.3 每颗子树的高度相等的情况下,树的高度最小
- 5. H层楼,M个鸡蛋
- 5.1 碎掉
- 5.2 没碎
- 5.3 边界条件和初始值
- 5.4 计算顺序
- 5.5 代码1,无优化版本
- 5.6 代码2:下界优化。
1. 题目描述
有栋楼高100层,一个鸡蛋从第x层以上(>x)扔下来会碎,但是从第x层和以下的(<=)的楼层扔下来则不会碎。给定2个鸡蛋,设计一种策略找出x,保证在最坏的情况下,最小扔鸡蛋尝试的次数
1.1 求什么?
找到第x层扔下不会碎,x+1层扔下会碎的临界层所需要的最少的尝试次数r
- 也就是说,我们最后要返回的是保证能找到哦临界层所需要的,最小的尝试次数。
2. 一个鸡蛋的情况
如果我们手上只有一个鸡蛋,同样必须要找到临界层x,一个很容易想到的方法是:从低到高的一层一层的尝试。因为必须保证要找到这样的临界层,所以只能从低到高的尝试
- 首先在第
1层扔,如果没碎,那么继续在第2层扔。 - …
- 这样一层一层的尝试,如果最后在第
x(x < 100)层碎了,那么我们的尝试次数就是x
那么一个鸡蛋的情况下,答案是不是就是x呢?
显然不是,因为我们根本无法判断会在哪一层就碎掉,题目也没有提供这样一个函数接口来判断。这个时候一定要注意题目的描述在最坏的情况下,最小的扔鸡蛋尝试的次数。
思考什么是最坏的情况?假设,我当前的楼层的高度为100,虽然我无法知道在哪一层鸡蛋会碎,但是我知道这个值是一定在1 <= x <= 100的,那么最坏的情况就是在第100层碎掉嘛,那么在这个最坏的情况下,最少的尝试次数肯定也是100次,因为必须要保证找到这个x,我尝试100次,肯定是可以保证找到这个x的。
所以,综上,一个鸡蛋的情况,在最坏的情况下,最少的尝试次数就是楼层的高度
3. 无数个鸡蛋的情况
假设现在有无数个鸡蛋可以使用,或者说有尽可能多的鸡蛋可以使用,这种情况又该怎么分析呢?
因为我现在有无数个鸡蛋可以使用,那我根本就不关系这个鸡蛋碎还是不碎,因为碎了拿一个新的就可以了。那么这个时候,很容易想到二分法的思路。
-
首先拿一个鸡蛋在第
50层扔下来,看是否碎掉- 如果碎了,说明临界层答案一定在
[1,50] - 如果没碎,说明临界层答案一定在
[51,100]
- 如果碎了,说明临界层答案一定在
-
那么不管是否碎掉,临界层答案的空间都缩减了一半。下一次尝试再在子区间的中点进行尝试即可。
-
那么这种方案最坏的情况就是在第
1层碎掉或者在第100层碎掉 -
那么需要尝试的次数为 l o g 2 n log_2n log2n, n n n是楼层高度
-
l o n g 2 100 = 6.644 long_2100 = 6.644 long2100=6.644,那么这里我们应该取
6还是7呢?- 因为我们是要保证在最坏的情况下都要找到这个临界层,所以要向上取整,就是
7次,这里可以简单模拟一下,假设在第100层碎掉,我们按照上面的策略,依此的搜索子区间为: - 假设在第中间层不碎
- [ 1 , 100 ] , [ 51 , 100 ] , [ 76 , 100 ] , [ 89 , 100 ] , [ 95 , 100 ] , [ 98 , 100 ] , [ 100 , 100 ] [1,100],[51,100],[76,100],[89,100],[95,100],[98,100],[100,100] [1,100],[51,100],[76,100],[89,100],[95,100],[98,100],[100,100]
- 那么只需要
7次尝试就能在最坏的情况下完成
- 因为我们是要保证在最坏的情况下都要找到这个临界层,所以要向上取整,就是
-
综上无数个鸡蛋的情况,最坏的情况下最少的尝试次数是 ┌ l o g 2 n ┐ \ulcorner log_2^n \urcorner ┌log2n┐(向上取整), n n n是楼层高度
4. 两个鸡蛋的情况
在理解了一个鸡蛋和无数个鸡蛋的情况的基础上,对于两个鸡蛋我们应该有初步的思路了。我们可以先拿一个鸡蛋出来试错,大致估计出临界层答案所在的区间,然后再利用剩下的一个鸡蛋从低到高一层一层的尝试,这其实就已经退化成了上文中一个鸡蛋的解法。
下面用具体的例子再阐述一下,更方便理解,现在使用鸡蛋1来确定答案可能所在的区间:
-
先在第
50层把鸡蛋1扔下去,那么一定会存在两种结果:- 不碎,那么临界层答案一定在
[51,100],因为没有碎,我们可以继续使用鸡蛋1去缩小答案可能所在的区间,例如接下来在第75层继续扔 - 碎掉,那么临界层答案一定在
[1,50]层,因为现在鸡蛋1碎了,只剩下鸡蛋2可以使用了,那么为了保证能够找到临界层,就需要从第1层到第49层逐层尝试,那么最坏的情况就是到第49层都不碎,那么就选需要尝试49次,加上第50层的尝试,一共就是50次尝试。
- 不碎,那么临界层答案一定在
-
假设在第
75层把鸡蛋扔下去,也肯定存在两种结果:- 不碎,那么临界层答案一定在[76,100]
- 碎了,因为鸡蛋1在第
50层是不碎的,那么临界层答案一定在[51,75],需要从51->74层逐层尝试,假设最坏的情况是到第74层都不碎,那么一共尝试了74-51+1 = 24,再加上第50,75层的尝试,一共尝试了26次。
这里我们需要注意到一个非常重要的点,不管是从多少层扔下去,结果只有两个,碎或者是没碎,这种情况背后就一定是树形结构
数据结构和实际问题想联系的能力,需要加强训练
- 没有分叉,一路推理:线性结构
- 决策结构有分叉:树型结构
- 推理过程中,产生交汇:图结构
所以我们要把上面的尝试转换为树型结构。
4.1 树型结构
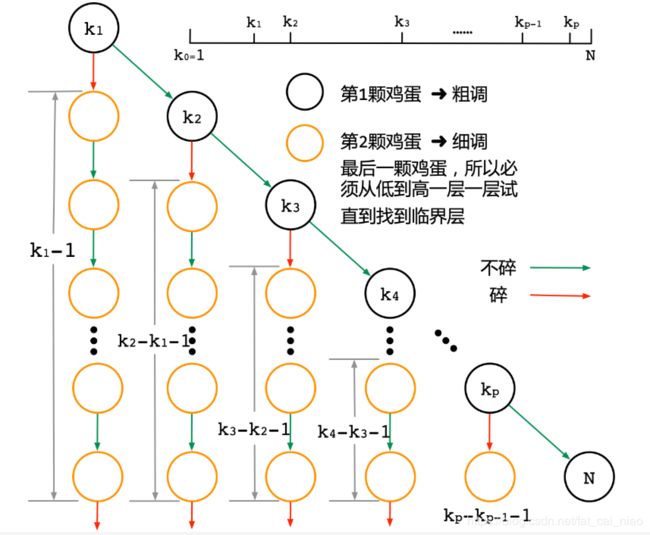
上面的分析,更抽象一点的表达如下,对于鸡蛋1,我们需要选择一个策略,分别在第 K 1 K_1 K1层、 K 2 K_2 K2层、 K 3 K_3 K3层 、 ⋯ \cdots ⋯、 K p K_p Kp层尝试扔鸡蛋,那么在每一层扔,都会有两种结果
-
如果没碎,则继续在第 K i + 1 K_{i+1} Ki+1层继续扔
-
如果碎了,则在区间 [ K i − 1 , K i − 1 ] [K_{i-1},K_{i} - 1] [Ki−1,Ki−1]上用鸡蛋2进行逐层的尝试,(假设 K 0 = 0 K_0=0 K0=0)
-
假设在第 K p K_p Kp层,鸡蛋碎了,那么总的尝试次数就是: K p + K p − K p − 1 − 1 K_p + K_p - K_{p-1} - 1 Kp+Kp−Kp−1−1
-
这里其实很好理解: K p K_p Kp是鸡蛋1的尝试次数, K p − K p − 1 − 1 K_p - K_{p-1} - 1 Kp−Kp−1−1是鸡蛋2的尝试次数
-
从树的角度来理解:这颗树的节点总数一定就是楼层的高度
N -
K p − K p − 1 − 1 K_p - K_{p-1} - 1 Kp−Kp−1−1是鸡蛋2的尝试次数,也是节点 K p K_p Kp的子树的高度
-
求解的目标是总的尝试次数最小,其实就是让树的高度最小
-
那么到这里,问题就变成了,一棵树,在节点总数固定的情况下,树的高度要最小
-
显然,我们可以想到满二叉树是满足这样的性质的。
-
那么接下来的问题就是,如何选择鸡蛋1的策略,也就是如何选择 K 1 , K 2 , ⋯ , K p K_1,K_2, \cdots,K_p K1,K2,⋯,Kp,让树的高度最小
4.2 树的高度最小
上面的叙述中,我们重新定义了问题,是在给定的树节点 K 1 , K 2 , ⋯ , K p K_1,K_2, \cdots,K_p K1,K2,⋯,Kp以及树节点的总数 N N N的前提下,让树的高度最小。
那么怎么才能让树的高度最小呢?尽量让树的形状靠近满二叉树,这里树的高度是重要的问题,我们把每一个策略节点对应的子树的高度罗列一下
- K 1 K_1 K1
- K 2 − K 1 + 1 K_2 - K_1 + 1 K2−K1+1
这里为什么是+1呢?需要解释一下,观察上面的图, K 2 K_2 K2下面的节点数是 K 2 − K 1 − 1 K_2 - K_1 - 1 K2−K1−1,这个值要加上 K 1 K_1 K1和 K 2 K_2 K2这两个节点,所以就是 K 2 − K 1 − 1 + 2 = K 2 − K 1 + 1 K_2 - K_1 - 1 + 2 = K_2 - K_1+ 1 K2−K1−1+2=K2−K1+1,这里再解释一下,为什么 K 2 K_2 K2下面的节点数是 K 2 − K 1 − 1 K_2 - K_1 - 1 K2−K1−1,现在是在 K 2 K_2 K2层碎了,在 K 1 K_1 K1层没碎,那么临界层的答案就在区间 [ K 1 + 1 , K 2 − 1 ] [K_1 + 1, K_2 - 1] [K1+1,K2−1],那么这个区间的节点数量就算 K 2 − 1 − ( K 1 + 1 ) + 1 = K 2 − K 1 − 2 + 1 = K 2 − K 1 − 1 K_2 - 1 - (K_1 + 1) + 1 = K_2 - K_1 - 2 + 1 = K_2 - K_1 -1 K2−1−(K1+1)+1=K2−K1−2+1=K2−K1−1
- K 3 − K 2 + 2 K_3 - K_2 + 2 K3−K2+2
- ⋯ \cdots ⋯
- K p − K p − 1 + p − 1 K_p - K_{p-1} + p-1 Kp−Kp−1+p−1
- N − K p + p N - K_p + p N−Kp+p
4.3 每颗子树的高度相等的情况下,树的高度最小
回想满二叉树,树中每个节点都有左右孩子的情况下树的整体高度最小,那么到这里也一样,只有当子树的高度相等的情况下,树的整体高度才会最小
那么我们就尝试让每颗子树的高度相等。
K 2 − K 1 + 1 = k 1 → K 2 = K 1 + ( K 1 − 1 ) K_2 - K_1 + 1 = k_1\to K_2 = K_1 + (K_1 - 1) K2−K1+1=k1→K2=K1+(K1−1)
K 3 − K 2 + 2 = K 2 − K 1 + 1 → K 3 = 3 K 1 − 3 = K 1 + ( K 1 − 1 ) + ( K 1 − 2 ) K_3 - K_2 + 2 = K_2 - K_1 + 1\to K_3 = 3K_1 - 3 = K_1 + (K_1 - 1) + (K1 - 2) K3−K2+2=K2−K1+1→K3=3K1−3=K1+(K1−1)+(K1−2)
⋯ ⋯ \cdots\cdots ⋯⋯
K p − K p − 1 + p − 1 = K p − 1 + K p − 2 + p − 2 = K 1 + ( K 1 − 1 ) + ( K 1 − 2 ) + ⋯ + ( K 1 − ( p − 1 ) ) K_p - K_{p-1} + p - 1 = K_{p-1} + K_{p-2} + p - 2 = K_1 + (K_1 - 1) + (K_1 - 2) + \cdots + (K_1 - (p - 1)) Kp−Kp−1+p−1=Kp−1+Kp−2+p−2=K1+(K1−1)+(K1−2)+⋯+(K1−(p−1))
K p K_p Kp是鸡蛋1尝试的最后一层,考虑最坏的情况,鸡蛋1应该在第 N N N层要进行尝试,所以鸡蛋1尝试的最后一层一定需要包含第 N N N层。所以:
K 1 + ( K 1 − 1 ) + ( K 1 − 2 ) + ⋯ + 1 ≈ N K_1 + (K_1 - 1) + (K_1 - 2) + \cdots + 1 \thickapprox N K1+(K1−1)+(K1−2)+⋯+1≈N
→ K 1 ( K 1 + 1 ) 2 = N \to \frac{K_1(K_1 + 1)}{2} = N →2K1(K1+1)=N
通过这个等式可以把鸡蛋1尝试的第 K 1 K_1 K1层求解出来,再然后可以把第 K 2 K_2 K2层求解出来,就可以把整个策略都求出来了
当 N = 100 N = 100 N=100,可以求得 K 1 ≈ 13.65 K_1 \thickapprox 13.65 K1≈13.65,这里同样需要向上取整得到 K 1 = 14 K_1 = 14 K1=14。
那么后续的 K i 就 可 以 被 求 解 出 来 了 : K_i就可以被求解出来了: Ki就可以被求解出来了:
K 2 = 14 + ( 14 − 1 ) = 27 K_2 = 14 + (14 - 1) = 27 K2=14+(14−1)=27
K 3 = 14 + ( 14 − 1 ) + ( 14 − 2 ) = 39 K_3 = 14 + (14 - 1) + (14 - 2) = 39 K3=14+(14−1)+(14−2)=39
⋯ \cdots ⋯
依此计算下去可以得到鸡蛋1依此尝试的策略为:
14 , 27 , 39 , 50 , 60 , 69 , 77 , 84 , 90 , 95 , 99 14,27,39,50,60,69,77,84,90,95,99 14,27,39,50,60,69,77,84,90,95,99
当鸡蛋1尝试的策略顶下来了,那么鸡蛋2需要一层一层尝试的层数也就确定下来了,那么总的需要尝试的次数也就可以计算了,我们仍然考虑最坏的请教,在所有可能尝试的次数中取最大的
- 在第 14 14 14层碎掉, r = ( 14 − 1 ) + 1 = 14 r = (14 - 1) + 1 = 14 r=(14−1)+1=14
- 在第 27 27 27层碎掉,$r = (27 - 14 - 1) + 2 = 14 $
- 在第 39 39 39层碎掉, r = ( 39 − 27 − 1 ) + 3 = 14 r = (39 - 27 - 1) + 3 = 14 r=(39−27−1)+3=14
- ⋯ \cdots ⋯
- 在第 99 99 99层碎掉, r = ( 99 − 95 − 1 ) + 11 = 14 r = (99 - 95 - 1) + 11 = 14 r=(99−95−1)+11=14
可以看到,不管在哪一层碎掉,最终需要尝试的次数都是 14 14 14次,这也恰好证明了我们前面求解的正确性,证明了每个子树的高度相同,也就是我们找到了鸡蛋1的扔的策略,让整体的尝试次数最小。
这里可能会有疑问,如果第 99 99 99层没碎呢?那么在第 100 100 100层一定会碎掉,这里再尝试一次即可,那么总的次数加起来一共 11 + 1 = 12 11 + 1 = 12 11+1=12次,是小于 14 14 14次的,但是这不是最坏的情况。
所以综上,给定2个鸡蛋,N层楼高,我们的求解策略是先求出鸡蛋1的尝试策略 K 1 ( K 1 + 1 ) 2 = N \frac{K_1(K_1 + 1)}{2} = N 2K1(K1+1)=N,然后就可以得到整体尝试最少的次数。
5. H层楼,M个鸡蛋
现在考虑更一般的问题。
因为前面的分析,已经让我们可以求解1个鸡蛋H层高,2个鸡蛋H层高的情况了,那么这里,我们就想能不能把鸡蛋的数量减少,减少到我们可以求解的程度,这里鸡蛋数量减少,本质上是把问题规模减少,很容易想到动态规划
假设我们在某一个状态,此时有m个鸡蛋,总共h层高,此时需要在 k ∈ [ 1 , h ] k\in [1,h] k∈[1,h]的范围内选一个 k k k扔下鸡蛋,现在我们要求解的问题可以用符号来表达即 r = f ( h , m ) r = f(h,m) r=f(h,m),具体表示为:在h层高,共m个鸡蛋的情况下,最少的尝试次数。
那么我们就尝试在第 k k k层扔下这个鸡蛋,那么就会有两种情况:
5.1 碎掉
-
那么临界层一定在 [ 1 , k ] [1,k] [1,k],接下来需要在 [ 1 , k − 1 ] [1,k-1] [1,k−1]进行尝试
-
鸡蛋的数量减1,
m = m - 1 -
那么此时我们要求解的问题就变成了: f ( k − 1 , m − 1 ) f(k-1,m-1) f(k−1,m−1),最后的答案为: r = f ( k − 1 , m − 1 ) + 1 r = f(k-1,m-1) + 1 r=f(k−1,m−1)+1
-
此时有一个重要的问题 f ( k − 1 , m − 1 ) f(k-1,m-1) f(k−1,m−1)是可以提前知道吗?我们考虑一种极端的情况,如果 m − 1 = 2 m-1= 2 m−1=2或者 m − 1 = 1 m - 1 = 1 m−1=1,那么这个值就是可以求解的,因此我们是可能提前知道 f ( k − 1 , m − 1 ) f(k-1,m-1) f(k−1,m−1)的
5.2 没碎
- 那么临界层一定在 [ k + 1 , h ] [k+1,h] [k+1,h]
- 鸡蛋的数量不变,仍然是m个
- 那么此时的问题就变成了: f ( h − ( k + 1 ) + 1 , m ) = f ( h − k , m ) f(h - (k+1) + 1,m) = f(h - k,m) f(h−(k+1)+1,m)=f(h−k,m)
- 最后的答案: r = f ( h − k , m ) + 1 r =f(h - k,m) + 1 r=f(h−k,m)+1
那么也就是说,从第k层,扔下,可能存在两种结果,那么我们应该取最大还是最小呢?
- 取最大,因为我们的前提是要在最坏的情况下求尝试次数
- 所以: r = m a x { f ( h − k , m ) , f ( k − 1 , m − 1 ) } + 1 r = max\{f(h - k,m), f(k-1,m-1)\} + 1 r=max{f(h−k,m),f(k−1,m−1)}+1
- 其中这个 k k k的范围是: [ 1 , h ] [1,h] [1,h]。每一层肯定都可以尝试,但是呢,我们求得是最少的尝试次数,所以在不同的 k k k的策略下,我们需要取一个最小值,综合起来,就可以得到完整的状态转移方程:
f ( h , m ) = m i n k ∈ [ 1 , h ] { m a x { f ( h − k , m ) , f ( k − 1 , m − 1 ) } + 1 } f(h,m) = min_{k\in[1,h]} \{max\{f(h - k,m), f(k-1,m-1)\} + 1\} f(h,m)=mink∈[1,h]{max{f(h−k,m),f(k−1,m−1)}+1}
5.3 边界条件和初始值
f ( h , 1 ) = h f(h,1) = h f(h,1)=h
f ( 0 , m ) = 0 f(0,m) = 0 f(0,m)=0
5.4 计算顺序
- 从左往右
- 从小到大
5.5 代码1,无优化版本
这份代码只能在LintCode上AC,无法在LeetCode上AC
class LintCode584 {
public int dropEggs2(int m, int n) {
if (m == 1){
return n;
}
if (n == 0){
return 0;
}
//0. f[i][j] i个鸡蛋j层楼高,最坏情况下,最少的尝试次数
int[][] f = new int[m+1][n+1];
//1, i = 1,1个鸡蛋的时候,最坏情况最少尝试次数就是楼层高度
for (int j = 0; j <= n; j++) {
f[1][j] = j;
}
//2. j = 0, 楼层高度为0,尝试次数肯定为0
for (int i = 1; i <= m; i++) {
f[i][0] = 0;
}
for (int i = 2; i <= m; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = Integer.MAX_VALUE;
//3. 枚举在第k层扔 1->j
for (int k = 1; k <= j; k++) {
//3.1 在第k层碎了,答案在[1,k-1] -->f[i-1][k-1]
//3.2 第k层没碎,答案在[k+1,j],高度为 j - k - 1 + 1 = j-k -->f[i][j-k]
//3.3 在固定k的情况下,考虑 最坏情况,取二者最大值 max
//3.4 在不同的k之间,存在一组最优的策略,让总体尝试次数最小,所以取 min
f[i][j] = Math.min(f[i][j], Math.max(f[i-1][k-1], f[i][j-k]) + 1);
}
}
}
return f[m][n];
}
}
5.6 代码2:下界优化。
上面的代码版本,固定鸡蛋数量m,和楼层高度h,然后在[1,h]逐一尝试
,这一步是可以优化的,是和鸡蛋的数量m有关系的。
回想无数个鸡蛋或者足够多的情况,是可以直接利用二分法来搜索的,答案是 l o g 2 h log_2h log2h
比如此时h=16,m>=4那就不需要再一个一个尝试,直接可以算出r = 4
class LintCode584 {
public int dropEggs2(int m, int n) {
if (m == 1){
return n;
}
if (n == 0){
return 0;
}
//0. f[i][j] i个鸡蛋j层楼高,最坏情况下,最少的尝试次数
int[][] f = new int[m+1][n+1];
//1, i = 1,1个鸡蛋的时候,最坏情况最少尝试次数就是楼层高度
for (int j = 0; j <= n; j++) {
f[1][j] = j;
}
//2. j = 0, 楼层高度为0,尝试次数肯定为0
for (int i = 1; i <= m; i++) {
f[i][0] = 0;
}
for (int i = 2; i <= m; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = Integer.MAX_VALUE;
//3. 判断该当前的鸡蛋数量是否满足足够多,可以使用二分法
// 注意向上取整
int t = (int) Math.ceil((Math.log(j + 1)/Math.log(2)));
if (i >= t){
f[i][j] = t;
}else {
f[i][j] = Integer.MAX_VALUE;
//4. 枚举在第k层扔 1->j
for (int k = 1; k <= j; k++) {
//4.1 在第k层碎了,答案在[1,k-1] -->f[i-1][k-1]
//4.2 第k层没碎,答案在[k+1,j],高度为 j - k - 1 + 1 = j-k -->f[i][j-k]
//4.3 在固定k的情况下,考虑 最坏情况,取二者最大值 max
//4.4 在不同的k之间,存在一组最优的策略,让总体尝试次数最小,所以取 min
f[i][j] = Math.min(f[i][j], Math.max(f[i-1][k-1], f[i][j-k]) + 1);
}
}
}
}
return f[m][n];
}
}