FFT（快速傅里叶变换）算法详解

多项式的点值表示(Point Value Representation)

设多项式的系数表示(Coefficient Representation)：
\[ \begin{align*} \mathrm P_a(x)&=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1} \\ &= \sum_{i=0}^{n-1}a_ix^i \end{align*} \]
则我们对上面的式子可以代入不同的 \(n\) 个 \(x\) 的值，构成一个 \(n\) 维向量：
\[ \begin{bmatrix} \mathrm P_a(x_0) \\ \mathrm P_a(x_1) \\ \mathrm P_a(x_2) \\ \vdots \\ \mathrm P_a(x_{n-1}) \end{bmatrix} = \begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^{n-1} \\ 1 & x_1 & x_1^2 & \cdots & x_1^{n-1} \\ 1 & x_2 & x_2^2 & \cdots & x_2^{n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots & x_{x-1}^{n-1} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{bmatrix} \]
更简洁的写法：
\[ \mathbf P_a = \mathbf X \mathbf \alpha \]
对上式观察后发现，\(\mathbf X\) 是所谓的范德蒙德矩阵(Vandermonde's Matrix)，在 \(n\) 个 \(x\) 的值不同的情况下，其行列式的值为：
\[ \det(\mathbf X) = \prod_{0\leqslant i\lt j \leqslant n-1} (x_j - x_i) \]
很明显，当所有 \(n\) 个 \(x\) 取值不同时，其行列式不为零，因此 \(\mathbf X\) 可逆。
所以我们可以唯一确定多项式系数构成的向量 \(\alpha\)：
\[ \mathbf \alpha = \mathbf X^{-1} \mathbf P_a \]
也就是说，多项式 \(\mathrm P_a(x)\) 还可以由 \(n\) 个 \(x\) 代入得到的 \(n\) 个点值来唯一表示：
\[ \{ \left [x_0, \mathrm P(x_0) \right ], \left [ x_1, \mathrm P(x_1) \right ], \left [x_2, \mathrm P(x_2) \right ], \cdots,\left [ x_{n-1}, \mathrm P(x_{n-1}) \right ] \} \]
这就是多项式的点值表示。

多项式的点值表示是指，对于 \(n\) 次多项式，可以用 \(n\) 个不同的 \(x\) 和与之对应的多项式的值 \(\mathrm P(x)\) 构成一个长度为 \(n\) 的序列，这个序列唯一确定多项式，并且能够与系数表示相互转化。

\(n\) 次单位根

了解了多项式的点值表示，一个很自然的问题是：如何选择 \(x\) 的值，来防止其指数大小爆炸型增长呢？这里可以借用复数的单位根。
简单回顾一下，复数有两种表示方法：迪卡尔积坐标表示和极坐标表示，这里我们用到的是后者：
\[ z=re^{i\theta} \]
\(i\) 是虚数单位，\(r\) 表示模长，\(\theta\) 表示相角。
复数的 \(n\) 次单位根 \(\omega\) 需要满足条件：
\[ \omega^n_n=1 \]
了解复数乘法及其几何意义的同学知道，复数相乘则相角¹相加，相当于复数点逆时针转动；\(n\) 个复数相乘则说明有 \(n\) 个相角相加，\(n\) 次逆时针转动。因此：

\[ \omega_n^n = 1 = e^{i \cdot 2\pi} \]

则 \(n\) 次单位根为：
\[ \sqrt[n] {\omega^n} = e^{i \cdot \frac{2\pi}{n}} \]
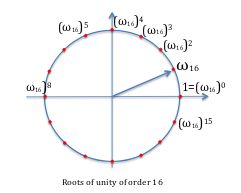
很容易想到，\(n\) 等分 \(2\pi\) 相当于 \(n\) 等分圆。下图是 \(n=16\) 的例子：

引入了 \(n\) 次单位根，我们就可以找到任意 \(n\) 个不同的点值 \(x\)，并且不用担心指数增长带来的大小爆炸性增长的问题。

离散傅里叶变换(Discrete Fourier Transform)及其反变换

DFT

设长度为 \(n\) 的离散序列 \(\alpha^{\mathrm T}=[a_0, a_1, \cdots,a_{n-1}]\)，构建多项式：
\[ \mathrm P_a(x) = \sum_{i=0}^{n-1}a_ix^i = \mathbf x \mathbf \alpha^{\mathrm T} \]
其中，\(\mathbf x^{\mathrm T} = [1, x, x^2, \cdots, x^{n-1}]\)

用 \(n\) 次单位根生成 \(n\) 个不同的值：\(\omega_n^0,\ \omega_n^1,\ \omega_n^2,\ \cdots,\ \omega_n^{n-1}\)
对应的点值表示可以用下面的矩阵运算完成：
\[ \begin{bmatrix} \mathrm P_a(\omega_n^0) \\ \mathrm P_a(\omega_n^1) \\ \mathrm P_a(\omega_n^2) \\ \vdots \\ \mathrm P_a(\omega_n^{n-1}) \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^1 & \omega_n^2 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^4 & \cdots & \omega_n^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{bmatrix} \]
更简洁的写法：
\[ \mathbf P_a = \Omega \alpha \]
序列 \(\mathbf P_a\) 被称为 \(\alpha\) 的离散傅里叶变换(DFT)，也称为频域序列。
很明显，DFT 的计算时间复杂度是 \(O(n^2)\)

IDFT

离散傅里叶反变换，就是根据 DFT 得到的频域序列算出多项式的系数（也称时域序列）。这可以根据单位根矩阵 \(\Omega\) 的逆矩阵 \(\Omega^{-1}\) 得到
\[ \alpha = \Omega^{-1}\mathrm P_a \]
一般来说，计算矩阵的逆的时间复杂度高达 \(O(n^3)\)。所幸，单位根矩阵的逆 \(\Omega^{-1}\) 有个优良的性质可以省去庞大的计算量：
\[ \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^1 & \omega_n^2 & \cdots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^4 & \cdots & \omega_n^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \cdots & \omega_n^{(n-1)(n-1)} \end{bmatrix}^{-1} = \frac 1 n \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^{-1} & \omega_n^{-2} & \cdots & \omega_n^{-(n-1)} \\ 1 & \omega_n^{-2} & \omega_n^{-4} & \cdots & \omega_n^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{-(n-1)} & \omega_n^{-2(n-1)} & \cdots & \omega_n^{-(n-1)(n-1)} \end{bmatrix} \]
也就是说，求 \(\Omega^{-1}\) 就是将里面元素的指数改成其相反数，再对所有元素除以 \(n\)。
有了这个性质，我们就可以得到：
\[ \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{n-1} \end{bmatrix}=\frac1 n \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega_n^{-1} & \omega_n^{-2} & \cdots & \omega_n^{-(n-1)} \\ 1 & \omega_n^{-2} & \omega_n^{-4} & \cdots & \omega_n^{-2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega_n^{-(n-1)} & \omega_n^{-2(n-1)} & \cdots & \omega_n^{-(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} \mathrm P_a(\omega_n^0) \\ \mathrm P_a(\omega_n^1) \\ \mathrm P_a(\omega_n^2) \\ \vdots \\ \mathrm P_a(\omega_n^{n-1}) \end{bmatrix} \]
很明显，DFT 和 IDFT 的计算时间复杂度都是 \(O(n^2)\)，效率并不高。

快速傅里叶变换(Fast Fourier Transform)及其反变换

FFT

FFT 是用分治法（Divide & Conquer）的思想，用来优化 DFT 计算矩阵相乘的时间复杂度过高这一问题的算法。
设 \(n\) 次多项式 \(\mathrm P(x)\)²：

\[ \mathrm P(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_{n-1}x^{n-1} \]

我们把多项式 \(\mathrm P(x)\) 按照系数下标的奇偶性分成两部分
\[ \mathrm P_{e}(x^2) = a_0 + a_2x^2 + a_4\left(x^2\right)^2 + \cdots + a_{n-2}x^{n-2} \\ x\mathrm P_{o}(x^2) = x\left [a_1 + a_3x^2+a_5\left(x^2\right)^2+\cdots+a_{n-1}x^{n-2} \right ] \]
则多项式 \(\mathrm P(x)\) 就是奇偶两部分之和
\[ \mathrm P(x)=\mathrm P_e(x^2)+x\mathrm P_o(x^2) \]
从上式中可以看出，多项式 \(\mathrm P(x)\) 可以由两个系数个数为 \(n/2\) 的多项式 \(\mathrm P_{e}(x^2)\) 和 \(\mathrm P_o(x^2)\) 计算得到。
对于 \(\mathrm P_e(x^2)\) 和 \(\mathrm P_{o}(x^2)\)，我们令 \(x=x^2\)，就会发现这很明显是一个递归的过程：
\[ \mathrm P_{e}(x)=a_0+a_2x+a_4x^2+\cdots+a_{n-2}x^{\frac{n-2}{2}} \\ \mathrm P_{ee}(x^2)=a_0+a_4x^2+a_8x^4+\cdots+a_{n-4}x^{\frac{n-2}{2}-1} \\ x\mathrm P_{eo}(x^2)=x\left [ a_2+a_6x^2+a_{10}x^4+\cdots+a_{n-2}x^{\frac{n-2}{2}-1} \right ] \\ \]
就可以求出
\[ \mathrm P_e(x)=\mathrm P_{ee}(x^2)+xP_{eo}(x^2) \]
同理
\[ \mathrm P_{o}(x)=a_1+a_3x+a_5x^2+\cdots+a_{n-1}x^{\frac{n-2}{2}} \\ \mathrm P_{oe}(x^2)=a_1+a_5x^2+a_9x^4+\cdots+a_{n-3}x^{\frac{n-2}{2}-1} \\ x\mathrm P_{oo}(x^2)=x\left [ a_3+a_7x^2+a_{11}x^4+\cdots+a_{n-1}x^{\frac{n-2}{2}-1} \right ] \]
同样可以求出
\[ \mathrm P_o(x)=\mathrm P_{oe}(x^2)+xP_{oo}(x^2) \]
递归的终止条件很明显，就是当遇到多项式中只有一个系数时返回该系数。
因此我们将 \(n\) 个单位根 \(\omega_n^0,\ \omega_n^1,\ \omega_n^2,\ \cdots,\ \omega_n^{n-1}\) 带入多项式 \(\mathrm P(x)\)：
\[ \mathrm P(\omega_n^{k})=\mathrm P_e(\omega_n^{2k})+\omega_n^k\mathrm P_o(\omega_n^{2k}) \quad (k=0, 1, \cdots,n-1) \]
刚刚提到，多项式 \(\mathrm P_{e}(x^2)\) 和 \(\mathrm P_o(x^2)\) 的系数个数为 \(n/2\) ，恰好 \(n\) 个单位根平方后也只剩下 \(n/2\) 个不同的单位根，简单证明如下：

首先证明：
\[ \left( \omega_n^k \right)^2=e^{i\frac{2\pi k}{n}\cdot2}=e^{i\frac{2\pi k}{n/2}}=\omega_{n/2}^k \]
因此相当于 \(n\) 等分圆变成了 \(n/2\) 等分圆。下面证明 \(k=0,\ 1,\ \cdots,\ \frac n 2-1\)：
设 \(k_1=m\), \(k_2=m+n/2\)，\(m=0,1,\cdots,\frac{n}{2}-1\)。则
\[ \omega_{n/2}^{k_{1}} = \omega_{n/2}^{m}=e^{i\frac{2\pi m}{n/2}} \\ \omega_{n/2}^{k_2} = \omega_{n/2}^{m+n/2}=e^{i\frac{2\pi (m+n/2)}{n/2}}=e^{i\left(\frac{2\pi m}{n/2}+2\pi{}\right)}=e^{i\frac{2\pi m}{n/2}} \]
即：
\[ \omega_{n/2}^{m}=\omega_{n/2}^{m+n/2}\quad (m=0,1,\cdots,\frac n 2-1) \]
由此可以说明，\(\omega_n^k\) 是周期序列，其最小正周期为 \(n/2\)。因此 \(k=0, 1, \cdots, \frac n 2 -1\)

因此多项式 \(\mathrm P(\omega_n^{k})\) 可改写为
\[ \mathrm P(\omega_n^{k})=\mathrm P_e(\omega_{n/2}^{k})+\omega_n^k\mathrm P_o(\omega_{n/2}^{k}) \quad (k=0, 1, \cdots,\frac n 2-1) \]
从上式中可以看出，计算 \(\mathrm P_e(\omega_{n/2}^{k})\) 和 \(\mathrm P_o(\omega_{n/2}^{k})\) 各需要 \(n/2\) 次乘法运算，即一共 \(n\) 次乘法运算；而计算\(\mathrm P_{ee}(\omega_{n/4}^{k})\) 、 \(\mathrm P_{eo}(\omega_{n/4}^{k})\) 、\(\mathrm P_{oe}(\omega_{n/4}^k)\) 和 \(\mathrm P_{oo}(\omega_{n/4}^k)\) 各需要 \(n/4\) 次乘法运算，即一共 \(n\) 次乘法运算……以此类推，这种每层递归规模减半的递归深度很明显是 \(\log n\)，因此 FFT 算法的时间复杂度就是 \(O(n\log n)\)

IFFT

快速傅里叶变换反变换同样是优化 IDFT 计算矩阵相乘的时间复杂度。由于 DFT 和 IDFT 核心操作一样，都是矩阵相乘，因此 FFT 和 IDFT 的核心操作就是利用分治的思想减少矩阵相乘的运算量。可以想到，FFT 的过程可以直接移植到 IFFT 中来，需要修改的两个地方是

1. 单位根指数部分改成其相反数：\(\omega_n^{-k}\)
2. 得到的结果均除以 \(n\)

因此，IFFT 的时间复杂度也是\(O(n\log n)\)

---

Refer: COMP3121/9101, CSE UNSW
Written with StackEdit.

---

1. 本文相角一律用弧度表示。↩

2. 这里为了推导过程的整洁，假设 \(n\) 是 2 的整数次幂。这个假设的合理性在于：即使 \(n\) 不是 2 的整数次幂，我们也可以在多项是后面后面补零达到离 \(n\) 最近的下一个 2 的整数次幂。↩

转载于:https://www.cnblogs.com/LexLuc/p/10597868.html