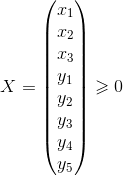单纯形法求解线性规划问题
1、生产组织与计划问题
某电视机厂生产I、II、III型号的电视机,按照市场需求,三种型号的电视机每天产量最少为200、250、100,该厂每天可以利用的总工时为1000个时间单位(小时),可利用的材料每天有2000个单位,每个产品工时消耗为2、1.2、1,原材料消耗为1、1.5、4,每台电视产生的利润分别为10、14、12,问每种型号的产量如何调配能够使工厂的利润获得最大化?
2、解答
2.1、列出目标函数与约束条件
工厂的目标利润可以用如下公式表达
![]()
工厂生产计划的约束条件可以表达如下
![]()
![]()
![]()
![]()
![]()
![]()
2.2、将线性规划一般模型转化成标准形式
对于目标函数中的极大值求解,在标准形式中应改写成极小值求解
![]()
对于约束条件中的≤,应引进松弛变量,使其转化为等式(相对的≥应引入剩余变量)
![]()
![]()
![]()
![]()
![]()
对于自由变量应该通过拆解或者抵消的办法进行处理,因为本问题中没有自由变量,因此对自由变量无需处理,直接copy如下
![]() ,
,![]()
提取公式中的相关向量矩阵
![]()
2.3、对线性规划标准形式进行分块
调整矩阵 A 和 X 的列,并分解,矩阵A分解为基B与非基N的组合
变量X分解为基变量XB与非基变量XN
2.4、求解初始的基本可行解
显然的B是可行基,X=(inv(B)*b ;0)是该线性规划问题的一个初始基本可行解(当线性规划问题中不存在该松弛项时候可以通过添加人工变量的方法构造初始可行解,人造变量对应的列组成人造基),此时工厂的产量为0.利润为0
2.5 迭代寻优
在此基本可行解的基础上进行不断的换基操作,直到求得最优解,求解过程如一下程序所示
clc
clear all
close all
syms x1 x2 x3 y1 y2 y3 y4 y5;
m = 5;
% 根据例题构造线性规划(LP)的标准方程
C = [0 0 0 0 0 -10 -14 -12];
A = [1 0 0 0 0 1 1.5 4;0 1 0 0 0 2 1.2 1;0 0 -1 0 0 1 0 0;...
0 0 0 -1 0 0 1 0; 0 0 0 0 -1 0 0 1];
b = [2000 ;1000 ;200 ;250 ;100];
X = [y1 y2 y3 y4 y5 x1 x2 x3].';
% 将标准方程中的系数矩阵A分解成基B与非基N,将X分解为基变量XB与非基变量XN
B = A(1:m,1:m);
N = A(1:m,m+1:end);
CB = C(1,1:m);
CN = C(1,m+1:end);
XB = X(1:m,:);
XN = X(m+1:end,:);
invB = pinv(B);
% XB = invB*b - invB*N*XN
% 令XN = zeros(3,1).'构造方程的一个基本解Xbasic
% invBxb >= 0时候,称B是Lp的可行基,此时Xbasic是Lp的基本可行解
invBxb = invB*b;
Xbasic = [invBxb ; zeros(3,1)];
%{
% 验证C*X 是否等于 CB*invB*b + (CN - CB*invB*N)*XN
C*X
CB*invB*b + (CN - CB*invB*N)*XN
%}
% 验证基本可行解是否是LP的最优解,当creterion>=0时候,Xbasic是最优解,B是最优基
creterion = C - CB*invB*A;
% 将LP转写称为典式形式y00\Ym\invBxN\invBxb,Y0n是LP的检验数(相对成本系数)
% minS= y00 + y0n*XN
% s.t : XB = invBxb - invBxN*XN
% X>=0
y00 = CB*invB*b;
Y0n = CN - CB*invB*N;
invBxN = invB*N;
% 构造方程的单纯形表
disp('构造LP的单纯形表')
TableLP = [0 0 X.';0 -y00 zeros(1,m) Y0n;XB invBxb eye(m) invBxN];
disp(TableLP)
while(min(TableLP(2,2+m+1:end)) < 0)
% 对TableLP中第二行非基部分进行判断,如果有负数元素,则认为当前解不是最优解
% 然后判断invBxN的元素与0的关系,全<=0时候没有最优解,当存在>0的元素时候,执行
% 换基操作,循环迭代直至最优解(为更具普适性,可以改用bland规则进行判断换基)
qPosition = find(TableLP(2,2+m+1:end) < 0,1);
% 取q所在列为主列,判断主列元素全部<=0是否成立,若成立则方程没有最优解,计算结束
if(max(TableLP(3:end,2 + m +qPosition)) < 0)
disp('LP方程没有最优解');
break;
else
% 若不成立继续换基操作
yi0 = TableLP(3:end,2);
yiq = TableLP(3:end,2+m+qPosition);
theta = min(yi0(yiq>0)./yiq(yiq>0));
Jp = find(yi0./yiq == theta,1);
% 取Jp所在行为主行,并以ypq为主元继续进行换基操作,xq为进基,xp为出基
ypq = TableLP(2+Jp,2+m+qPosition);
TableLP(2 + Jp,1) = TableLP(1,2 + m + qPosition);
TableLP(2+Jp,2:end) = TableLP(2+Jp,2:end)/ypq;
for i = 1:m+1
if(i ~= Jp + 1)
TableLP(i + 1,2:end) = TableLP(i + 1,2:end) - TableLP(Jp + 2,2:end)*...
TableLP(i + 1,2 + m + qPosition);
end
end
end
disp('更新单纯形表')
disp(TableLP)
end
2.5 结果分析
构造LP的单纯形表
[ 0, 0, y1, y2, y3, y4, y5, x1, x2, x3]
[ 0, 0, 0, 0, 0, 0, 0, -10, -14, -12]
[ y1, 2000, 1, 0, 0, 0, 0, 1, 3/2, 4]
[ y2, 1000, 0, 1, 0, 0, 0, 2, 6/5, 1]
[ y3, -200, 0, 0, 1, 0, 0, -1, 0, 0]
[ y4, -250, 0, 0, 0, 1, 0, 0, -1, 0]
[ y5, -100, 0, 0, 0, 0, 1, 0, 0, -1]
更新单纯形表
[ 0, 0, y1, y2, y3, y4, y5, x1, x2, x3]
[ 0, 5000, 0, 5, 0, 0, 0, 0, -8, -7]
[ y1, 1500, 1, -1/2, 0, 0, 0, 0, 9/10, 7/2]
[ x1, 500, 0, 1/2, 0, 0, 0, 1, 3/5, 1/2]
[ y3, 300, 0, 1/2, 1, 0, 0, 0, 3/5, 1/2]
[ y4, -250, 0, 0, 0, 1, 0, 0, -1, 0]
[ y5, -100, 0, 0, 0, 0, 1, 0, 0, -1]
更新单纯形表
[ 0, 0, y1, y2, y3, y4, y5, x1, x2, x3]
[ 0, 9000, 0, 35/3, 40/3, 0, 0, 0, 0, -1/3]
[ y1, 1050, 1, -5/4, -3/2, 0, 0, 0, 0, 11/4]
[ x1, 200, 0, 0, -1, 0, 0, 1, 0, 0]
[ x2, 500, 0, 5/6, 5/3, 0, 0, 0, 1, 5/6]
[ y4, 250, 0, 5/6, 5/3, 1, 0, 0, 0, 5/6]
[ y5, -100, 0, 0, 0, 0, 1, 0, 0, -1]
更新单纯形表
[ 0, 0, y1, y2, y3, y4, y5, x1, x2, x3]
[ 0, 9100, 0, 12, 14, 2/5, 0, 0, 0, 0]
[ y1, 225, 1, -4, -7, -33/10, 0, 0, 0, 0]
[ x1, 200, 0, 0, -1, 0, 0, 1, 0, 0]
[ x2, 250, 0, 0, 0, -1, 0, 0, 1, 0]
[ x3, 300, 0, 1, 2, 6/5, 0, 0, 0, 1]
[ y5, 200, 0, 1, 2, 6/5, 1, 0, 0, 0]根据计算结果,可知:
三种型号的产量分别应该为 200 250 300,可以获得最大利润
Max(S) = 10*x1 + 14*x2 + 12*x3 = 9100 元