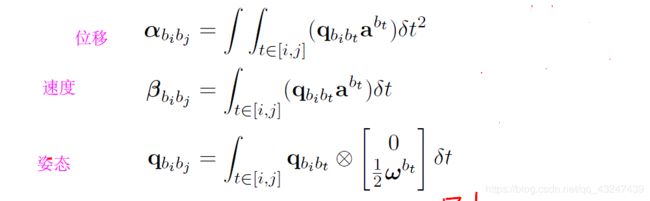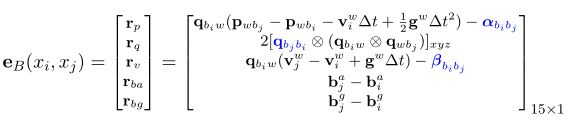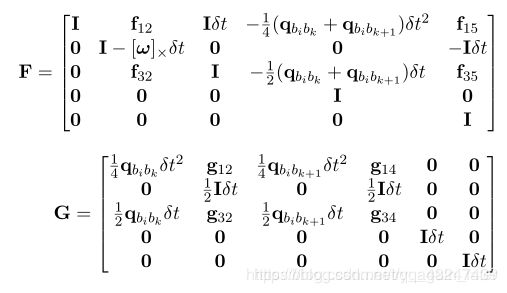VINS-mono 代码解析——IMU预积分processIMU( )实现
文章目录
- 前言
- 一 processIMU()函数
- 1 IMU 预积分IntegrationBase类
- 2 push_back()函数
- 3 evaluate()函数
- 4 propagate()函数
- 5 中值积分midPointIntegration()
- 6 repropagate()新的bias重新计算预积分
- 7 imu_factor.h
前言
在VINS-mono中,estimator/src/estimator_node.cpp中,从主函数依次为:
main( )---->process( )---->processIMU( )
其中,processIMU( )函数的原型为:
void Estimator::processIMU(double dt, const Vector3d &linear_acceleration, const Vector3d &angular_velocity)
一 processIMU()函数
// IMU预积分,中值积分得到当前PQV作为 优化 初值
void Estimator::processIMU(double dt, const Vector3d &linear_acceleration, const Vector3d &angular_velocity)
{
// 1.判断是不是第一个imu消息,如果是第一个imu消息,则将当前传入的线加速度和角速度作为初始的加速度和角速度
if (!first_imu)
{
first_imu = true;
acc_0 = linear_acceleration;
gyr_0 = angular_velocity;
}
// 2.IMU 预积分类对象还没出现,创建一个对象
if (!pre_integrations[frame_count])
{
pre_integrations[frame_count] = new IntegrationBase{acc_0, gyr_0, Bas[frame_count], Bgs[frame_count]};
}
//当frame_count==0的时候表示滑动窗口中还没有图像帧数据,不需要进行预积分,只进行线加速度和角速度初始值的更新
if (frame_count != 0)
{
// 3.预积分操作
pre_integrations[frame_count]->push_back(dt, linear_acceleration, angular_velocity);
//if(solver_flag != NON_LINEAR)
tmp_pre_integration->push_back(dt, linear_acceleration, angular_velocity);
// 4.dt、加速度、角速度加到buf中
dt_buf[frame_count].push_back(dt);
linear_acceleration_buf[frame_count].push_back(linear_acceleration);
angular_velocity_buf[frame_count].push_back(angular_velocity);
int j = frame_count;
// 5.采用的是中值积分的传播方式
Vector3d un_acc_0 = Rs[j] * (acc_0 - Bas[j]) - g;// a0=Q(a^-ba)-g 已知上一帧imu速度
Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - Bgs[j];// w=0.5(w0+w1)-bg
Rs[j] *= Utility::deltaQ(un_gyr * dt).toRotationMatrix();
Vector3d un_acc_1 = Rs[j] * (linear_acceleration - Bas[j]) - g;// a1 当前帧imu速度
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);// 中值积分下的加速度a=1/2(a0+a1)
Ps[j] += dt * Vs[j] + 0.5 * dt * dt * un_acc;// P=P+v*t+1/2*a*t^2
Vs[j] += dt * un_acc;// V=V+a*t
}
// 6.当frame_count==0的时候表示滑动窗口中还没有图像帧数据,不需要进行预积分,只进行线加速度和角速度初始值的更新
acc_0 = linear_acceleration;
gyr_0 = angular_velocity;
}
1 IMU 预积分IntegrationBase类
预积分类:加速度计、陀螺仪、线性加速度计ba、陀螺仪bg、雅克比矩阵初始化、协方差矩阵15*15、dt、PVQ
IntegrationBase() = delete;
IntegrationBase(const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
: acc_0{_acc_0}, gyr_0{_gyr_0}, linearized_acc{_acc_0}, linearized_gyr{_gyr_0},
linearized_ba{_linearized_ba}, linearized_bg{_linearized_bg},
jacobian{Eigen::Matrix<double, 15, 15>::Identity()}, covariance{Eigen::Matrix<double, 15, 15>::Zero()},
sum_dt{0.0}, delta_p{Eigen::Vector3d::Zero()}, delta_q{Eigen::Quaterniond::Identity()}, delta_v{Eigen::Vector3d::Zero()}
{
noise = Eigen::Matrix<double, 18, 18>::Zero();
noise.block<3, 3>(0, 0) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(3, 3) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(6, 6) = (ACC_N * ACC_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(9, 9) = (GYR_N * GYR_N) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(12, 12) = (ACC_W * ACC_W) * Eigen::Matrix3d::Identity();
noise.block<3, 3>(15, 15) = (GYR_W * GYR_W) * Eigen::Matrix3d::Identity();
}
2 push_back()函数
void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{
dt_buf.push_back(dt);
acc_buf.push_back(acc);
gyr_buf.push_back(gyr);
//进入预积分阶段
propagate(dt, acc, gyr);
}
3 evaluate()函数
Eigen::Matrix<double, 15, 1> evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
{
Eigen::Matrix<double, 15, 1> residuals;// 残差
Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);
Eigen::Vector3d dba = Bai - linearized_ba;
Eigen::Vector3d dbg = Bgi - linearized_bg;
Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg);
Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg;
Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg;
residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
return residuals;//上面的都是为了写residuals
}
4 propagate()函数
IMU预积分传播方程
积分计算两个关键帧之间IMU测量的变化量:
旋转delta_q 速度delta_v 位移delta_p
加速度的biaslinearized_ba 陀螺仪的Bias linearized_bg
同时维护更新预积分的Jacobian和Covariance,计算优化时必要的参数
预积分传播方程,在预积分传播方程propagate中使用中点积分方法midPointIntegration计算预积分的测量值,中点积分法中主要包含两个部分,分别是得到状态变化量result_delta_q,result_delta_p,result_delta_v,result_linearized_ba,result_linearized_bg和得到跟新协方差矩阵和Jacobian矩阵(注意,虽然得到了雅各比矩阵和协方差矩阵,但是还没有求残差和修正偏置一阶项的状态变量),由于使用的是中点积分,所以需要上一个时刻的IMU数据,包括测量值加速度和角速度以及状态变化量,初始值由构造函数提供。需要注意的是这里定义的delta_p等是累积的变化量,也就是说是从i时刻到当前时刻的变化量,这个才是最终要求的结果(为修正偏置一阶项),而result_delta_q等只是一个暂时的变量,最后残差和雅可比矩阵、协方差矩阵保存在pre_integrations中,还有一个函数这里暂时还没有用到,是在优化的时候才被调用的,但是其属于预积分的内容,evaluate函数在这个函数里面进行了状态变化量的偏置一阶修正以及残差的计算。
步骤2预积分公式(3)未考虑误差,提供imu计算的当前旋转,位置,速度,作为优化的初值
求状态向量对bias的Jacobian,当bias变化较小时,使用Jacobian去更新状态;否则需要以当前imu为参考系,重新预积分,对应repropagation()。同时,需要计算error state model中误差传播方程的系数矩阵F和V.最主要的还是在midPointIntegration()函数中。
//进入预积分阶段
/**
* 预计分计算
* _dt 时间间隔
* _acc_1 线加速度
* _gyr_1 角速度
*/
void propagate(double _dt, const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1)
{
dt = _dt;
acc_1 = _acc_1;
gyr_1 = _gyr_1;
Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
//中点积分方法
midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
linearized_ba, linearized_bg,
result_delta_p, result_delta_q, result_delta_v,
result_linearized_ba, result_linearized_bg, 1);
//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
// linearized_ba, linearized_bg);
//更新PQV
delta_p = result_delta_p;
delta_q = result_delta_q;
delta_v = result_delta_v;
//更新偏置
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
delta_q.normalize();
//时间进行累加
sum_dt += dt;
//预积分完后,更新当前的线加速度和角速度为上一时刻的线加速度和角速度
acc_0 = acc_1;
gyr_0 = gyr_1;
}
5 中值积分midPointIntegration()
IMU预积分中采用中值积分递推Jacobian和Covariance
构造误差的线性化递推方程,得到Jacobian和Covariance递推公式-> Paper 式9、10、11
/**
* 该函数是以中值点的方式进行预积分求解PVQ的,需要注意的是这里使用的是离散形式的预积分公式
* 参数中_0代表上次测量值,_1代表当前测量值,delta_p,delta_q,delta_v代表相对预积分初始参考系的位移,旋转四元数,以及速度
* 从k帧预积分到k+1帧,则参考系是k帧的imu坐标系
*/
void midPointIntegration(double _dt,
const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1,
const Eigen::Vector3d &delta_p, const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,
const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,
Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v,
Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, bool update_jacobian)
{
//ROS_INFO("midpoint integration");
//delta_q为相对预计分参考系的旋转四元数,线加速度的测量值减去偏差然后和旋转四元数相乘表示将线加速度从世界坐标系下转到了body(IMU)坐标系下
Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
//计算平均角速度
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
//对平均角速度和时间的乘积构成的旋转值组成的四元数左乘旋转四元数,获得当前时刻body中的旋转向量(四元数表示)
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);
//用计算出来的旋转向量左乘当前的加速度,表示将线加速度从世界坐标系下转到了body坐标系下
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
//计算两个时刻的平均加速度
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
//当前的位移:当前位移=前一次的位移+(速度×时间)+1/2×加速度的×时间的平方
//匀加速度运动的位移公式:s_1 = s_0 + v_0 * t + 1/2 * a * t^2
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;
//速度计算公式:v_1 = v_0 + a*t
result_delta_v = delta_v + un_acc * _dt;
// 预积分的过程中Bias并未发生改变,所以还保存在result当中
result_linearized_ba = linearized_ba;
result_linearized_bg = linearized_bg;
//是否更新IMU预计分测量关于IMU Bias的雅克比矩阵
if(update_jacobian)
{
//计算平均角速度
Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
//计算_acc_0这个观测线加速度对应的实际加速度
Vector3d a_0_x = _acc_0 - linearized_ba;
//计算_acc_1这个观测线加速度对应的实际加速度
Vector3d a_1_x = _acc_1 - linearized_ba;
Matrix3d R_w_x, R_a_0_x, R_a_1_x;
/**
* | 0 -W_z W_y |
* [W]_x = | W_z 0 -W_x |
* | -W_y W_x 0 |
*/
R_w_x<<0, -w_x(2), w_x(1),
w_x(2), 0, -w_x(0),
-w_x(1), w_x(0), 0;
R_a_0_x<<0, -a_0_x(2), a_0_x(1),
a_0_x(2), 0, -a_0_x(0),
-a_0_x(1), a_0_x(0), 0;
R_a_1_x<<0, -a_1_x(2), a_1_x(1),
a_1_x(2), 0, -a_1_x(0),
-a_1_x(1), a_1_x(0), 0;
//F是一个15行15列的数据类型为double,数据全部为0的矩阵,Matrix创建的矩阵默认按列存储
MatrixXd F = MatrixXd::Zero(15, 15);
/**
* matrix.block(i,j, p, q) : 表示返回从矩阵(i, j)开始,每行取p个元素,每列取q个元素所组成的临时新矩阵对象,原矩阵的元素不变;
* matrix.block(i, j) :可理解为一个p行q列的子矩阵,该定义表示从原矩阵中第(i, j)开始,获取一个p行q列的子矩阵,
* 返回该子矩阵组成的临时矩阵对象,原矩阵的元素不变;
*/
//从F矩阵的(0,0)位置的元素开始,将前3行3列的元素赋值为单位矩阵
/**
* 下面F和V矩阵为什么这样构造,是需要进行相关推导的。这里的F、V矩阵的构造理解可以参考论文附录中给出的公式
*/
F.block<3, 3>(0, 0) = Matrix3d::Identity();
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt +
-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt;
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt;
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt;
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt +
-0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
//cout<<"A"<
MatrixXd V = MatrixXd::Zero(15,18);
V.block<3, 3>(0, 0) = 0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) = 0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) = 0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) = V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) = 0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) = 0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) = 0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) = V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;
//step_jacobian = F;
//step_V = V;
/**
* 求矩阵的转置、共轭矩阵、伴随矩阵:可以通过成员函数transpose()、conjugate()、adjoint()来完成。注意:这些函数返回操作后的结果,
* 而不会对原矩阵的元素进行直接操作,如果要让原矩阵进行转换,则需要使用响应的InPlace函数,如transpoceInPlace()等
*/
//雅克比jacobian的迭代公式:J_(k+1)=F*J_k,J_0=I
jacobian = F * jacobian;
/**
* covariance为协方差,协方差的迭代公式:P_(k+1) = F*P_k*F^T + V*Q*V^T,P_0 = 0
* P_k就是协方差,Q为noise,其初值为18*18的单位矩阵
*/
covariance = F * covariance * F.transpose() + V * noise * V.transpose();
}
}
6 repropagate()新的bias重新计算预积分
// 新的bias重新计算预积分
void repropagate(const Eigen::Vector3d &_linearized_ba, const Eigen::Vector3d &_linearized_bg)
{
sum_dt = 0.0;
acc_0 = linearized_acc;// 旧的加速度和陀螺仪
gyr_0 = linearized_gyr;
delta_p.setZero();
delta_q.setIdentity();
delta_v.setZero();
linearized_ba = _linearized_ba;// 更新Bias
linearized_bg = _linearized_bg;
jacobian.setIdentity();
covariance.setZero();
for (int i = 0; i < static_cast<int>(dt_buf.size()); i++)
propagate(dt_buf[i], acc_buf[i], gyr_buf[i]);
}
7 imu_factor.h
主函数为
virtual bool Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
// 1、优化变量:i和j时刻的4组优化变量参数块
Eigen::Vector3d Pi(parameters[0][0], parameters[0][1], parameters[0][2]);
Eigen::Quaterniond Qi(parameters[0][6], parameters[0][3], parameters[0][4], parameters[0][5]);
Eigen::Vector3d Vi(parameters[1][0], parameters[1][1], parameters[1][2]);
Eigen::Vector3d Bai(parameters[1][3], parameters[1][4], parameters[1][5]);
Eigen::Vector3d Bgi(parameters[1][6], parameters[1][7], parameters[1][8]);
Eigen::Vector3d Pj(parameters[2][0], parameters[2][1], parameters[2][2]);
Eigen::Quaterniond Qj(parameters[2][6], parameters[2][3], parameters[2][4], parameters[2][5]);
Eigen::Vector3d Vj(parameters[3][0], parameters[3][1], parameters[3][2]);
Eigen::Vector3d Baj(parameters[3][3], parameters[3][4], parameters[3][5]);
Eigen::Vector3d Bgj(parameters[3][6], parameters[3][7], parameters[3][8]);
2、构建IMU残差residual
主要通过调用 pre_integration->evaluate,预积分模块中evaluate函数。也就是上面的3 evaluate()函数
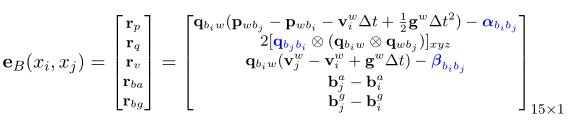

// 2、构建IMU残差residual
Eigen::Map<Eigen::Matrix<double, 15, 1>> residual(residuals);// 已知残差
residual = pre_integration->evaluate(Pi, Qi, Vi, Bai, Bgi,
Pj, Qj, Vj, Baj, Bgj);
// LLT分解,residual 还需乘以信息矩阵的sqrt_info
// 因为优化函数其实是d=r^T P^-1 r ,P表示协方差,而ceres只接受最小二乘优化
// 因此需要把P^-1做LLT分解,使d=(L^T r)^T (L^T r) = r'^T r
Eigen::Matrix<double, 15, 15> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose();
residual = sqrt_info * residual;
3、获取预积分的误差递推函数中pqv关于ba、bg的Jacobian
// 3、获取预积分的误差递推函数中pqv关于ba、bg的Jacobian
double sum_dt = pre_integration->sum_dt;
Eigen::Matrix3d dp_dba = pre_integration->jacobian.template block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = pre_integration->jacobian.template block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = pre_integration->jacobian.template block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = pre_integration->jacobian.template block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = pre_integration->jacobian.template block<3, 3>(O_V, O_BG);
if (pre_integration->jacobian.maxCoeff() > 1e8 || pre_integration->jacobian.minCoeff() < -1e8)
{
ROS_WARN("numerical unstable in preintegration");
//std::cout << pre_integration->jacobian << std::endl;
/// ROS_BREAK();
}
接下来便是对4个模块进行求解
4、第i帧的IMU位姿 pbi、qbi
// 4、第i帧的IMU位姿 pbi、qbi
if (jacobians[0])
{
Eigen::Map<Eigen::Matrix<double, 15, 7, Eigen::RowMajor>> jacobian_pose_i(jacobians[0]);
jacobian_pose_i.setZero();
jacobian_pose_i.block<3, 3>(O_P, O_P) = -Qi.inverse().toRotationMatrix();
jacobian_pose_i.block<3, 3>(O_P, O_R) = Utility::skewSymmetric(Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt));
#if 0
jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Qj.inverse() * Qi).toRotationMatrix();
#else
Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
jacobian_pose_i.block<3, 3>(O_R, O_R) = -(Utility::Qleft(Qj.inverse() * Qi) * Utility::Qright(corrected_delta_q)).bottomRightCorner<3, 3>();
#endif
jacobian_pose_i.block<3, 3>(O_V, O_R) = Utility::skewSymmetric(Qi.inverse() * (G * sum_dt + Vj - Vi));
jacobian_pose_i = sqrt_info * jacobian_pose_i;
if (jacobian_pose_i.maxCoeff() > 1e8 || jacobian_pose_i.minCoeff() < -1e8)
{
ROS_WARN("numerical unstable in preintegration");
//std::cout << sqrt_info << std::endl;
//ROS_BREAK();
}
}
5、第i帧的imu速度vbi、bai、bgi
// 6、第i帧的imu速度vbi、bai、bgi
if (jacobians[1])
{
Eigen::Map<Eigen::Matrix<double, 15, 9, Eigen::RowMajor>> jacobian_speedbias_i(jacobians[1]);
jacobian_speedbias_i.setZero();
jacobian_speedbias_i.block<3, 3>(O_P, O_V - O_V) = -Qi.inverse().toRotationMatrix() * sum_dt;
jacobian_speedbias_i.block<3, 3>(O_P, O_BA - O_V) = -dp_dba;
jacobian_speedbias_i.block<3, 3>(O_P, O_BG - O_V) = -dp_dbg;
#if 0
jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -dq_dbg;
#else
//Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
//jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * corrected_delta_q).bottomRightCorner<3, 3>() * dq_dbg;
jacobian_speedbias_i.block<3, 3>(O_R, O_BG - O_V) = -Utility::Qleft(Qj.inverse() * Qi * pre_integration->delta_q).bottomRightCorner<3, 3>() * dq_dbg;
#endif
jacobian_speedbias_i.block<3, 3>(O_V, O_V - O_V) = -Qi.inverse().toRotationMatrix();
jacobian_speedbias_i.block<3, 3>(O_V, O_BA - O_V) = -dv_dba;
jacobian_speedbias_i.block<3, 3>(O_V, O_BG - O_V) = -dv_dbg;
jacobian_speedbias_i.block<3, 3>(O_BA, O_BA - O_V) = -Eigen::Matrix3d::Identity();
jacobian_speedbias_i.block<3, 3>(O_BG, O_BG - O_V) = -Eigen::Matrix3d::Identity();
jacobian_speedbias_i = sqrt_info * jacobian_speedbias_i;
//ROS_ASSERT(fabs(jacobian_speedbias_i.maxCoeff()) < 1e8);
//ROS_ASSERT(fabs(jacobian_speedbias_i.minCoeff()) < 1e8);
}
6、第j帧的IMU位姿 pbj、qbj
// 7、第j帧的IMU位姿 pbj、qbj
if (jacobians[2])
{
Eigen::Map<Eigen::Matrix<double, 15, 7, Eigen::RowMajor>> jacobian_pose_j(jacobians[2]);
jacobian_pose_j.setZero();
jacobian_pose_j.block<3, 3>(O_P, O_P) = Qi.inverse().toRotationMatrix();
#if 0
jacobian_pose_j.block<3, 3>(O_R, O_R) = Eigen::Matrix3d::Identity();
#else
Eigen::Quaterniond corrected_delta_q = pre_integration->delta_q * Utility::deltaQ(dq_dbg * (Bgi - pre_integration->linearized_bg));
jacobian_pose_j.block<3, 3>(O_R, O_R) = Utility::Qleft(corrected_delta_q.inverse() * Qi.inverse() * Qj).bottomRightCorner<3, 3>();
#endif
jacobian_pose_j = sqrt_info * jacobian_pose_j;
//ROS_ASSERT(fabs(jacobian_pose_j.maxCoeff()) < 1e8);
//ROS_ASSERT(fabs(jacobian_pose_j.minCoeff()) < 1e8);
}
7、第j帧的IMU速度vbj、baj、bgj
// 8、第j帧的IMU速度vbj、baj、bgj
if (jacobians[3])
{
Eigen::Map<Eigen::Matrix<double, 15, 9, Eigen::RowMajor>> jacobian_speedbias_j(jacobians[3]);
jacobian_speedbias_j.setZero();
jacobian_speedbias_j.block<3, 3>(O_V, O_V - O_V) = Qi.inverse().toRotationMatrix();
jacobian_speedbias_j.block<3, 3>(O_BA, O_BA - O_V) = Eigen::Matrix3d::Identity();
jacobian_speedbias_j.block<3, 3>(O_BG, O_BG - O_V) = Eigen::Matrix3d::Identity();
jacobian_speedbias_j = sqrt_info * jacobian_speedbias_j;
//ROS_ASSERT(fabs(jacobian_speedbias_j.maxCoeff()) < 1e8);
//ROS_ASSERT(fabs(jacobian_speedbias_j.minCoeff()) < 1e8);
}