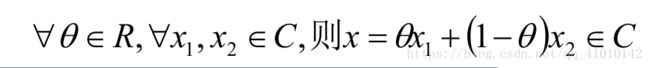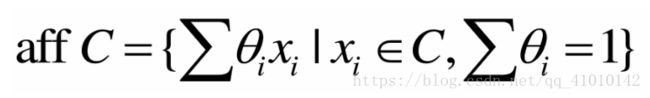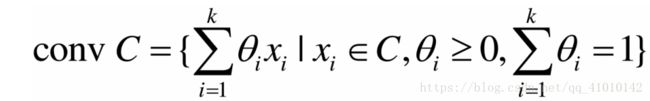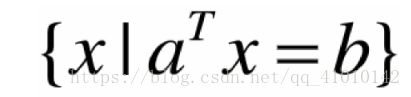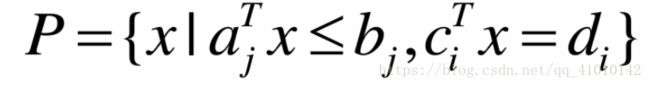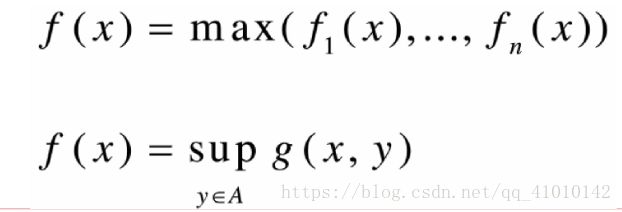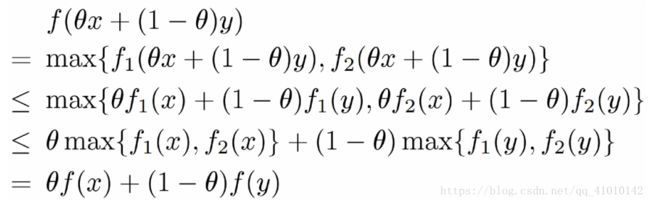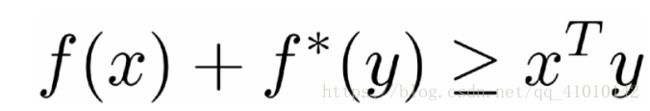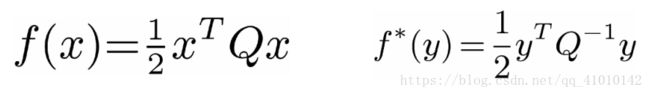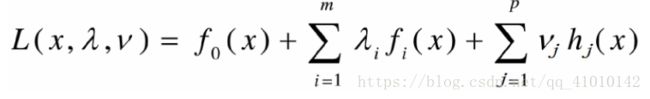数学基础（三）——凸优化

                                        凸优化

ps: 个人笔记 根据视频和PDF学习

思考凸集和凸函数

y=x 2 是凸函数，函数图像上位于y=x 2 上方的区域构成凸集。
    凸函数图像的上方区域，一定是凸集；
    一个函数图像的上方区域为凸集，则该函数是凸函数。
    稍后给出上述表述的形式化定义。

因此，学习凸优化，考察凸函数，先从凸集及其性质开始。

(超)几何体的向量表达

给定二维平面上两个定点：a(x 1 ,y 1 )，b(x 2 ,y 2 )，则：
     直线:x=θa + (1-θ)b, θ∈R
     线段:x=θa + (1-θ)b, θ∈[0,1]
 一般的，f(x,y)=0表示定义域在R 2 的曲线
        特殊的，y=g(x)表示定义域在R的曲线，f(x,y)=y-g(x)
一般的，f(x,y,z)=0表示定义域在R 3 的曲面
        特殊的，z=h(x,y)表示定义域在R 2 的曲面，f(x,y,z)=z-h(x,y)
上述表达方式可以方便的推广到高维
        记x=(u 1 ,u 2 ,…u n )，则f(x)=0表示定义域在R n 的超曲面。

        不特殊说明，后面将使用x1表示向量，如：定义两个点x1,x2,则x=θx1 + (1-θ)x2, θ∈R表示经过这两点的直线

仿射集(Affine set)

定义：通过集合C中任意两个不同点的直线仍然在集合C内，则称集合C为仿射集。

仿射集的例子：直线、平面、超平面
    超平面：Ax=b
    f(x)=0表示定义域在R n 的超曲面：令f(x)=Ax-b，则f(x)=0表示“截距”为-b的超平面。
    三维空间的平面是二维的；四维空间的平面是几维的？
        n维空间的n-1维仿射集为n-1维超平面。

    后面将继续考察超平面的定义。

仿射包

仿射包：包含集合C的最小仿射集。

仿射维数： 仿射包的维数。
    三角形的仿射维数为2
    线段的仿射维数为1

    球的仿射维数为3

内点和相对内点

给定一个集合C，如何定义哪些点在“边界”上，哪些点在内部？
     直观的想法：对于集合C中的某个点x，以x为中心做半径为r的球(r>0，且非常小)，若球和C的交集完全落在C的内部(即：是C的子集)，则x为C的内点。

    将该概念用在C的仿射集aff C上，则为相对内点。一般用relint C表示C的相对内点。

B(x,r)表示以x为球心，r为半径做一个球。affC是仿射包

举例

PS：这里C的内点是空的，理解为X3=0,相当于一个瓶是空的，或者说没有厚度，所以说是空的

凸集

集合C内任意两点间的线段均在集合C内，则称集合C为凸集。

仿射集和凸集的关系

因为仿射集的条件比凸集的条件强，所以，仿射集必然是凸集。

凸集

ps:上面正方形有些边界没有，不是凸集

凸包

集合C的所有点的凸组合形成的集合，叫做集合C的凸包。

集合C的凸包是能够包含C的最小的凸集。

凸包的例子

PS：凸包最后会变成一个凸型

锥(Cones)

锥的举例：过原点的射线、射线族、角

第一张图是凸锥；第二张图不是凸的；第三张图是凸锥

锥包

PS：锥包的话最后会变成一个锥型

超平面和半空间

超平面hyperplane

半空间halfspace

几何表示：

欧式球和椭球

欧式球

椭球

范数球和范数锥(欧式空间的推广)

范数

范数球

范数锥

R 3 空间中的二阶锥

多面体

多面体有限个半空间和超平面的交集。

仿射集(如超平面、直线)、射线、线段、半空间都是多面体。
多面体是凸集。
此外：有界的多面体有时称作多胞形(polytope)。
    注：该定义略混乱，不同文献的含义不同。

多面体是凸集的表示：

PS：分别小于这些超平面，组成一个多面体，线是要无限延伸的

保持凸性的运算

集合交运算
仿射变换
    函数f=Ax+b的形式，称函数是仿射的：即线性函数加常数的形式
透视变换

投射变换(线性分式变换)

集合交运算：半空间的交

仿射变换

仿射变换

    伸缩、平移、投影

若f是仿射变换，

    若S为凸集，则f(S)为凸集；

    若f(S)为凸集，则S为凸集。

进一步分析仿射变换

两个凸集的和为凸集

u(x) = x*x,     u(y) = y*y,    v(x,y) = x*x + y*y

两个凸集的笛卡尔积(直积)为凸集

两个集合的部分和为凸集(分配率)

透视变换

透视函数对向量进行伸缩(规范化)，使得最后一维的分量为1并舍弃之。

透视的直观意义
    小孔成像

红色的点是二维的，通过孔成像后变成蓝点,是一维的了

透视变换的保凸性

凸集的透视变换仍然是凸集。

思考：反过来，若某集合的透视变换是凸集，这个集合一定是凸集吗？

投射函数(线性分式函数)

投射函数是透视函数和仿射函数的复合。

g为仿射函数：

定义f为线性分式函数

若c=0,d>0，则f即为普通的仿射函数。

投射的作用

分割超平面

设C和D为两不相交的凸集，则存在超平面P，P可以将C和D分离。

注意上式中可以取等号。
    “若两个凸集C和D的分割超平面存在，C和D不相交”为假命题。

      加强条件：若两个凸集至少有一个是开集，那么当且仅当存在分割超平面，它们不相交。

分割超平面表示：

分割超平面的构造

两个集合的距离，定义为两个集合间元素的最短距离。

做集合C和集合D最短线段的垂直平分线。

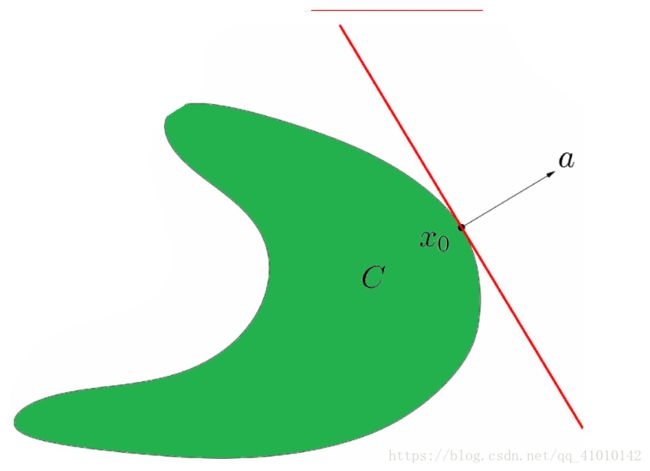
支撑超平面

设集合C，x0为C边界上的点。若存在a≠0，满足对任意x∈C，都有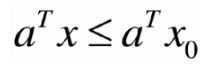 

成立，则称超平面 为集合C在点x0处的支撑超平面。

凸集边界上任意一点，均存在支撑超平面。

若一个闭的非中空集合，在边界上的任意一点存在支撑超平面，则该集合为凸集。

支撑超平面表示：
注意：图中C不是凸集

但如果C的边界上任何点都存在支撑超平面，则C是凸集。

凸函数

若函数f的定义域domf为凸集，且满足

一阶可微

若f一阶可微，则函数f为凸函数当前仅当f的定义域domf为凸集，且

进一步的思考

结合凸函数图像和支撑超平面理解该问题
对于凸函数，其一阶Taylor近似本质上是该函数的全局下估计。
反之，如果一个函数的一阶Taylor近似总是起全局下估计，则该函数是凸函数。

该不等式说明从一个函数的局部信息，可以得到一定程度的全局信息。

二阶可微

若函数f二阶可微，则函数f为凸函数当前仅当dom为凸集，且

若f是一元函数，上式表示二阶导大于等于0

若f是多元函数，上式表示二阶导Hessian矩阵半正定。

凸函数举例

上境图

函数f的图像定义为：

函数f的上境图(epigraph)定义为：

凸函数与凸集

一个函数是凸函数，当且仅当其上境图是凸集。
    思考：如何证明？(提示：定义)

进一步，一个函数是凹函数，当且仅当其亚图(hypograph)是凸集。

⭐Jensen不等式：若f是凸函数

基本Jensen不等式

保持函数凸性的算子

凸函数的非负加权和

凸函数与仿射函数的复合

凸函数的逐点最大值、逐点上确界

凸函数的逐点最大值

f1,f2均为凸函数，定义函数f：

则函数f为凸函数。

思考

逐点上确界和上境图的关系
    一系列函数逐点上确界函数对应着这些函数上境图的交集。
    Oxy平面上随意画N条直线，在每个x处取这些直线的最大的点，则构成的新函数是凸函数。
    点x到任意集合C的最远距离     
        f是凸函数
        证明：范数是凸的(思考：为什么？)，逐点求上界，仍然是凸的。

共轭函数

原函数 的共轭函数定义：

显然，定义式的右端是关于y的仿射函数，它们逐点求上确界，得到的函数f*(y)一定是凸函数。
该名称的原因：

    凸函数的共轭函数的共轭函数是其本身。

对共轭函数的理解

如果函数f可微，在满足f'(x)=y的点x处差值最大。

例：求共轭函数

可逆对称阵Q，对于任意的向量x，定义函数f：

关于(x,y)的函数

在 时取上确界，带入，得到：

f*即是f的共轭函数

Fenchel不等式

根据定义

立刻可以得到：

Fenchel不等式的应用

根据f(x)及其共轭函数f*(x)

带入Fenchel不等式，得到：

凸优化

优化问题的基本形式

优化问题的基本形式

优化问题的域

可行点(解)(feasible)
    x∈D，且满足约束条件
可行域(可解集)
    所有可行点的集合

最优化值

最优化解

局部最优问题

凸优化问题的基本形式

其中，f i (x)为凸函数，h j (x)为仿射函数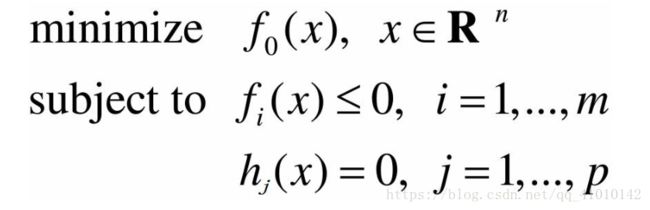

凸优化问题的重要性质
凸优化问题的可行域为凸集

凸优化问题的局部最优解即为全局最优解

非凸优化问题的变形

对偶问题

一般优化问题的Lagrange乘子法

Lagrange函数

    对固定的x，Lagrange函数L(x,λ,v)为关于λ和v的仿射函数

Lagrange对偶函数(dual function)

Lagrange对偶函数

若没有下确界，定义：
根据定义，显然有：对∀λ>0，∀v，若原优化问题有最优值p*，则

进一步：Lagrange对偶函数为凹函数。

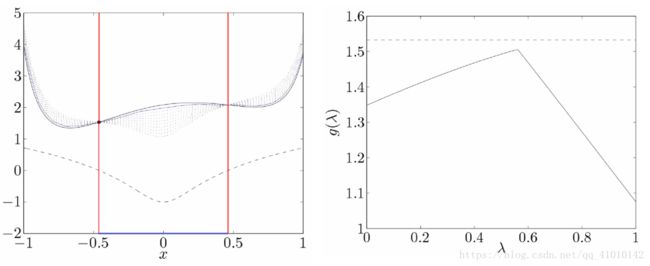
左侧为原函数，右侧为对偶函数

线性方程的最小二乘问题

原问题

Lagrange函数

Lagrange对偶函数

    对L求x的偏导，带入L
    对g求v的偏导

强对偶条件

若要对偶函数的最大值即为原问题的最小值，考察需要满足的条件：

Karush-Kuhn-Tucker (KKT)条件