信息安全数学基础（第二版陈恭亮）答案

---

写在前头： 自己写的题目，计算题答案基本都是对的，证明题过程有些不准确，大家可以根据助教点评的思路自己修改。

第一章 2 4 6 8 13 28 32

（2）证明：如果a是整数，则a³-a被3整除。

（4）证明：任意三个连续整数的乘积都被6整除。

（6）证明：191，547都是素数，而737，747都是合数。

（8）问是否存在这样的整数a,b,c,使得a|bc, 但ab,ac。

（13）证明：形如4k+3的素数有无穷多个。

助教点评：在验证整除性的过程中最好把具体验算过程写出来
最后一题的构造不是特别理想，但证明的很完整（q是4k+1形式的数其实不需要讨论，因为与我们的假设没有太大关系）
　
针对上述(2)~(13)

（28）求以下整数对的最大公因数：
①（55,85）

②（202,282）

③（666,1414）

④（20785,44350）

（32）运用广义欧几里除法求整数s,t使得s * a + t * b=(a,b)
①（1613,3589）

②（2947,3772）

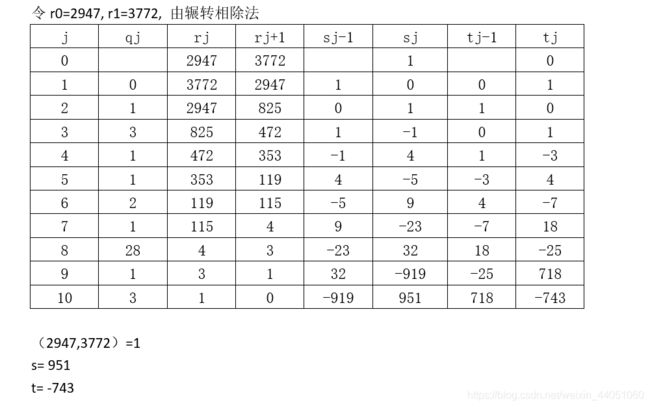
③（20041,37516）

④（1107,822916）

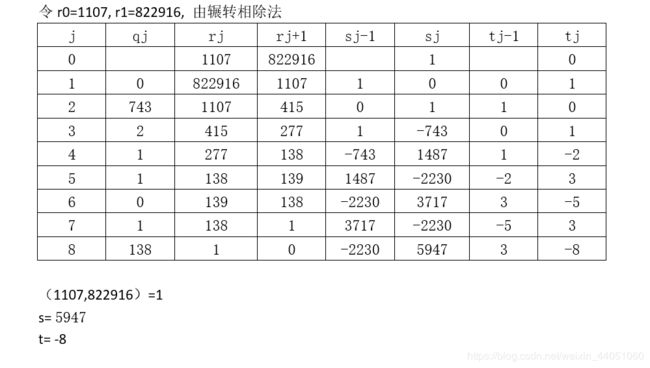
第二章 1 2 14 24 31

（1）
①写出模9的一个完全剩余系，它的每个数是奇数

②写出模9的一个完全剩余系，它的每个数是偶数

③ ①②中的要求对模10的完全剩余系能实现吗？

（2）证明：当m>2时，0²,1²，… ，(m-1)²一定不是模m的完全剩余系。

助教点评：(1)③最好用数学语言去表述，可以利用反证法推出全部是偶数或奇数假设不成立，这样说明可能更好，思路正确！

（14）证明：如果a^k≡b^k(mod m),a^k+1≡b^k+1(mod m)， 这里a,b,k,m是整数，k>0,m>0,并且(a,m)=1，那么a≡b(mod m)，如果去掉(a,m)=1这个条件，结果仍成立吗？

（24）计算3^1000000（mod 7）

（31）证明：如果c₁,c₂,…,c_φ(m)是模m的简化剩余系，那么c₁+c₂+…+c_φ(m)≡ 0(mod m),m>2

助教点评：(14)最好给出一个具体的反例
(31)简化剩余系中元素个数为什么必定是偶数呢，这点需要证明

第三章 1 7 11 19 24

（1）求出下列一次同余方程的所有解。
① 3x≡2(mod 7)

② 6x≡3(mod 9)

③ 17x≡14(mod 21)

④ 15x≡9(mod 25)

（7）运用Euler定理求解下列一次同余方程。
① 5x≡3(mod 14)

② 4x≡7(mod 15)

③ 3x≡5(mod 16)

（11）证明：同余方程组

X≡b₁(mod m₁)
X≡b₂(mod m₂)
….
X≡b_k(mod m_k)

的解是
X≡b₁M₁^ϕ(m1)+b₂M₂^ϕ(m2)+…+b_k*M_k^ϕ(mk)(mod m)
这里m_j两两互素,m=m₁m₂…m_k，M_j=m/m_j，j=1,2,…k。

（19）将同余式方程化为同余式组来求解。
(i) 23x≡1(mod 140)


(ii) 17x≡229(mod 1540)



（24）求解同余式f(x)≡x⁴+7x+4≡0(mod 243)

第四章 1 2 9 20 23 25 27 38

（1）求模p=13，23，31，37，47的二次剩余和二次非剩余



（2）求满足方程E：y²=x³-3x+1（mod 7）的所有点

（9）求解同余式x²≡39（mod 105）

（20）

① （17/37）

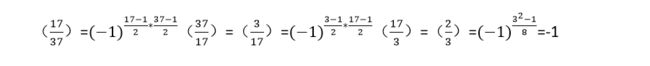
②（151/373）

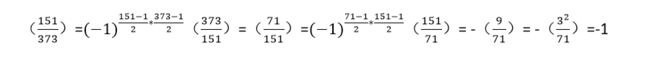
③（191/397）

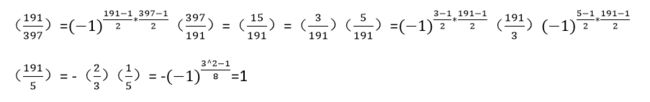
④（911/2003）

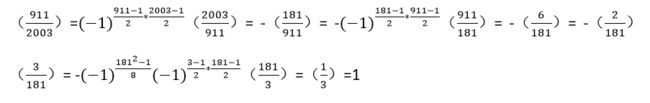
⑤（37/200723）

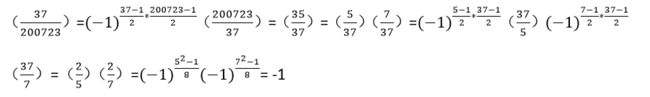
⑥（7/20040803）

（23）设p是奇素数，p∤a，证明：存在正整数u，v，(u,v)=1，使得u²+av²≡0(mod p)的充要条件是-a是模p的二次剩余。

（25）设p是奇素数，且p≡1(mod 4)。证明：
（i）1,2,…,(p-1)/2中模P的二次剩余与二次非剩余的个数均为(p-1)/4个

（ii）1,2,…, (p-1)中有(p-1)/4个偶数为模P的二次剩余，(p-1)/4个奇数为模P的二次剩余

（iii）1,2,…, (p-1)中有(p-1)/4个偶数为模P的二次非剩余，(p-1)/4个奇数为模P的二次非剩余

（iv）1,2,…,(p-1)中全体模P的二次剩余之和等于p(p-1)/4

（v）1,2,…,(p-1)中全体模P的二次非剩余之和等于p(p-1)/4

助教点评：（25）最好用(p-a/p)和(a/p)的关系去说明可能更清晰

（27）证明：下列形式的素数均有无穷多个，8k-1,8k+3,8k-3


（38）设q=281,求解下列同余式
(i） x²≡2（mod q）

(ii） x²≡3（mod q）

(iii）x²≡5（mod q）

(iv）x²≡7（mod q）

(v）x²≡11（mod q）

助教点评：（38）三道有解的题目均漏了一解，二次同余式的解通常是成对出现的，书上的例题写的不完整，要把p-x补上

第五章 5 7 9 10 11 12

（5）问模47的原根有多少个？求出模47的所有原根。

（7）设m>1是整数，a是与m互素的整数，假如ord_m（a）=st，那么ord_m（a^s）=t。

（9）设m=aⁿ-1，其中a和n是正整数，证明：ord_m（a）=n，从而得到n|φ（m）。

（10）设p和(p-1)/2都是素数，设a是与p互素的正整数，如果a≢1，a²≢1，a^(p-1)/2≢1（mod p）,则a是模p的原根。

（11）求模113的原根。

（12） 求模113²的原根。