算法丨带内外边界的三角剖分算法(Delaunay)
关于三角剖分算法,网上现有的其实说的还是挺明白的,可以参考https://www.cnblogs.com/zhiyishou/p/4430017.html
不过在此我有几点要补充:
自身对该算法流程的理解
(1) 构建超级三角形
(2) 将所有的点按照x从小到大排序
(3) While循环将每一个点依次加入,加点后会出现三种情况:
·此点在外接圆内:将这个外接圆的三角形从temp中删除,并且将所有的边加入edge buffer中(注意,如果edge buffer中已存在此边,不仅不要再次加入,还要把这条边从edge buffer中删除)
·此点在外接圆外侧,并且在右侧(即该点的横坐标-圆心横坐标>R):该三角形是Delaunay三角形,加入triangle中,并将这个三角形从temp中删除
·此点在外接圆外侧,并且在左侧:不进行处理,也不将这个三角形从temp中删除
(注意:edge buffer每次循环都要清空)
(4)最后将temp和triangle合并,并将含超级三角形三个点的三角形删除
有关优化(?)问题
这些博客几乎都提到了排序优化问题,但是怎么优化?怎么排序?我看了好久也没找到答案(也可能是我瞎x
其实我觉得大佬们不提可能是觉得挺明显易懂的,没有必要单独列出来,我理解的排序优化就是将所有的点按照X坐标的从小到大排序(即将所有的点从左到右排序),如果不进行排序的话,那么这一步就会出现问题:
如果该点在外接圆的右侧
则该三角形为Delaunay三角形,保存到triangles
并在temp里去除掉有关三角剖分内外边界的问题
关于这个我下了一个ppt,上面有记录思想(可以参考,但是我没有按照这个办法做出来):
1. 进行标准的Delaunay三角剖分,即不考虑点的性质进行剖分。剖分结果为T1。
2.对T1进行追踪分析寻找约束边界,对未在剖分中的三角形采用中点插入算法恢复约束边界,
结果为T2。
步骤如下:
(1) 依次取出内孔的一条约束边界,设为AB,直到所有内孔约束边界取完为止。
(2) 在T1的剖分结果中进行查询以判断AB是否在T1的三角形边集中已经存在,如果存在,则转向(1)。
(3) 设AB的中点为C,将C点作为附加点插入网格,重新构造新的DT网格,结果为T11。
(4) 在T11的剖分结果中进行查询AC,BC是否已经在T11的三角形边集中,直至AB边完全被DT所包含,然后转向(1)
3. 对T2约束边界内的多余线段进行边界裁减
(1) 顺序取出内约束边界链表中的一个边界点,设为K1,如果边界链表为空,则退出。
(2) 在内约束边界链表中取出K2,K2≠K1且K2不为K1的邻接边界点,如果边界链表为空,则转向(1)。
(3) 判断K1K2在T2是否存在,如果存在,且过K1K2的中点的水平射线与内约束边界的交点有奇数个,则从T2中删除包含K1K2边的所有三角形,否则转向(2)。
我总结后,步骤如下:
(1)遍历边界,如果结果三角形中包含该边界,则找下一条边界,如果不包含该边界,进入(2)。
(2)将与此边界相交的三角形(相交点不为三角形的顶点,且不为该边界线的起点和终点)删除,并且将这些相交三角形的点都存下来。然后将这些点按照边界的左边还是右边分两半,然后进行基于凹凸顶点判定的简单三角形剖分(关于这个算法详情可见上面的论文)。
内边界外边界基本一样。
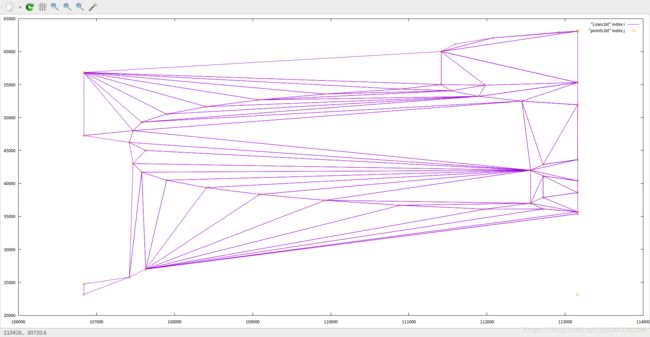
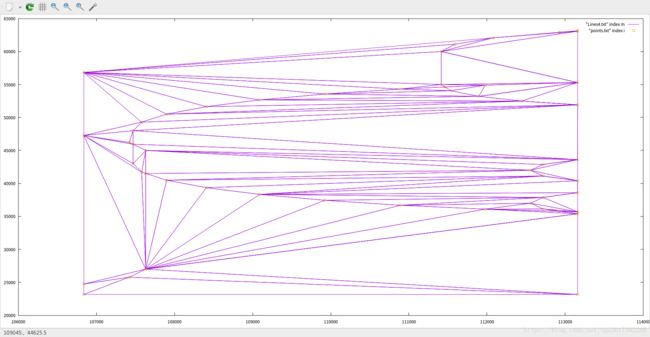
然后成果图:
(改了快两周qwq,唉……如果再有问题还得再改……otz)
最后几个小提示吧(其实查一下也能查到):
关于凹凸顶点判定中如何将点逆时针存下来,可以借鉴凸包算法,即:拿出y坐标最小的点,然后按照点到该y最小点的度数大小升序排序(若度数相同,则按照里y最小点的远近升序排序)
关于点是否在三角形外,我借鉴了https://blog.csdn.net/firehotest/article/details/62698595这篇博客,但是在一个地方会出现问题,即三角形三个点和想要判断的点几乎共线时,会出错…(然后我自己粗暴地改了下,但不知道会不会出现问题,所以关于这个地方要注意下)
关于如何算点的凹凸性,我是借鉴了一篇论文,但是找不到了(苦笑),上网上查吧,应该是有的(关于这个地方,我可能会出现一个错误,即三点共线,那么中间的点是凹点还是凸点)