双连通分量模板以及对一些不好理解点的解释
双连通分量(biconnected component, 简称bcc)概念:
双连通分量有点双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点(一条边)都不会改变此图的连通性,即不存在割点(桥),则称作点(边)双连通图。一个无向图中的每一个极大点(边)双连通子图称作此无向图的点(边)双连通分量。求双连通分量可用Tarjan算法。--百度百科
先学一下tarjan算法以及求割点割边的算法之后,再看会比较好理解一些。(1.Tarjan 2.图的割点割边)
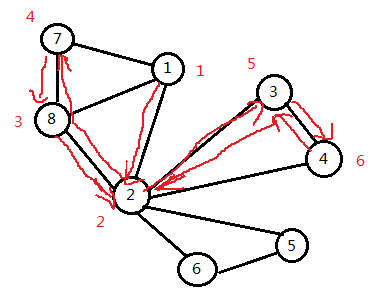
先看比较难写点双连通分量的求法,直接看代码理解。另附图一张:
Code:
#include
using namespace std;
const int maxn = 110;
const int maxm = 10010;
struct node
{
int u, v, next;
}edge[maxm], tp;
int n, m; //点数,边数
int head[maxn], no;
int add_bcc[maxn];//去掉该点之后能增加的bcc数目
int index; //时间戳
int yltd; //图的初始连通分量
int num[maxn], low[maxn];//时间戳和能回到的最早时间戳
int iscut[maxn];//是否为割点
int bccno[maxn], bcc_cnt; //bccno[i]表示i属于哪个bcc
stack S; //存储bcc边
vector bcc[maxn];
inline void init()
{
no = 0;
memset(head, -1, sizeof head);
}
inline void add(int u, int v)
{
edge[no].u = u; edge[no].v = v;
edge[no].next = head[u]; head[u] = no++;
edge[no].u = v; edge[no].v = u;
edge[no].next = head[v]; head[v] = no++;
}
inline void input()
{
int u, v;
for(int i = 1; i <= m; ++i)
{
scanf("%d %d", &u, &v);
add(u, v);
}
}
void tarjan(int cur, int father)
{
int child = 0;
num[cur] = low[cur] = ++index;
int k = head[cur];
while(k != -1)
{
int v = edge[k].v;
if(!num[v])
{
S.push(edge[k]);
++child;
tarjan(v, cur);
low[cur] = min(low[cur], low[v]);
if(low[v] >= num[cur])
//把更节点看做普通的节点,对根节点这个条件是一定满足的,
//可以实现把回溯到根节点剩下的出栈,其实这就是一个新的双连通分量
{
iscut[cur] = 1;
++add_bcc[cur];
++bcc_cnt;//准备把新的双连通分量加入bcc
bcc[bcc_cnt].clear();
while(true)
{
tp = S.top(); S.pop();
if(bccno[tp.u] != bcc_cnt)
{
bcc[bcc_cnt].push_back(tp.u);
bccno[tp.u] = bcc_cnt;
}
if(bccno[tp.v] != bcc_cnt)
{
bcc[bcc_cnt].push_back(tp.v);
bccno[tp.v] = bcc_cnt;
}
if(tp.u == edge[k].u && tp.v == edge[k].v) break;
}
}
}
else if(num[v] < num[cur] && edge[k].v != father)
{
//num[v] < num[cur]的判断是为了防止当前cur为割点,然后它刚访问的一个双连通分量里有一个较深的点
//访问过了。然后再从cur访问,如果不判断就会将这个点加入S,造成错误,见上图。
//可以看到时间戳走到6再次回溯到2时,还能通过2对2-4这条边进行一次尝试,不判断的话4会被加到S
S.push(edge[k]);
low[cur] = min(low[cur], num[v]);
}
k = edge[k].next;
}
if(father < 0)
{
//把根节点看做普通节点了,所以下面最后的特殊判断必需。
if(child > 1) iscut[cur] = 1, add_bcc[cur] = child-1;
else iscut[cur] = 0, add_bcc[cur] = 0;
}
}
void Find_Cut(int l, int r)
{
index = bcc_cnt = yltd = 0;
memset(add_bcc, 0, sizeof add_bcc);
memset(num, 0, sizeof num);
memset(iscut, 0, sizeof iscut);
memset(bccno, 0, sizeof bccno);
memset(low, 0, sizeof low);
for(int i = l; i <= r; ++i)
{
if(!num[i]) tarjan(i, -1), ++yltd;
}
}
void PutAll(int l, int r)
{
for(int i = l; i <= r; ++i)
{
if(iscut[i]) printf("%d是割点,", i);
printf("去掉点%d之后有%d个双连通分量\n", i, add_bcc[i]+yltd);
}
}
void PutBcc()
{
printf("有%d个BCC\n", bcc_cnt);
for(int i = 1; i <= bcc_cnt; ++i)
{
printf("BCC%d有%d个点: ", i, bcc[i].size());
for(int j = 0; j < bcc[i].size(); ++j) printf("%d ", bcc[i][j]);
printf("\n");
}
}
int main()
{
while(~scanf("%d %d", &n, &m))
{
init();
input();
Find_Cut(1, n);
PutAll(1, n);
PutBcc();
}
return 0;
}
/*
测试样例:
8 11
1 2
2 3
3 4
2 4
2 5
2 6
5 6
1 7
1 8
7 8
2 8
*/ 双连通分量的求法就比较朴素了。
Code:
#include
using namespace std;
const int maxn = 110;
const int maxm = 10010;
struct node
{
int u, v, next;
}edge[maxm];
int n, m; //点数,边数
int head[maxn], no;
int index; //时间戳
int num[maxn], low[maxn];//时间戳和能回到的最早时间戳
int iscutedge[maxm];//是否为割边,存邻接表的索引
inline void init()
{
no = 0;
memset(head, -1, sizeof head);
}
inline void add(int u, int v)
{
edge[no].u = u; edge[no].v = v;
edge[no].next = head[u]; head[u] = no++;
edge[no].u = v; edge[no].v = u;
edge[no].next = head[v]; head[v] = no++;
}
inline void input()
{
int u, v;
for(int i = 1; i <= m; ++i)
{
scanf("%d %d", &u, &v);
add(u, v);
}
}
void tarjan(int cur, int father)
{
num[cur] = low[cur] = ++index;
int k = head[cur];
while(k != -1)
{
int v = edge[k].v;
if(!num[v])
{
tarjan(v, cur);
low[cur] = min(low[cur], low[v]);
if(low[v] > num[cur])
{
//把割边的两个方向的边都标记
iscutedge[k] = iscutedge[k^1] = 1;
}
}
else if(edge[k].v != father)
{
low[cur] = min(low[cur], num[v]);
}
k = edge[k].next;
}
}
//找出割边标记上
void Find_CutEdge(int l, int r)
{
index = 0;
memset(iscutedge, 0, sizeof iscutedge);
memset(num, 0, sizeof num);
memset(low, 0, sizeof low);
for(int i = l; i <= r; ++i)
{
if(!num[i]) tarjan(i, -1);
}
}
int dfs(int cur)
{
num[cur] = 1;
int flag = 0; //判断是否存在边双联通分量,以免多输出换行
for(int k = head[cur]; k != -1; k = edge[k].next)
{
if(iscutedge[k]) continue;
flag = 1;
iscutedge[k] = iscutedge[k^1] = 1;
printf("(%d, %d) ", cur, edge[k].v);
if(!num[edge[k].v]) dfs(edge[k].v);
}
return flag;
}
//dfs输出就能得到相应的双连通分量
void PutBccEdge(int l, int r)
{
memset(num, 0, sizeof num);
printf("双连通分量的边有:\n");
for(int i = l; i <= r; i++)
if(!num[i])
{
if(dfs(i)) cout << endl;
}
}
int main()
{
while(~scanf("%d %d", &n, &m))
{
init();
input();
Find_CutEdge(1, n);
PutBccEdge(1, n);
}
return 0;
}
/*
测试样例:
8 10
1 2
2 3
3 4
2 4
2 5
2 6
5 6
1 7
1 8
7 8
*/ 找完割边然后进行DFS输出所有边双连通分量所包含的边~(例题:poj 3352)。
Code2(正确模板方法):
#include
using namespace std;
const int maxn = 25005;
const int maxm = 1e5+5;
struct node {
int u, v, next;
} edge[maxm];
int no, head[maxn];
int idx, dfn[maxn], low[maxn];
int top, S[maxn];
int bcc_cnt, cut;
int bccno[maxn];
vector bcc[maxn];
int n, m;
void init()
{
no = 0;
memset(head, -1, sizeof head);
}
void add(int u, int v)
{
edge[no].u = u; edge[no].v = v;
edge[no].next = head[u]; head[u] = no++;
}
void tarjan(int u, int fa)
{
dfn[u] = low[u] = ++idx;
S[++top] = u;
for(int k = head[u]; k+1; k = edge[k].next)
{
int v = edge[k].v;
if(!dfn[v])
{
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > dfn[u])
{
++cut; //割边+1
}
}
else if(v != fa)
{
low[u] = min(low[u], dfn[v]);
}
}
if(dfn[u] == low[u])
{
++bcc_cnt; //边双连通分量+1
do
{
bcc[bcc_cnt].push_back(S[top]);
bccno[S[top]] = bcc_cnt;
--top;
}
while(S[top+1] != u);
}
}
void work()
{
memset(dfn, 0, sizeof dfn);
memset(bccno, 0, sizeof bccno);
idx = top = bcc_cnt = cut = 0;
for(int i = 1; i <= n; ++i)
if(!dfn[i]) tarjan(i, i);
for(int i = 1; i <= bcc_cnt; ++i)
{
cout << i << ": ";
for(int j = 0; j < bcc[i].size(); ++j)
cout << bcc[i][j] << " ";
cout << endl;
}
}
int main()
{
init();
cin >> n >> m;
for(int i = 1; i <= m; ++i)
{
int u, v;
cin >> u >> v;
add(u, v); add(v, u);
}
work();
return 0;
}
/*
input:
6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6
output:
1: 5 6 4
2: 2 3 1
*/ 之前的错误理解:tarjan之后图中low值相同的两个点必定在同一个边双连通分量中。
上述说法是错误的,上述代码做法是正确的。
继续加油~