图论中的概念(2)——度、正则与悬挂
1.结点的出度: (out-degree)
有向图中以结点v为起点的有向边的条数称为结点v的出度。记为 。
2.结点的进度: (入度(in-degree))
有向图中以结点v为终点的有向边的条数称为结点v的进度。记为 。
3.结点的度: (degree)
图中与结点v关联的边的条数称为结点v的度。记为deg(v)。
4.奇结点: (odd vertex)
度数为奇数的结点称为奇结点。
5.偶结点: (even vertex)
度数为偶数的结点称为偶结点。
6.图G的最小度: (minimal degree)
图G中各结点度数的最小者。记为 d(G) 。
7.图G的最大度: (maximum degree)
图G中各结点度数的最大者。记为 D(G) 。
正则图: (regular graph)
若图G中各结点的度数都相等,则称图G 是正则图。 显然,这时 d(G)=D(G) 。
(29)k-正则的: (k- regular)
若图G中各结点的度数都相等,且为k ,则称图G 是
k-正则的,或k度正则的。 显然,这时 d(G)=D(G)= k 。
(30)悬挂点: (hang vertex)
度数为1的结点称为悬挂点。
(31)悬挂边: (hang edge)
与悬挂点关联的边称为悬挂边。
例1
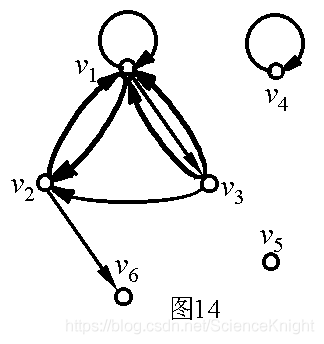
有向图14中,其中:
=3, =4 ,deg(v1)=7 ;
=2, =2 ,deg(v2)=4 ;
=3, =1 ,deg(v3)=4 ;
=1, =1 ,deg(v4)=2 ;
=0, =0 ,deg(v5)=0 ;
=0, =1 ,deg(v6)=1 ;
奇结点: v1, v6 ;
偶结点:v2, v3, v4 , v5 ;
悬挂点: v6 ;
悬挂边: (v2, v6) 。
有如下结论:
(1)所有结点的度数之和等于边数的二倍;
7+4+4+2+0+1=2´9
(2)所有结点的进度之和等于出度之和等于边数;
4+2+1+1+0+1=3+2+3+1+0+0=9
(3)所有奇结点的度数之和是偶数;
7+1=8 。
例2
在下面的无向图中,其中:
deg(v1)=5,deg(v2)=3,deg(v3)=3,
deg(v4)=2,deg(v5)=0,deg(v6)=1 ;
奇结点:v1, v2, v3, v6 ;
偶结点:v4 , v5 ;
悬挂点: v6 ;
悬挂边: (v2, v6) 。
并且有如下结论:
(1)所有结点的度数之和等于边数的二倍;
5+3+3+2+0+1=2´7
(2)所有奇结点的度数之和是偶数;
5+3+3+1=12 。
定理1. 设 G = (V, E) 是 (n,m) 图,则
(1)无向图G中,所有结点的度之和等于边数的二倍;即
dev(vi)=2m 。
(2)有向图G中,所有结点的进度之和等于出度之和等于边数;即
。
[证].(采用‘数钱法’)
(1)因为无向图G中的每条无向边都与两个结点相关联,所以每条边都能给G中结点的度数贡献2,因而G中所有的m条边能给G中结点的度数总计贡献2m,故G中所有结点的度数之和为2m,即
dev(vi)=2m 。
(2)对于有向图G ,每条有向边都与一个终点和一个
起点相关联,因此每条有向边都能给G中结点的进度贡献1,给出度贡献1,因而G中所有的m条边能给G中结点的进度总计贡献m,给出度总计贡献m,故G中所有结点的进度之和等于出度之和等于边数m ,即
。
定理2.任何图中所有奇结点的度数之和是偶数。
[证].设图中共有n个结点;其中奇结点的个数为n1 ,并且不妨设奇结点为u1, u2,¼, un1 ;偶结点的个数为n2 (当然有n1+ n2=n) ,并且不妨设偶结点为w1, w2, ¼, wn2 , 其对应的度数为2k1, 2k2, ¼, 2kn2 ;于是有奇结点度数之和
=2m-(2k1+2k2+ ¼ +2kn2) (定理1)
=2[m-(k1+k2+ ¼ +kn2)]
是偶数。
推论1.(握手引理) 在一次集会上和奇数个人握过手的人的数目是偶数。
[证]. 用结点表示人,用边表示两人相互握过手,从而便可得到一个图。这个图表达了参加集会的人之间彼此握手打招呼的情况。于是直接应用定理2,即可知推论的结论成立。