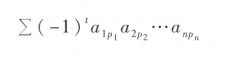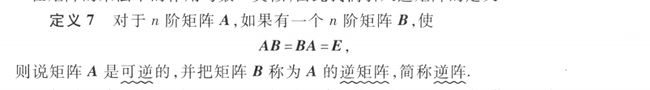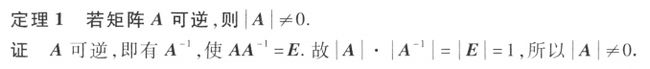- 【树一线性代数】005入门
Owlet_woodBird
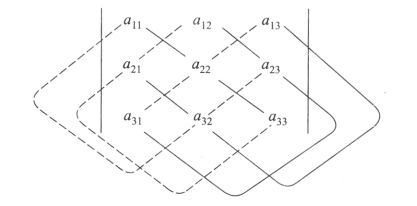
算法
Index本文稍后补全,推荐阅读:https://blog.csdn.net/weixin_60702024/article/details/141874376分析实现总结本文稍后补全,推荐阅读:https://blog.csdn.net/weixin_60702024/article/details/141874376已知非空二叉树T的结点值均为正整数,采用顺序存储方式保存,数据结构定义如下:t
- 如何有效的学习AI大模型?
Python程序员罗宾
学习人工智能语言模型自然语言处理架构
学习AI大模型是一个系统性的过程,涉及到多个学科的知识。以下是一些建议,帮助你更有效地学习AI大模型:基础知识储备:数学基础:学习线性代数、概率论、统计学和微积分等,这些是理解机器学习算法的数学基础。编程技能:掌握至少一种编程语言,如Python,因为大多数AI模型都是用Python实现的。理论学习:机器学习基础:了解监督学习、非监督学习、强化学习等基本概念。深度学习:学习神经网络的基本结构,如卷
- 每日小计划
小糊涂神
活到老学到老到,学习永无止境,我坚持每天学习,我的学习计划如下:1.每天学习五个英语单词,和正在学习英语的儿子共同进步,方便辅导他。2.学习一节统计学或者一节线性代数课程,在此基础上进一步学习数据的处理软件。3.每天微信步数达到1万步,每天饭后过一下二人世界,不到沟通感情,而且还能强身健体!4.学习两节税务师课件,中级会计师已经通过,距离考高级还有几年,空档期考取税务师,充实自己的专业知识。5.坚
- 深度学习算法,该如何深入,举例说明
liyy614
深度学习
深度学习算法的深入学习可以从理论和实践两个方面进行。理论上,深入理解深度学习需要掌握数学基础(如线性代数、概率论、微积分)、机器学习基础和深度学习框架原理。实践上,可以通过实现和优化深度学习模型来提升技能。理论深入数学基础线性代数:理解向量、矩阵、特征值和特征向量等,对于理解神经网络的权重和偏置矩阵至关重要。概率论:用于理解模型的不确定性,如Dropout等正则化技术。微积分:理解梯度下降等优化算
- 非理工科院校怎么打好数学建模比赛 | 南川笔记
南川笔记
Proposition1非理工科院校最好不要打数学建模比赛。虽说“一次建模,终身受益”,但毕竟数学建模既要数学理论的支撑(不仅仅是大学里的微积分、线性代数和概率论与统计,更多的是基于微积分的常偏微分方程、基于线性代数的运筹学和基于概率论与统计的统计分析内容),还要编程的支撑(不是常规的C语言或者Java程序,也不是这几年很火的Python编程,而是基于数值运算的Matlab和基于统计的R),这在一
- 【鼠鼠学AI代码合集#5】线性代数
鼠鼠龙年发大财
鼠鼠学AI系列代码合集人工智能线性代数机器学习
在前面的例子中,我们已经讨论了标量的概念,并展示了如何使用代码对标量进行基本的算术运算。接下来,我将进一步说明该过程,并解释每一步的实现。标量(Scalar)的基本操作标量是只有一个元素的数值。它可以是整数、浮点数等。通过下面的Python代码,我们可以很容易地进行标量的加法、乘法、除法和指数运算。代码实现:importtorch#定义两个标量x=torch.tensor(3.0)#标量x,值为3
- 数学基础 -- 线性代数正交多项式之勒让德多项式展开推导
sz66cm
线性代数决策树算法
勒让德多项式展开的详细过程勒让德多项式是一类在区间[−1,1][-1,1][−1,1]上正交的多项式,可以用来逼近函数。我们可以将一个函数表示为勒让德多项式的线性组合。以下是如何推导勒让德多项式展开系数ana_nan的详细过程。1.勒让德展开的基本假设给定一个函数f(x)f(x)f(x),我们希望将它表示为勒让德多项式的线性组合:f(x)=∑n=0∞anPn(x),f(x)=\sum_{n=0}^
- 线性代数基础
wq_151
mathematic线性代数
Base对于矩阵A,对齐做SVD分解,即UΣV=svd(A)U\SigmaV=svd(A)UΣV=svd(A).其中U为AATAA^TAAT的特征向量,V为ATAA^TAATA的特征向量。Σ\SigmaΣ的对角元素为降序排序的特征值。显然,U、V矩阵中的列向量相互正交,所以也可以视V为svd分解给出了A的列向量空间的正交基,其中最大奇异值(或特征值)对应的特征向量捕捉了数据变化的最大方向。求满足A
- 2022考研数学李永乐复习全书pdf版-基础篇(数一二三通用)
面包资料屋
考研数学
2022考研数学李永乐复习全书pdf版-基础篇(数一二三通用):https://pan.baidu.com/s/1tK9cPPG5Q-xhasqb051ymQ提取码:1111本书是专门为准备参加硕士研究生入学考试提前复习的大二大三学生、在职考研人士及基础薄弱的考生编写。本书以初等数学水平为起点,阐述了考研数学要求的基本知识构架。希望本书能够帮助考生在短时间内厘清考研数学(包括高等数学、线性代数、概
- 线性代数|机器学习-P33卷积神经网络ImageNet和卷积规则
取个名字真难呐
算法机器学习矩阵人工智能线性代数
文章目录1.ImageNet2.卷积计算2.1两个多项式卷积2.2函数卷积2.3循环卷积3.周期循环矩阵和非周期循环矩阵4.循环卷积特征值4.1卷积计算的分解4.2运算量4.3二维卷积公式5.KroneckerProduct1.ImageNetImageNet的论文paper链接如下:详细请直接阅读相关论文即可通过网盘分享的文件:imagenet_cvpr09.pdf链接:https://pan.
- Python的图形化界面编程
iteye_20668
Pythonpython
2017.2.14好久没有写代码了,感觉过一个年弄的什么也没有干成,好像看了下c++,突然发现现在来看C++,要简单了好多,并且指针也没有那么难了,然后就是看了下机器学习,感觉有点小难,现在发现好多都涉及到高数,概率论和线性代数的知识,想想当初把这些学的是一塌糊涂。然后上次和胡杨大大聊天的时候,他说好多东西都是在实践中去学习的。好了,继续我的Python吧,Python的图形化界面编程。impor
- matlab初等变换函数,线性代数实践及 MATLAB 入门(2005年10月)
weixin_39861905
matlab初等变换函数
出版时间:2005-10-1作者:陈怀琛,龚杰民编著出版社:电子工业出版社程序集名为dsk05,课件名bk05课件内容简介本书是根据“用软件工具提高线性代数教学”的指导思想,参照美国1992—1997国家科学基金项目ATLAST的思路,编写成的线性代数补充教材,其目的是补充我国现有教材的的缺陷。它分为两篇,第一篇介绍线性代数所用的软件工具MATLAB语言,它可以作为教材,也可以作为手册使用;第二篇
- matlab线性代数电子书,实用大众线性代数 MATLAB版_13652907.pdf
三金乐了
matlab线性代数电子书
【作者】陈怀琛著【形态项】156【出版项】西安:西安电子科技大学出版社,2014.08【ISBN号】978-7-5606-3462-3【中图法分类号】O151.2【原书定价】20.00【主题词】线性代数-计算机辅助设计-MATLAB软件【参考文献格式】陈怀琛著.实用大众线性代数MATLAB版.西安:西安电子科技大学出版社,2014.08.内容提要:传统的线性代数源于数学家,教理论不教应用。工科需要
- 数学基础 -- 线性代数之格拉姆-施密特正交化
sz66cm
线性代数机器学习人工智能
格拉姆-施密特正交化格拉姆-施密特正交化(Gram-SchmidtOrthogonalization)是一种将一组线性无关的向量转换为一组两两正交向量的算法。通过该过程,我们能够从原始向量组中构造正交基,并且可以选择归一化使得向量组成为标准正交基。算法步骤假设我们有一组线性无关的向量{v1,v2,…,vn}\{v_1,v_2,\dots,v_n\}{v1,v2,…,vn},其目标是将这些向量正交化
- Matlab初等数学与线性代数
崔渭阳
matlabmatlab线性代数数据结构
初等数学算术运算基本算术加法+添加数字,追加字符串sum数组元素总和cumsum累积和movsum移动总和A=1:5;B=cumsum(A)B=1×51361015减法-减法diff差分和近似导数乘法.*乘法*矩阵乘法prod数组元素的乘积cumprod累积乘积pagemtimes按页矩阵乘法(自R2020b起)tensorprodTensorproductsbetweentwotensors(自
- 数学基础 -- 线性代数之矩阵的迹
sz66cm
线性代数机器学习决策树
矩阵的迹什么是矩阵的迹?矩阵的迹(TraceofaMatrix)是线性代数中的一个基本概念,定义为一个方阵主对角线上元素的总和。矩阵的迹在许多数学和物理应用中都起着重要作用,例如在矩阵分析、量子力学、统计学和系统理论中。矩阵迹的定义对于一个n×nn\timesnn×n的方阵AAA:A=(a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮an1an2⋯ann)A=\begin{pmatrix}a_{1
- 线性代数 第五讲:线性方程组_齐次线性方程组_非齐次线性方程组_公共解同解方程组_详解
小徐要考研
线性代数线性代数线性方程组机器学习
线性方程组文章目录线性方程组1.齐次线性方程组的求解1.1核心要义1.2基础解系与线性无关的解向量的个数1.3计算使用举例2.非齐次线性方程的求解2.1非齐次线性方程解的判定2.2非齐次线性方程解的结构2.3计算使用举例3.公共解与同解3.1两个方程组的公共解3.2同解方程组4.方程组的应用5.重难点题型总结5.1抽象齐次线性方程组的求解5.1含有系数的非齐次线性方程组的求解及有条件求全部解问题5
- Day04-线性代数-特征值和特征向量(DataWhale)
liying_tt
数学基础线性代数
七、特征值和特征向量AAA是n阶方阵,数λ\lambdaλ,若存在非零列向量α⃗\vec{\alpha}α,使得Aα⃗=λα⃗A\vec{\alpha}=\lambda\vec{\alpha}Aα=λα,则λ\lambdaλ是特征值,α⃗\vec{\alpha}α是对应于λ\lambdaλ的特征向量λ\lambdaλ可以为0α⃗\vec{\alpha}α不能为0⃗\vec{0}0,且为列向量Aα⃗
- 人工智能中的线性代数与矩阵论学习秘诀之著名教材
audyxiao001
人工智能怎么学人工智能线性代数矩阵学习方法
线性代数是大学数学中非常核心的基础课程,教材繁多,国内外有许多经典的教材。国内比较有名且使用较为广泛的线性代数中文教材见书籍8。书籍8线性代数中文教材推荐:(a)简明线性代数(丘维声);(b)线性代数(居于马);(c)线性代数(李尚志);(d)线性代数(李炯生等);(e)线性代数五讲(龚昇);(f)线性代数的几何意义(任广千等)北京大学的丘维声教授编写的《简明线性代数》[17]是北京市高等教育精品
- 数学基础 -- 线性代数之矩阵正定性
sz66cm
线性代数矩阵
线性代数中的正定性正定性在线性代数中主要用于描述矩阵的特性,尤其是在二次型与优化问题中有重要应用。正定矩阵的定义对于一个n×nn\timesnn×n的对称矩阵AAA,其正定性可以通过以下条件来判断:正定矩阵:如果对于任意非零向量x∈Rnx\in\mathbb{R}^nx∈Rn,二次型xTAxx^TAxxTAx都是正的,即:xTAx>0∀x∈Rn,x≠0x^TAx>0\quad\forallx\in
- 线性代数笔记【二次型】
内 鬼
微电子专业笔记线性代数矩阵
二次型n元二次型:关于n个变量x1,x2,⋯ ,xnx_1,x_2,\cdots,x_nx1,x2,⋯,xn的二次齐次函数KaTeXparseerror:Nosuchenvironment:align*atposition8:\begin{̲a̲l̲i̲g̲n̲*̲}̲f(x_1,x_2,\cdo…系数全为实数的二次型叫做实二次型,除此之外还有复二次型和复二次型矩阵,但在这里不讨论标准二次型:只含
- MIT线性代数
模拟IC和AI的Learner
线性代数线性代数机器学习算法
P5置换矩阵置换矩阵是行重新排列的单位矩阵。置换矩阵用P表示,性质:n阶置换矩阵共有n!个P6零空间某个矩阵的零空间中的向量经过该矩阵的变换后都落在0向量,
- MIT线性代数
模拟IC和AI的Learner
线性代数
本文链接的原创作者为浊酒南街https://blog.csdn.net/weixin_43597208第1讲MIT_线性代数笔记:第01讲行图像和列图像-CSDN博客第2讲MIT_线性代数笔记:第02讲矩阵消元_矩阵firstpivot-CSDN博客第3讲MIT_线性代数笔记:第03讲矩阵的乘法和逆矩阵_矩阵行乘列和列乘行-CSDN博客第4讲MIT_线性代数笔记:第04讲矩阵的LU分解-CSDN博
- 从零开始学数据分析之——《线性代数》第六章 二次型
doubleyue1314
线性代数数据分析数据挖掘算法
6.1二次型与对称矩阵6.1.1二次型及其矩阵定义:n个变量的二次齐次函数称为的一个n元二次型,简称为二次型二次型转换为矩阵表达式:1)平方项的系数直接作为主对角元素2)交叉项的系数除以2放两个对称的相应位置上二次型的矩阵一定是对称的二次型的标准形对应的矩阵是一个对角形矩阵,其秩为主对角线上非零元的个数矩阵表达式写为二次型:1)主对角线元素直接作为平方项的系数2)取主线右上角元素乘以2作为交叉项系
- 线性代数学习笔记8-4:正定矩阵、二次型的几何意义、配方法与消元法的联系、最小二乘法与半正定矩阵A^T A
Insomnia_X
线性代数学习笔记线性代数矩阵学习
正定矩阵Positivedefinitematrice之前说过,正定矩阵是一类特殊的对称矩阵:正定矩阵满足对称矩阵的特性(特征值为实数并且拥有一套正交特征向量、正/负主元的数目等于正/负特征值的数目)另外,正定矩阵还具有更好的性质(所有特征值都为正实数、所有主元都为正实数、左上角的所有任意k阶(10(x≠0)\mathbf{x}^{T}\boldsymbol{A}\mathbf{x}>0\quad
- LU分解算法(串行、并行)
清榎
高性能计算并行程序高性能计算数值分析
一、串行LU分解算法(详细见MIT线性代数)1.LU分解矩阵分解LU分解分解形式L(下三角矩阵)、U(上三角矩阵)目的提高计算效率前提(1)矩阵A为方阵;(2)矩阵可逆(满秩矩阵);(3)消元过程中没有0主元出现,也就是消元过程中不能出现行交换的初等变换LU分解其实就是将线性方程组:Ax=bAx=bAx=b分解为:LUx=bLUx=bLUx=b这样一来就会有:{Ly=bUx=y\begin{cas
- 线性代数 --- LU分解(Gauss消元法的矩阵表示)
松下J27
LinearAlgebra线性代数矩阵LU分解高斯消元矩阵运行gaussianLU
Gauss消元法等价于把系数矩阵A分解成两个三角矩阵L和U的乘法首先,LU分解实际上就是用矩阵的形式来记录的高斯消元的过程。其中,对矩阵A进行高斯消元后的结果为矩阵U,是LU分解后的两个三角矩阵中其中之一。U是一个上三角矩阵,U就是上三角矩阵uppertriangle的首字母的大写。高斯消元的每一步都能用基本消元矩阵E来表示。而所有的E都可以收录在一个矩阵当中,我这里叫他Z矩阵。Z矩阵就是集所有基
- Python NumPy 库详解
寒秋丶
Pythonpythonnumpy开发语言测试开发数据分析数据挖掘软件测试
大家好,在当今数据驱动的世界中,处理大规模数据、进行复杂数值计算是科学研究、工程设计以及数据分析的关键任务之一。在Python生态系统中,NumPy(NumericalPython)库是一款备受推崇的工具,它为我们提供了高效的数组操作、数学函数以及线性代数运算等功能,成为了科学计算和数据处理的利器。一、介绍NumPyNumPy(NumericalPython)是Python中一个开源的数值计算库,
- 【机器人工具箱Robotics Toolbox开发笔记(一)】Matlab机器人工具箱简介
DRobot
机器人工具箱RoboticsToolbox开发笔记机器人笔记matlab
MATLAB是一款被广泛应用于科学计算和工程领域的专业软件。它的全称为MatrixLaboratory(矩阵实验室),因为其最基本的数据类型就是矢量与矩阵,所以在处理数学和科学问题时非常方便,可用于线性代数计算、图形和动态仿真的高级技术计算语言和交互式环境以及解决机器人学的相关问题。MATLAB的RoboticsToolbox(简称RTB)是一款在MATLAB环境下进行机器人建模、仿真和控制的工具
- 线性代数——特征值与特征向量的性质
lwh 98+106
线性代数算法机器学习
(1)设A为方阵,则A与ATA^{T}AT有相同的特征值。此处用到了两个关键性质,一:单位阵的转置为其本身,二:转置并不改变行列式的值。(2):设n阶方阵A=(aija_{ij}aij)的n个特征值为λ1\lambda_{1}λ1,λ2\lambda_{2}λ2,…λn\lambda_{n}λn,则λ1+λ2+λ3+...λn=a11+a22+a33+...+ann\lambda_{1}+\lam
- 矩阵求逆(JAVA)初等行变换
qiuwanchi
矩阵求逆(JAVA)
package gaodai.matrix;
import gaodai.determinant.DeterminantCalculation;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
/**
* 矩阵求逆(初等行变换)
* @author 邱万迟
*
- JDK timer
antlove
javajdkschedulecodetimer
1.java.util.Timer.schedule(TimerTask task, long delay):多长时间(毫秒)后执行任务
2.java.util.Timer.schedule(TimerTask task, Date time):设定某个时间执行任务
3.java.util.Timer.schedule(TimerTask task, long delay,longperiod
- JVM调优总结 -Xms -Xmx -Xmn -Xss
coder_xpf
jvm应用服务器
堆大小设置JVM 中最大堆大小有三方面限制:相关操作系统的数据模型(32-bt还是64-bit)限制;系统的可用虚拟内存限制;系统的可用物理内存限制。32位系统下,一般限制在1.5G~2G;64为操作系统对内存无限制。我在Windows Server 2003 系统,3.5G物理内存,JDK5.0下测试,最大可设置为1478m。
典型设置:
java -Xmx
- JDBC连接数据库
Array_06
jdbc
package Util;
import java.sql.Connection;
import java.sql.DriverManager;
import java.sql.ResultSet;
import java.sql.SQLException;
import java.sql.Statement;
public class JDBCUtil {
//完
- Unsupported major.minor version 51.0(jdk版本错误)
oloz
java
java.lang.UnsupportedClassVersionError: cn/support/cache/CacheType : Unsupported major.minor version 51.0 (unable to load class cn.support.cache.CacheType)
at org.apache.catalina.loader.WebappClassL
- 用多个线程处理1个List集合
362217990
多线程threadlist集合
昨天发了一个提问,启动5个线程将一个List中的内容,然后将5个线程的内容拼接起来,由于时间比较急迫,自己就写了一个Demo,希望对菜鸟有参考意义。。
import java.util.ArrayList;
import java.util.List;
import java.util.concurrent.CountDownLatch;
public c
- JSP简单访问数据库
香水浓
sqlmysqljsp
学习使用javaBean,代码很烂,仅为留个脚印
public class DBHelper {
private String driverName;
private String url;
private String user;
private String password;
private Connection connection;
privat
- Flex4中使用组件添加柱状图、饼状图等图表
AdyZhang
Flex
1.添加一个最简单的柱状图
? 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
<?xml version=
"1.0"&n
- Android 5.0 - ProgressBar 进度条无法展示到按钮的前面
aijuans
android
在低于SDK < 21 的版本中,ProgressBar 可以展示到按钮前面,并且为之在按钮的中间,但是切换到android 5.0后进度条ProgressBar 展示顺序变化了,按钮再前面,ProgressBar 在后面了我的xml配置文件如下:
[html]
view plain
copy
<RelativeLa
- 查询汇总的sql
baalwolf
sql
select list.listname, list.createtime,listcount from dream_list as list , (select listid,count(listid) as listcount from dream_list_user group by listid order by count(
- Linux du命令和df命令区别
BigBird2012
linux
1,两者区别
du,disk usage,是通过搜索文件来计算每个文件的大小然后累加,du能看到的文件只是一些当前存在的,没有被删除的。他计算的大小就是当前他认为存在的所有文件大小的累加和。
- AngularJS中的$apply,用还是不用?
bijian1013
JavaScriptAngularJS$apply
在AngularJS开发中,何时应该调用$scope.$apply(),何时不应该调用。下面我们透彻地解释这个问题。
但是首先,让我们把$apply转换成一种简化的形式。
scope.$apply就像一个懒惰的工人。它需要按照命
- [Zookeeper学习笔记十]Zookeeper源代码分析之ClientCnxn数据序列化和反序列化
bit1129
zookeeper
ClientCnxn是Zookeeper客户端和Zookeeper服务器端进行通信和事件通知处理的主要类,它内部包含两个类,1. SendThread 2. EventThread, SendThread负责客户端和服务器端的数据通信,也包括事件信息的传输,EventThread主要在客户端回调注册的Watchers进行通知处理
ClientCnxn构造方法
&
- 【Java命令一】jmap
bit1129
Java命令
jmap命令的用法:
[hadoop@hadoop sbin]$ jmap
Usage:
jmap [option] <pid>
(to connect to running process)
jmap [option] <executable <core>
(to connect to a
- Apache 服务器安全防护及实战
ronin47
此文转自IBM.
Apache 服务简介
Web 服务器也称为 WWW 服务器或 HTTP 服务器 (HTTP Server),它是 Internet 上最常见也是使用最频繁的服务器之一,Web 服务器能够为用户提供网页浏览、论坛访问等等服务。
由于用户在通过 Web 浏览器访问信息资源的过程中,无须再关心一些技术性的细节,而且界面非常友好,因而 Web 在 Internet 上一推出就得到
- unity 3d实例化位置出现布置?
brotherlamp
unity教程unityunity资料unity视频unity自学
问:unity 3d实例化位置出现布置?
答:实例化的同时就可以指定被实例化的物体的位置,即 position
Instantiate (original : Object, position : Vector3, rotation : Quaternion) : Object
这样你不需要再用Transform.Position了,
如果你省略了第二个参数(
- 《重构,改善现有代码的设计》第八章 Duplicate Observed Data
bylijinnan
java重构
import java.awt.Color;
import java.awt.Container;
import java.awt.FlowLayout;
import java.awt.Label;
import java.awt.TextField;
import java.awt.event.FocusAdapter;
import java.awt.event.FocusE
- struts2更改struts.xml配置目录
chiangfai
struts.xml
struts2默认是读取classes目录下的配置文件,要更改配置文件目录,比如放在WEB-INF下,路径应该写成../struts.xml(非/WEB-INF/struts.xml)
web.xml文件修改如下:
<filter>
<filter-name>struts2</filter-name>
<filter-class&g
- redis做缓存时的一点优化
chenchao051
redishadooppipeline
最近集群上有个job,其中需要短时间内频繁访问缓存,大概7亿多次。我这边的缓存是使用redis来做的,问题就来了。
首先,redis中存的是普通kv,没有考虑使用hash等解结构,那么以为着这个job需要访问7亿多次redis,导致效率低,且出现很多redi
- mysql导出数据不输出标题行
daizj
mysql数据导出去掉第一行去掉标题
当想使用数据库中的某些数据,想将其导入到文件中,而想去掉第一行的标题是可以加上-N参数
如通过下面命令导出数据:
mysql -uuserName -ppasswd -hhost -Pport -Ddatabase -e " select * from tableName" > exportResult.txt
结果为:
studentid
- phpexcel导出excel表简单入门示例
dcj3sjt126com
PHPExcelphpexcel
先下载PHPEXCEL类文件,放在class目录下面,然后新建一个index.php文件,内容如下
<?php
error_reporting(E_ALL);
ini_set('display_errors', TRUE);
ini_set('display_startup_errors', TRUE);
if (PHP_SAPI == 'cli')
die('
- 爱情格言
dcj3sjt126com
格言
1) I love you not because of who you are, but because of who I am when I am with you. 我爱你,不是因为你是一个怎样的人,而是因为我喜欢与你在一起时的感觉。 2) No man or woman is worth your tears, and the one who is, won‘t
- 转 Activity 详解——Activity文档翻译
e200702084
androidUIsqlite配置管理网络应用
activity 展现在用户面前的经常是全屏窗口,你也可以将 activity 作为浮动窗口来使用(使用设置了 windowIsFloating 的主题),或者嵌入到其他的 activity (使用 ActivityGroup )中。 当用户离开 activity 时你可以在 onPause() 进行相应的操作 。更重要的是,用户做的任何改变都应该在该点上提交 ( 经常提交到 ContentPro
- win7安装MongoDB服务
geeksun
mongodb
1. 下载MongoDB的windows版本:mongodb-win32-x86_64-2008plus-ssl-3.0.4.zip,Linux版本也在这里下载,下载地址: http://www.mongodb.org/downloads
2. 解压MongoDB在D:\server\mongodb, 在D:\server\mongodb下创建d
- Javascript魔法方法:__defineGetter__,__defineSetter__
hongtoushizi
js
转载自: http://www.blackglory.me/javascript-magic-method-definegetter-definesetter/
在javascript的类中,可以用defineGetter和defineSetter_控制成员变量的Get和Set行为
例如,在一个图书类中,我们自动为Book加上书名符号:
function Book(name){
- 错误的日期格式可能导致走nginx proxy cache时不能进行304响应
jinnianshilongnian
cache
昨天在整合某些系统的nginx配置时,出现了当使用nginx cache时无法返回304响应的情况,出问题的响应头: Content-Type:text/html; charset=gb2312 Date:Mon, 05 Jan 2015 01:58:05 GMT Expires:Mon , 05 Jan 15 02:03:00 GMT Last-Modified:Mon, 05
- 数据源架构模式之行数据入口
home198979
PHP架构行数据入口
注:看不懂的请勿踩,此文章非针对java,java爱好者可直接略过。
一、概念
行数据入口(Row Data Gateway):充当数据源中单条记录入口的对象,每行一个实例。
二、简单实现行数据入口
为了方便理解,还是先简单实现:
<?php
/**
* 行数据入口类
*/
class OrderGateway {
/*定义元数
- Linux各个目录的作用及内容
pda158
linux脚本
1)根目录“/” 根目录位于目录结构的最顶层,用斜线(/)表示,类似于
Windows
操作系统的“C:\“,包含Fedora操作系统中所有的目录和文件。 2)/bin /bin 目录又称为二进制目录,包含了那些供系统管理员和普通用户使用的重要
linux命令的二进制映像。该目录存放的内容包括各种可执行文件,还有某些可执行文件的符号连接。常用的命令有:cp、d
- ubuntu12.04上编译openjdk7
ol_beta
HotSpotjvmjdkOpenJDK
获取源码
从openjdk代码仓库获取(比较慢)
安装mercurial Mercurial是一个版本管理工具。 sudo apt-get install mercurial
将以下内容添加到$HOME/.hgrc文件中,如果没有则自己创建一个: [extensions] forest=/home/lichengwu/hgforest-crew/forest.py fe
- 将数据库字段转换成设计文档所需的字段
vipbooks
设计模式工作正则表达式
哈哈,出差这么久终于回来了,回家的感觉真好!
PowerDesigner的物理数据库一出来,设计文档中要改的字段就多得不计其数,如果要把PowerDesigner中的字段一个个Copy到设计文档中,那将会是一件非常痛苦的事情。