智能车竞赛逆透视变换(含编程实现)
在阅读本文之前,应该先阅读朱葛峻的《逆透视变换的一种方法》(下简称《方法》),本文的实现是基于这篇文章的推导的。
本文中提到的方法主要用于智能车竞赛。虽然在智能车有限的视野和像素内,这种方法有时并不是一种很好的选择。
目录
-
- 一、基本理论
- 二、实现原理
- 三、代码实现
一、基本理论
在谈逆透视变换之前,我们先谈一下真实世界和智能车上安装的摄像头所获取的照片的关系。世界坐标系下的点要经历平移变换、旋转变换、缩放变换、投影变换而得到摄像头坐标系下的点。前三种变换都是一一映射的变换,即原坐标下的点唯一对应新坐标下的点。只要知道规则,逆变换就可以完成。
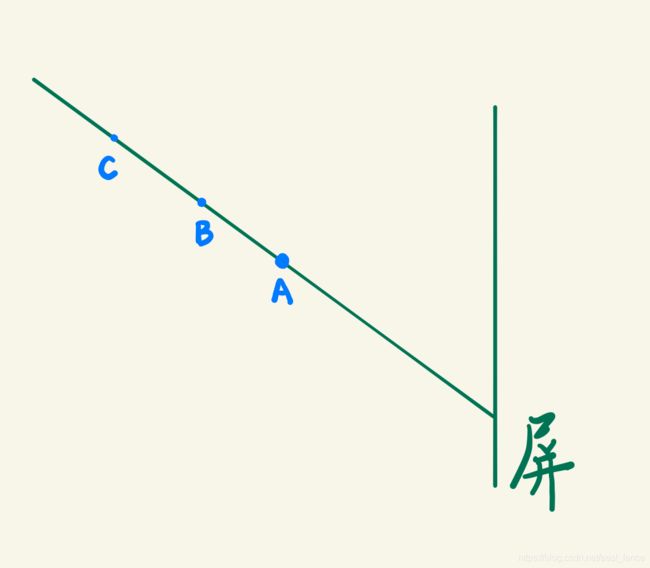
投影变换不是一一映射的变换。如图,B,C两点在以A点为投影点的变换中落到了屏上同一点。B,C因为缺少深度的信息,在逆变换中无法区分。
在智能车的应用场景中,所有点都在地面,即Z=0。就是说,深度信息没有丢失,所以逆透视变换是可以完成的。
如下图,一张矩形的由摄像头获得的照片,在逆透视变换后变换成了倒梯形,而蓝色阴影所表示的道路则通过变换呈现出俯视图的样子。
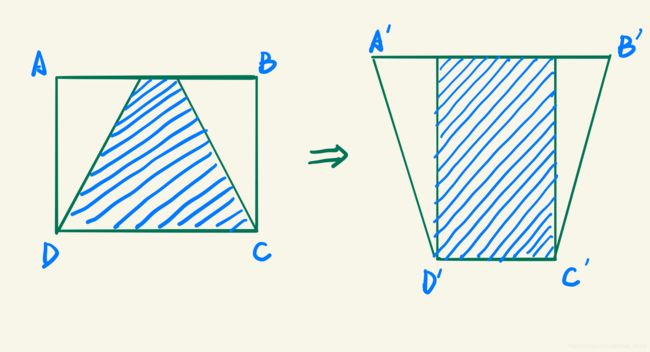
二、实现原理
在下面的推导中,二维平面内的坐标点会用三维的列向量表示。 x , y x,y x,y为摄像头坐标系内点的坐标。 X , Y X,Y X,Y为世界坐标系内点的坐标。
[ x y w ] 与 [ x / w y / w 1 ] \begin{bmatrix}x\\y\\w\end{bmatrix}与\begin{bmatrix}x/w\\y/w\\1\end{bmatrix} ⎣⎡xyw⎦⎤与⎣⎡x/wy/w1⎦⎤表示同一个点。
按照小孔摄像机的数学模型,有
[ x ‾ y ‾ s ‾ ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 ] [ X Y 0 1 ] \begin{bmatrix}\overline{x}\\\overline{y}\\\overline{s}\end{bmatrix}=\begin{bmatrix} f_x&0&c_x\\0&f_y&c_y\\0&0&1\end{bmatrix}\begin{bmatrix} r_{11}&r_{12}&r_{13}&t_1\\ r_{21}&r_{22}&r_{23}&t_2\\ r_{31}&r_{32}&r_{33}&t_3 \end{bmatrix}\begin{bmatrix}X\\ Y\\ 0\\ 1\end{bmatrix} ⎣⎡xys⎦⎤=⎣⎡fx000fy0cxcy1⎦⎤⎣⎡r11r21r31r12r22r32r13r23r33t1t2t3⎦⎤⎣⎢⎢⎡XY01⎦⎥⎥⎤
化简得
[ x ‾ y ‾ s ‾ ] = [ H 11 H 12 H 12 H 21 H 22 H 23 H 31 H 32 1 ] [ X Y 1 ] \begin{bmatrix}\overline{x}\\\overline{y}\\\overline{s}\end{bmatrix}=\begin{bmatrix} H_{11}&H_{12}&H_{12}\\H_{21}&H_{22}&H_{23}\\H_{31}&H_{32}&1\end{bmatrix}\begin{bmatrix}X\\ Y\\ 1\end{bmatrix} ⎣⎡xys⎦⎤=⎣⎡H11H21H31H12H22H32H12H231⎦⎤⎣⎡XY1⎦⎤
令 H = [ H 11 H 12 H 12 H 21 H 22 H 23 H 31 H 32 1 ] H=\begin{bmatrix} H_{11}&H_{12}&H_{12}\\H_{21}&H_{22}&H_{23}\\H_{31}&H_{32}&1\end{bmatrix} H=⎣⎡H11H21H31H12H22H32H12H231⎦⎤, H H H的逆为 H d H_d Hd,
H d = [ H d 11 H d 12 H d 12 H d 21 H d 22 H d 23 H d 31 H d 32 1 ] H_d=\begin{bmatrix} H_{d11}&H_{d12}&H_{d12}\\H_{d21}&H_{d22}&H_{d23}\\H_{d31}&H_{d32}&1\end{bmatrix} Hd=⎣⎡Hd11Hd21Hd31Hd12Hd22Hd32Hd12Hd231⎦⎤
有
[ X ‾ Y ‾ S ‾ ] = [ H d 11 H d 12 H d 12 H d 21 H d 22 H d 23 H d 31 H d 32 1 ] [ x y 1 ] \begin{bmatrix}\overline{X}\\\overline{Y}\\\overline{S}\end{bmatrix}=\begin{bmatrix} H_{d11}&H_{d12}&H_{d12}\\H_{d21}&H_{d22}&H_{d23}\\H_{d31}&H_{d32}&1\end{bmatrix}\begin{bmatrix}x\\ y\\ 1\end{bmatrix} ⎣⎡XYS⎦⎤=⎣⎡Hd11Hd21Hd31Hd12Hd22Hd32Hd12Hd231⎦⎤⎣⎡xy1⎦⎤
于是有了变换公式
X = X ‾ S ‾ = H d 11 x + H d 12 y + H d 13 H d 31 x + H d 32 y + H d 33 X=\frac{\overline{X}}{\overline{S}}=\frac{H_{d11}x+H_{d12}y+H_{d13}}{H_{d31}x+H_{d32}y+H_{d33}} X=SX=Hd31x+Hd32y+Hd33Hd11x+Hd12y+Hd13
Y = Y ‾ S ‾ = H d 21 x + H d 22 y + H d 23 H d 31 x + H d 32 y + H d 33 Y=\frac{\overline{Y}}{\overline{S}}=\frac{H_{d21}x+H_{d22}y+H_{d23}}{H_{d31}x+H_{d32}y+H_{d33}} Y=SY=Hd31x+Hd32y+Hd33Hd21x+Hd22y+Hd23
H H H和 H d H_d Hd的推导,贴出《方法》中的原公式。

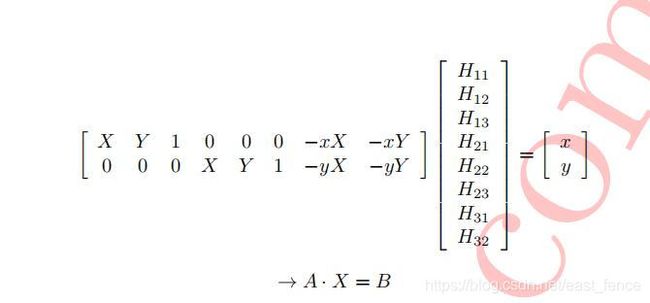
要想方程组有唯一解,需要带入四个点在世界坐标系和摄像头坐标系的坐标。可以参考第一部分中的示意图。
注意在实际操作中, x , y , X , Y x,y,X,Y x,y,X,Y可以直接使用从零开始、从左至右、从上到下增加的像素坐标。还要注意 x , X x,X x,X是纵坐标, y , Y y,Y y,Y是横坐标。
三、代码实现
下面的matlab代码,用来计算 H H H和 H d H_d Hd。
x=[30,30,119,119] % 依次为A、B、D、C在摄像头获取的照片中的的纵坐标
y=[0,187,0,187] % 依次为A、B、D、C在摄像头获取的照片中的的横坐标
X=[4000,4000,5465,5465] % 依次为A、B、D、C在逆透视变换后的照片中的的纵坐标
Y=[3000,5720,4132,4580] % 依次为A、B、D、C在逆透视变换后的照片中的的纵坐标
A = [X(1),Y(1),1,0,0,0,-x(1)*X(1),-x(1)*Y(1);
0,0,0,X(1),Y(1),1,-y(1)*X(1),-y(1)*Y(1);
X(2),Y(2),1,0,0,0,-x(2)*X(2),-x(2)*Y(2);
0,0,0,X(2),Y(2),1,-y(2)*X(2),-y(2)*Y(2);
X(3),Y(3),1,0,0,0,-x(3)*X(3),-x(3)*Y(3);
0,0,0,X(3),Y(3),1,-y(3)*X(3),-y(3)*Y(3);
X(4),Y(4),1,0,0,0,-x(4)*X(4),-x(4)*Y(4);
0,0,0,X(4),Y(4),1,-y(4)*X(4),-y(4)*Y(4)];
B = [x(1);y(1);x(2);y(2);x(3);y(3);x(4);y(4)];
H=A\B; % 求解H11到H18
H=H' % 把列向量改成行向量
H=[H,1] % 获得完整的H的行向量
H11 =H(1);H12 =H(2); H13 =H(3); H21 =H(4); H22 =H(5); H23 =H(6); H31 =H(7); H32 =H(8); H33=H(9);
H=[H11,H12,H13;H21,H22,H23;H31,H32,H33] % 获得完整的H的矩阵
Hd=inv(H) % 获得Hd矩阵
fprintf("[[%f, %f, %f], [%f, %f, %f], [%f, %f, %f]]",Hd(1,1),Hd(1,2),Hd(1,3),Hd(2,1),Hd(2,2),Hd(2,3),Hd(3,1),Hd(3,2),Hd(3,3)); % 把Hd矩阵以符合python列表的形式输出
def process(self,img):
img = np.array(img)
height = 10000 # 高度限制
width = 8000 # 宽度限制
output = np.full((height, width), 0, dtype=np.int)
Hd=[[1075.629450, 0.000000, -19146.217384], [814.163487, 47.718786, -14582.905023], [0.186940, 0.000000, -2.327535]]
# 这里把刚从matlab那里得到的
for x in range(img.shape[0]):
for y in range(img.shape[1]):
X = round((x * Hd[0][0] + y * Hd[0][1] + Hd[0][2]) / (x * Hd[2][0] + y * Hd[2][1] + Hd[2][2]))
Y = round((x * Hd[1][0] + y * Hd[1][1] + Hd[1][2]) / (x * Hd[2][0] + y * Hd[2][1] + Hd[2][2]))
# 注意由于python的索引从0开始计数,这里的索引和公式里略有差别
if X>=height:
X = height-1
if X<0:
X=0
if Y >= width:
Y = width-1
if Y<0:
Y=0
output[X,Y]=img[x,y]
return output
