Projective Geometric Algebra, PGA 射影几何代数. SIGGRAPH 2019 Course Notes. Chpt. 4
Projective Geometric Algebra 射影几何代数
参考并概括自 Geometric Algebra for Computer Graphics, Siggraph 2019 Course Notes, Charles G. Gunn 。
注:非翻译。跳过了第1, 2, 3的导入章节。本文图片均引用自参考文献。
Projective Geometric Algebra,射影几何代数,下面简称PGA,是欧式空间中处理几何关系的一套代数工具。几何的代数工具对于在现代工程学、CAD、VR、3D游戏、动画等各个相关领域非常重要。一般比较熟悉也是应用十分广泛的,是向量、线性代数、解析几何(Vector and Linear Algebra and Analytic Geometric, 简称VLAAG)的一套框架。而PGA是另一套现代方法,与传统的VLAAG方法有所不同,从另一个角度,另一个观点来求解欧式空间中的几何问题。
Chpt. 4 Immersive introduction to geometric algebra
几何代数的基本哲学就是:几何的运算都是数的运算(Geometric primitives behave like numbers)。在PGA中,基本形(geometric primitives. 点、直线、平面)等,由**外代数(exterior algebra)**中不同阶(grade)的向量表示,例如3D空间中:
- scalar: 0-vector
- plane: 1-vector
- lines : 2-vector
- point: 3-vector
每一阶的都构成一个向量代数空间(运算为加法和乘法)。几何代数的元素被称作多重向量(multivector),是k-vector的“和”。一个multivector M M M的k阶部分,记作 ⟨ M ⟩ k \langle M \rangle_k ⟨M⟩k。几何图元之间的关系通过**几何积(geometric product)**来表达。
下面举一些用PGA解决常见几何问题的形式化的例子,感受PGA方法的框架的运用。
Example 1. 3D空间中的点直线
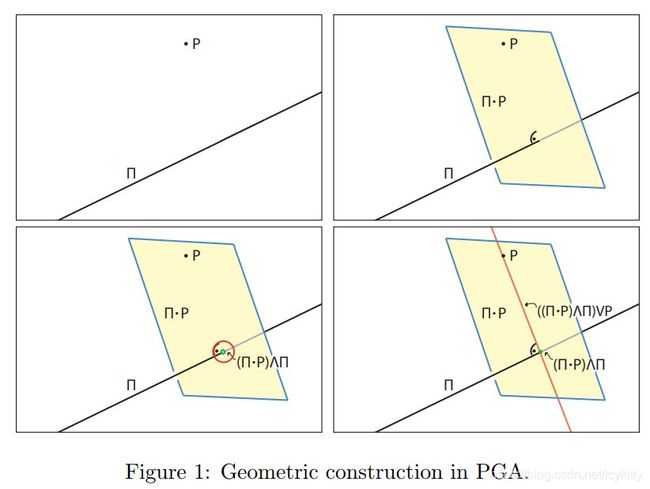
目标任务:对三维欧式空间 E 3 E^3 E3中给定的一个点 P P P,一个不经过该点的直线 Π \Pi Π。找到唯一的直线 Σ \Sigma Σ经过 P P P点并和直线 Π \Pi Π正交。
一个直线 Π \Pi Π(2-vector),和一个点 P P P(3-vector),通过几何积 Π P \Pi P ΠP,包含了两个部分,一个1-vector,一个3-vector
Π P = ⟨ Π P ⟩ 1 + ⟨ Π P ⟩ 3 \Pi P=\langle \Pi P\rangle_1+\langle \Pi P \rangle_3 ΠP=⟨ΠP⟩1+⟨ΠP⟩3
- ⟨ Π P ⟩ 1 \langle \Pi P\rangle_1 ⟨ΠP⟩1 是垂直于直线 Π \Pi Π过点 P P P的平面,记作 Π ⋅ P \Pi \cdot P Π⋅P
- ⟨ Π P ⟩ 3 \langle \Pi P\rangle_3 ⟨ΠP⟩3 是平面的法线方向。在这个例子中用不到。
如Fig. 1中所示,我们想求的直线 Σ \Sigma Σ可以这样得到:
- Π ⋅ P \Pi \cdot P Π⋅P是垂直于直线 Π \Pi Π过点 P P P的平面
- 点 ( Π ⋅ P ) ∧ Π (\Pi\cdot P)\wedge \Pi (Π⋅P)∧Π是平面 Π ⋅ P \Pi \cdot P Π⋅P与直线 Π \Pi Π的交点
- 直线 Σ : = ( ( Π ⋅ P ) ∧ Π ) ∨ P \Sigma :=((\Pi\cdot P)\wedge\Pi)\lor P Σ:=((Π⋅P)∧Π)∨P,是交点到 P P P的直线。其中, ∧ \wedge ∧ ∨ \lor ∨是外代数中的运算概念。后面的章节将会详细介绍。
Example 2. 一个3D万花筒(Kaleidoscope)
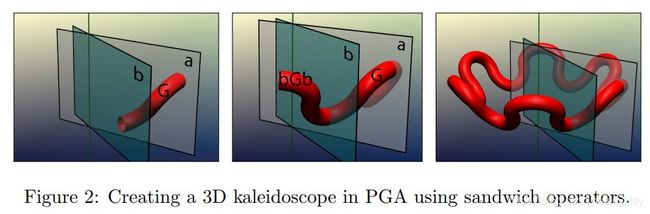
目标任务:一个 k-Kaleidoscope 是 E 3 E^3 E3中一对镜子平面 a , b \bold{a},\bold{b} a,b,两平面之间夹角为 Π / k \Pi/k Π/k。给一个几何体 G G G,通过镜像复制,生成一个 G G G在这个“万花筒”中看到的形状。
在PGA中, a \bold{a} a是一个1-vector。可以normalize使得 a 2 = 1 \bold{a}^2=1 a2=1。在PGA中,一个物体对几何的反射,通过**"sandwich"运算** a G a \bold{aGa} aGa实现,其中 G \bold{G} G可以是任意的几何元。 a 2 = 1 \bold{a}^2=1 a2=1的作用是保证几何体经过sandwich形状相同。
在Fig. 2 第二幅图中,是 b G b \bold{bGb} bGb和 a G a \bold{aGa} aGa的结果。第三幅图中,是 G \bold{G} G对 a , b \bold{a,b} a,b任何可能的所有反射的结果(e.g. b a G a b \bold{baGab} baGab)。例如,若镜子平面的夹角是 Π / 6 \Pi/6 Π/6,则这个万花筒反射复制了 12 12 12个几何体 G \bold{G} G。(在这里, ( a b ) 6 = ( b a ) 6 = 1 \bold{(ab)}^6=\bold{(ba)}^6=1 (ab)6=(ba)6=1)。
Example 3. 一个3D中连续螺旋的动作

目标任务:表示一个3D的连续螺旋动作(screw motion)
E 3 E^3 E3中一般的物体姿态方向不变的变换是螺旋动作,即围绕一个特定直线(轴)旋转,同时沿平行于这个直线的方向平移。平移距离和旋转弧度的比,叫做螺距(pitch)。只有旋转的运动的螺距是0,只有平移的运动的螺距是 ∞ \infty ∞。
在Example 2. 中,我们已经看到了包含旋转的操作,它通过在两个有夹角的平面之间反射实现。(i.e., b ( a G a ) b \bold{b(aGa)b} b(aGa)b,就是旋转两倍反射平面夹角的结果,在上面的例子中是 π / 3 \pi/3 π/3)。
下面我们用不同但有些类似的方法来得到绕特定轴的旋转。在 E 3 E^3 E3中,一个过点 P P P,以 V V V为方向的直线通过 Ω : = P ∨ V \Omega:=P\lor V Ω:=P∨V得到(Fig. 3中的黄线)。可以通过normalize使得 Ω 2 = − 1 \Omega^2=-1 Ω2=−1。为了得到围绕 Ω \Omega Ω旋转 α \alpha α的转动,定义motor e t Ω e^{t\Omega} etΩ. 感觉类似于以复数为指数,因为 Ω 2 = − 1 \Omega^2=-1 Ω2=−1。利用前面的sandwich运算,我们就得到 e t Ω G e − t Ω e^{t\Omega}Ge^{-t\Omega} etΩGe−tΩ,就能够实现 G G G围绕 Ω \Omega Ω连续旋转的结果。若 t = 0 t=0 t=0,则保持不变。 t = α / 2 t=\alpha/2 t=α/2时,表示旋转弧度 α \alpha α。对四元数熟悉的读者应该能注意到它与四元数表示旋转的相似之处,这并不是巧合。在后面的章节中会介绍。
为了得到一个沿 Ω \Omega Ω的平移变换,我们用一个不同的直线:通过polarity运算: Ω ⊥ \Omega^\perp Ω⊥。 Ω ⊥ \Omega^\perp Ω⊥是 Ω \Omega Ω的正交补,且长度为无穷。它由所有 Ω \Omega Ω垂直的方向组成。如果 Ω \Omega Ω看做是一个竖直的轴,则 Ω ⊥ \Omega^\perp Ω⊥是水平直线。在PGA中,正交补是通过乘上一个特殊的 4-vector得到的,单位**伪标量(pseudoscalar,**是几何代数最强大也有趣的工具之一) I : Ω ⊥ : = Ω I \bold{I:\Omega^\perp:=\Omega I} I:Ω⊥:=ΩI。一个连续的平移是通过一个对平移量 e t Ω ⊥ e^{t\Omega^\perp} etΩ⊥做sandwich运算得到的。
将上面的旋转、平移结合起来,对于螺距为 p ∈ R p\in \R p∈R的螺旋运动,可以表示为
e t ( Ω + p Ω ⊥ ) = e t Ω e t p Ω ⊥ e^{t(\Omega+p\Omega^\perp)}=e^{t\Omega} e^{tp\Omega^\perp} et(Ω+pΩ⊥)=etΩetpΩ⊥
用它来对 G \bold{G} G作sandwich运算。
在接下来的章节中,将会介绍PGA的数学基础。
参考文献
[1] Charles G. Gunn. Course notes Geometric Algebra for Computer Graphics SIGGRAPH 2019.
水平有限,笔记概括可能有不好的地方。如有错误请指正,如有疑惑可参考上述资料。