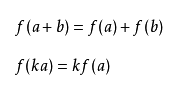线性函数、非线性函数与线性回归的区别
线性函数、非线性函数与线性回归的区别
-
- 线性规划和非线性规划的区别
-
- （一）目标或约束条件不同
- （二）最优解范围不同
- 线性函数与非线性函数
-
- 线性变换：
- 线性关系
- 应用编辑
- 线性规划中的 0-1规划问题
在数学建模中，数学规划包含线性规划和非线性规划,两者与机器学习中的线性回归有很大区别。
线性规划和非线性规划的区别
（一）目标或约束条件不同
（1）线性规划目标和约束均为线性函数
（2）非线性规划目标或约束中存在非线性函数
（二）最优解范围不同
线性规划的最优解如果存在，只能存在可行域的边界上找到（一般还是在顶点处）；
非线性规划的最优解可能存在于可行域的任意一点达到。
线性函数与非线性函数
1、在数学里，线性函数是指那些线性的函数，但也常用作一次函数的别称，尽管一次函数不一定是线性的（那些不经过原点的）。
2、非线性函数即函数图像不是一条直线的函数。非线性函数包括指数函数、幂函数、对数函数、多项式函数、基本初等函数以及他们组成的复合函数。
线性变换：
在线性代数里，线性函数是一个线性映射。
设 V 和 W 是在相同域 K 上的向量空间。函数 f : V → W 被称为是线性映射，如果对于 V 中任何两个向量 a和 b与 K 中任何标量 k，满足下列两个条件：
即其维持向量加法与标量乘法。 [1]
如果 W 等同域 K ，也称 f 是 V上的一个线性函数。
例如，若我们用坐标向量 (Coordinate vector) 来表示 x 与 f(x) ，那么线性函数可以表达为
f(x)=M*x；其中，M是矩阵。
线性关系
两个变量之间存在一次函数关系，就称它们之间存在线性关系。
更通俗一点讲，如果把这两个变量分别作为点的横坐标与纵坐标，其图象是平面上的一条直线，则这两个变量之间的关系就是线性关系。
注：正比例关系是线性关系中的特例，反比例关系不是线性关系。
在高等数学里，线性函数是一个线性映射，是在两个向量空间之间，维持向量加法与标量乘法的映射。
例如，假若，我们用坐标向量(coordinate vector来表示 x x x 与 f ( x ) f(x) f(x)。那么，线性函数可以表达为
其中， M M M 是矩阵。
应用编辑
仿射变换是指一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。
一个对 x ⃗ \vec{x} x向量 平移 b ⃗ \vec{b} b，与旋转放大缩小 A A A的仿射映射为
上式在齐次坐标上，等价于下面的式子
在分形的研究里，收缩平移仿射映射可以制造制具有自相似性的分形。
一个在两个仿射空间之间的仿射变换，是在向量上呈现线性之坐标点的变换（即为空间中点与点之间的向量）。以符号表示的话， f ′ {f}' f′使得 φ \varphi φ ，决定任一对点的线性变换： P , Q ∈ A P,Q\in A P,Q∈A
仿射变换表示
如上所示，仿射变换为两函数的复合：平移及线性映射。普通向量代数用矩阵乘法呈现线性映射, 用向量加法表示平移。正式言之，于有限维度之例中，假如该线性映射被表示为一矩阵“A”，平移被表示为向量 b ⃗ \vec{b} b ，一仿射映射 f f f可被表示为
线性规划中的 0-1规划问题
0–1规划是指：未知量的取值范围只能是0,1的规划问题，通常是线性规划
主要解决问题：多个人做一项工作，只能由一人做的规划问题
例如：问应指派哪个人去承担哪件工作，才能使总的花费时间最少？
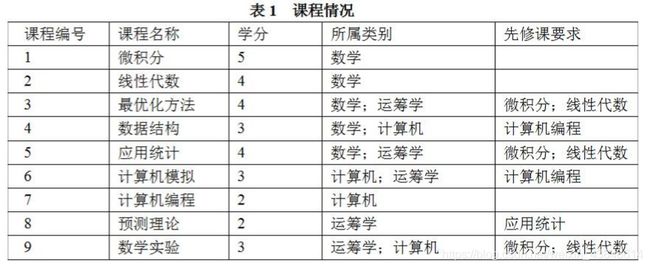
选修课策略问题 某学校规定，运筹学专业的学生毕业时必须至少学习过两门数学课、三门运 筹学课和两门计算机课。这些课程的编号、名称、学分、所属类别和先修课要求 如表1所示。
问题：
(1) 毕业时学生最少可以学习这些课程中哪些课程。
(2)如果某个学生既希望选修课程的数量少，又希望所获得的 学分多，他可以选修哪些课程？
模型的建立
约束条件包括两个方面：
第一方面是课程数量的约束：
第二方面是先修课程的关系约束：
总的0-1规划模型为：
model:
sets: item/1..9/:x;
endsets
min=@sum(item(i):x(i));!课程最少; x(1)+x(2)+x(3)+x(4)+x(5)>=2; x(3)+x(5)+x(6)+x(8)+x(9)>=3;
x(4)+x(6)+x(7)+x(9)>=2;
x(3)<=x(1); x(3)<=x(2);
x(4)<=x(7); x(5)<=x(1);
x(5)<=x(2); x(6)<=x(7);
x(8)<=x(5); x(9)<=x(1);
x(9)<=x(2);
@for(item(i):@bin(x(i)));
end
使用Lingo软件求解即可
关于机器学习中线性回归更多解释