伸展树
伸展树(Splay Tree)是一种二叉排序树,它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。它的优势在于不需要记录用于平衡树的冗余信息。在伸展树上的一般操作都基于伸展操作。
为什么需要伸展树(Splay Tree)
各种查找树存在不足。比如:对于一个有n个节点的平衡树,虽然最坏情况下每次查找的时间复杂度不会超过O(logn),但是如果访问模式不均匀,平衡树的效率就会受到影响。此外,它们还需要额外的空间来存储平衡信息。
这些查找树的设计目标都是减少最坏情况下单次操作时间,但是查找树的典型应用经常需要执行一系列的查找操作,此时更关心的性能指标是所有这些操作总共需要多少时间。对于此类应用,更好的目标就是降低操作的摊平时间,此处的摊平时间是指在一系列最坏情况的操作序列中单次操作的平均时间。获得摊平效率的一种方法就是使用“自调整”的数据结构。
和平衡的或是其它对结构有明确限制的数据结构比起来,自调整数据结构有以下几个优点:
1、从摊平角度而言,它们忽略常量因子,因此绝对不会比有明确限制的数据结构差。而且由于它们可以根据使用情况进行调整,于是在使用模式不均匀的情况下更加有效。
2、由于无需存储平衡或者其它的限制信息,它们所需的空间更小。
当然,自调整结构也有潜在的缺点:
1、它们需要更多的局部调整,尤其是在查找期间。(那些有明确限制的数据结构仅需在更新期间进行调整,查找期间则不用)
2、一系列查找操作中的某一个可能会耗时较长,这在实时应用程序中可能是个不足之处。
什么是伸展树(Splay Tree)
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。splay tree应运而生。splay tree是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
两种重构方法:
1、单旋:在查找完位于节点x中的条目i之后,旋转链接x和其父节点的边。(除非x就是树根)
2、搬移至树根:在查找完位于节点x中的条目i之后,旋转链接x和其父节点的边,然后重复这个操作直至x成为树根。
旋转示意图:

注:
x为p(x)的左孩子,交换x和p(x)的位置,称为:右旋p(x)
x为p(x)的右孩子,交换x和p(x)的位置,称为:左旋p(x)
伸展树的自底向上伸展(bottom-up splay)
splay tree的重构方法和搬移至树根的方法相似,它也会沿着查找路径做自底向上的旋转,将被查找条目移至树根。但不同的是,它的旋转是成对进行的,顺序取决于查找路径的结构。为了在节点x处对树进行splay操作,我们需要重复下面的步骤,直至x成为树根为止:
注:图中 R-当前节点 Q-父亲节点 P-祖父节点
1、第一种情况:如果x的父节点p(x)是树根,则旋转连接x和p(x)的边。(这种情况是最后一步)

2、第二种情况:如果p(x)不是树根,而且x和p(x)本身都是左孩子或者都是右孩子,则先旋转连接p(x)和x的祖父节点g(x)的边,然后再旋转连接x和p(x)的边。

3、第三种情况:如果p(x)不是树根,而且x是左孩子,p(x)是右孩子,或者相反,则先旋转连接x和p(x)的边,再旋转连接x和新的p(x)的边。

在节点x处进行splay操作的时间是和查找x所需的时间成比例的。splay操作不单是把x搬移到了树根,而且还把查找路径上的每个节点的深度都大致减掉了一半。
伪代码:
假设在当前伸展树中的X节点处进行伸展, X的父亲节点为P(X) (如果X的父亲节点存在),
X的祖父节点为 G(X)(如果 X的祖父节点存在)。
FUNC bottom-up-splay
DO
IF X 是 P(X)的左孩子节点 THEN
IF G(X)为空 THEN
右旋 P(X)
ELSEIF P(X)是 G(X)的左孩子节点 THEN
右旋 G(X)
右旋 P(X)
ELSE
右旋 P(X)
左旋 P(X)(注意:经过上一次右旋后此处的 P(X)和上一个 P(X)不一样)
ENDIF
ELSE X是 P(X)的右孩子节点 THEN
IF G(X)为空 THEN
左旋 P(X)
ELSEIF P(X)是 G(X)的右孩子节点 THEN
左旋 G(X)
左旋 P(X)
ELSE
左旋 P(X)
右旋 P(X) (注意:经过上一次左旋后此处的 P(X)和上一个 P(X)不一样)
ENDIF
ENDIF
WHILE P(X)不为空
ENDFUNC

伸展树的自顶向下伸展(top-down splay)
自顶向下伸展操作将伸展树分为三部分:
左树:包含所有已经知道比待查节点 X小的节点。
右树:包含所有已经知道比待查节点 X大的节点。
中树:包含所有其它节点。
在中树自根向下进行节点查找(每次向下比较两个节点),根据查找情况将中树中的节
点移动(此处的移动是指将节点和中树的连接断开,而将节点连接到左或右树的适当位置。)到左树或右树(如有必要则会先对中树进行旋转再进行节点移动)。
初始状态时,左树和右树都为空,而中树为整个原伸展树。随着查找的进行,左树和右
树会因节点的逐渐移入变大,中树会因节点的逐渐移出变小。最后查找结束(找到或遇到空
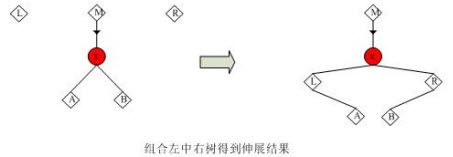
节点)时组合左中右树并是伸展树自顶向下伸展方法的最终结果。
有四种情况:
1,孩子即为要查找的点,只需要一次连接操作即可.

2,孙子为要查找的点,且左右孩子一致.需要首先旋转父亲和祖父节点,然后连接操作.

3,孙子为要查找的点,且左右孩子不一致.需要两次连接操作.
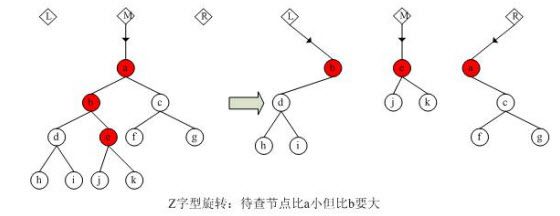
4,合并
伪代码:
其中的 L、R 分别表示左树和右树且初始值为空,M 为中树且初值为原伸展树;X为待查节点,T 为 M 的根节点。
FUNC top-down-splay
DO
IF X 小于 T THEN
IF X 等于 T 的左孩子 THEN
右连接
ELSEIF X 小于 T 的左孩子 THEN
右旋
右连接
ELSE X大于 T 的左孩子 THEN
右连接
左连接
ENDIF
ELSE X大于 T THEN
IF X 等于 T 的右孩子 THEN
左连接
ELSEIF X 大于 T 的右孩子 THEN
左旋
左连接
ELSE X小于 T 的右孩子 THEN
左连接
右连接
ENDIF
ENDIF
WHILE 找到 X或遇到空节点
组合左中右树
ENDFUNC
伸展树(Splay Tree)支持的操作
具体操作包括:
1、access(i,t):如果i在树t中,则返回指向它的指针,否则返回空指针。为了实现 access(i,t),可以从树t的根部向下查找i。如果查找操作遇到了一个含有i的节点x,就在x处进行splay操作,并返回指向x的指针,访问结束。如果遇到了空指针,表示i不在树中,此时就在最后一个非空节点处进行splay操作,然后返回空指针。如果树是空的,将忽略掉splay操作。
2、insert(i,t):将条目i插入树t中(假设其尚不存在)。为了实现insert(i,t),首先执行split(i,t),然后把t换成一个由新的包含有i的根节点组成的树,这个根节点的左右子树分别是split返回的树t1和t2。
3、delete(i,t):从树t中删除条目i(假设其已经存在)。为了实现delete(i,t),首先执行access(i,t),然后把t换成其左子树和右子树join之后的新树。
4、join(t1,t2):将树t1和t2合并成一棵树,其中包含之前两棵树的所有条目,并返回合并之后的树。这个操作假设t1中的所有条目都小于t2 中的条目,操作完成之后会销毁t1和t2。为了实现join(t1,t2),首先访问t1中最大的条目i。访问结束之后,t1的根节点中包含的就是i,它的右孩子显然为空。于是把t2作为这个根节点的右子树并返回完成之后的新树即可实现join操作。
5、split(i,t):构建并返回两棵树t1和t2,其中t1包含t中所有小于等于i的条目,t2包含t中所有大于i的条目。操作完成之后销毁t。为了实现split(i,t),首先执行access(i,t),然后根据新根节点中的值是大于还是小于等于i来切断这个根节点的左链接或右链接,并返回形成的两棵树。
为什么需要伸展树(Splay Tree)
各种查找树存在不足。比如:对于一个有n个节点的平衡树,虽然最坏情况下每次查找的时间复杂度不会超过O(logn),但是如果访问模式不均匀,平衡树的效率就会受到影响。此外,它们还需要额外的空间来存储平衡信息。
这些查找树的设计目标都是减少最坏情况下单次操作时间,但是查找树的典型应用经常需要执行一系列的查找操作,此时更关心的性能指标是所有这些操作总共需要多少时间。对于此类应用,更好的目标就是降低操作的摊平时间,此处的摊平时间是指在一系列最坏情况的操作序列中单次操作的平均时间。获得摊平效率的一种方法就是使用“自调整”的数据结构。
和平衡的或是其它对结构有明确限制的数据结构比起来,自调整数据结构有以下几个优点:
1、从摊平角度而言,它们忽略常量因子,因此绝对不会比有明确限制的数据结构差。而且由于它们可以根据使用情况进行调整,于是在使用模式不均匀的情况下更加有效。
2、由于无需存储平衡或者其它的限制信息,它们所需的空间更小。
3、它们的查找和更新算法概念简单,易于实现。
【注】从平摊的角度而言
当然,自调整结构也有潜在的缺点:
1、它们需要更多的局部调整,尤其是在查找期间。(那些有明确限制的数据结构仅需在更新期间进行调整,查找期间则不用)
2、一系列查找操作中的某一个可能会耗时较长,这在实时应用程序中可能是个不足之处。
什么是伸展树(Splay Tree)
假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法,在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。splay tree应运而生。splay tree是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
两种重构方法:
1、单旋:在查找完位于节点x中的条目i之后,旋转链接x和其父节点的边。(除非x就是树根)
2、搬移至树根:在查找完位于节点x中的条目i之后,旋转链接x和其父节点的边,然后重复这个操作直至x成为树根。
旋转示意图:

注:
x为p(x)的左孩子,交换x和p(x)的位置,称为:右旋p(x)
x为p(x)的右孩子,交换x和p(x)的位置,称为:左旋p(x)
伸展树的自底向上伸展(bottom-up splay)
splay tree的重构方法和搬移至树根的方法相似,它也会沿着查找路径做自底向上的旋转,将被查找条目移至树根。但不同的是,它的旋转是成对进行的,顺序取决于查找路径的结构。为了在节点x处对树进行splay操作,我们需要重复下面的步骤,直至x成为树根为止:
注:图中 R-当前节点 Q-父亲节点 P-祖父节点
1、第一种情况:如果x的父节点p(x)是树根,则旋转连接x和p(x)的边。(这种情况是最后一步)

2、第二种情况:如果p(x)不是树根,而且x和p(x)本身都是左孩子或者都是右孩子,则先旋转连接p(x)和x的祖父节点g(x)的边,然后再旋转连接x和p(x)的边。

3、第三种情况:如果p(x)不是树根,而且x是左孩子,p(x)是右孩子,或者相反,则先旋转连接x和p(x)的边,再旋转连接x和新的p(x)的边。

在节点x处进行splay操作的时间是和查找x所需的时间成比例的。splay操作不单是把x搬移到了树根,而且还把查找路径上的每个节点的深度都大致减掉了一半。
伪代码:
假设在当前伸展树中的X节点处进行伸展, X的父亲节点为P(X) (如果X的父亲节点存在),
X的祖父节点为 G(X)(如果 X的祖父节点存在)。
FUNC bottom-up-splay
DO
IF X 是 P(X)的左孩子节点 THEN
IF G(X)为空 THEN
右旋 P(X)
ELSEIF P(X)是 G(X)的左孩子节点 THEN
右旋 G(X)
右旋 P(X)
ELSE
右旋 P(X)
左旋 P(X)(注意:经过上一次右旋后此处的 P(X)和上一个 P(X)不一样)
ENDIF
ELSE X是 P(X)的右孩子节点 THEN
IF G(X)为空 THEN
左旋 P(X)
ELSEIF P(X)是 G(X)的右孩子节点 THEN
左旋 G(X)
左旋 P(X)
ELSE
左旋 P(X)
右旋 P(X) (注意:经过上一次左旋后此处的 P(X)和上一个 P(X)不一样)
ENDIF
ENDIF
WHILE P(X)不为空
ENDFUNC

伸展树的自顶向下伸展(top-down splay)
自顶向下伸展操作将伸展树分为三部分:
左树:包含所有已经知道比待查节点 X小的节点。
右树:包含所有已经知道比待查节点 X大的节点。
中树:包含所有其它节点。
在中树自根向下进行节点查找(每次向下比较两个节点),根据查找情况将中树中的节
点移动(此处的移动是指将节点和中树的连接断开,而将节点连接到左或右树的适当位置。)到左树或右树(如有必要则会先对中树进行旋转再进行节点移动)。
初始状态时,左树和右树都为空,而中树为整个原伸展树。随着查找的进行,左树和右
树会因节点的逐渐移入变大,中树会因节点的逐渐移出变小。最后查找结束(找到或遇到空
节点)时组合左中右树并是伸展树自顶向下伸展方法的最终结果。
有四种情况:
1,孩子即为要查找的点,只需要一次连接操作即可.

2,孙子为要查找的点,且左右孩子一致.需要首先旋转父亲和祖父节点,然后连接操作.

3,孙子为要查找的点,且左右孩子不一致.需要两次连接操作.

4,合并

伪代码:
其中的 L、R 分别表示左树和右树且初始值为空,M 为中树且初值为原伸展树;X为待查节点,T 为 M 的根节点。
FUNC top-down-splay
DO
IF X 小于 T THEN
IF X 等于 T 的左孩子 THEN
右连接
ELSEIF X 小于 T 的左孩子 THEN
右旋
右连接
ELSE X大于 T 的左孩子 THEN
右连接
左连接
ENDIF
ELSE X大于 T THEN
IF X 等于 T 的右孩子 THEN
左连接
ELSEIF X 大于 T 的右孩子 THEN
左旋
左连接
ELSE X小于 T 的右孩子 THEN
左连接
右连接
ENDIF
ENDIF
WHILE 找到 X或遇到空节点
组合左中右树
ENDFUNC
伸展树(Splay Tree)支持的操作
具体操作包括:
1、access(i,t):如果i在树t中,则返回指向它的指针,否则返回空指针。为了实现 access(i,t),可以从树t的根部向下查找i。如果查找操作遇到了一个含有i的节点x,就在x处进行splay操作,并返回指向x的指针,访问结束。如果遇到了空指针,表示i不在树中,此时就在最后一个非空节点处进行splay操作,然后返回空指针。如果树是空的,将忽略掉splay操作。
2、insert(i,t):将条目i插入树t中(假设其尚不存在)。为了实现insert(i,t),首先执行split(i,t),然后把t换成一个由新的包含有i的根节点组成的树,这个根节点的左右子树分别是split返回的树t1和t2。
3、delete(i,t):从树t中删除条目i(假设其已经存在)。为了实现delete(i,t),首先执行access(i,t),然后把t换成其左子树和右子树join之后的新树。
4、join(t1,t2):将树t1和t2合并成一棵树,其中包含之前两棵树的所有条目,并返回合并之后的树。这个操作假设t1中的所有条目都小于t2 中的条目,操作完成之后会销毁t1和t2。为了实现join(t1,t2),首先访问t1中最大的条目i。访问结束之后,t1的根节点中包含的就是i,它的右孩子显然为空。于是把t2作为这个根节点的右子树并返回完成之后的新树即可实现join操作。
5、split(i,t):构建并返回两棵树t1和t2,其中t1包含t中所有小于等于i的条目,t2包含t中所有大于i的条目。操作完成之后销毁t。为了实现split(i,t),首先执行access(i,t),然后根据新根节点中的值是大于还是小于等于i来切断这个根节点的左链接或右链接,并返回形成的两棵树。