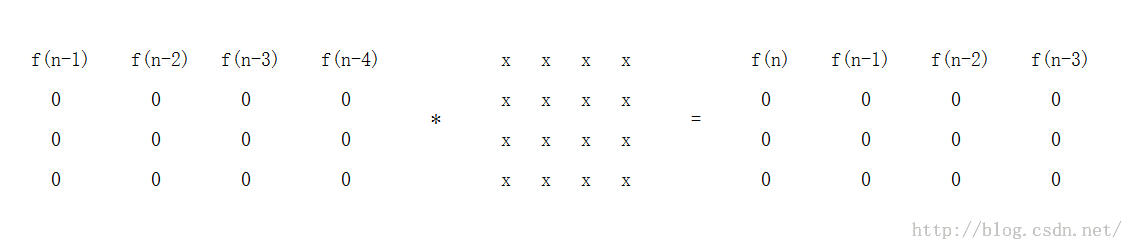HDOJ Queuing 2604【求矩阵+矩阵快速幂】

Queuing

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3528    Accepted Submission(s): 1590

Problem Description

Queues and Priority Queues are data structures which are known to most computer scientists. The Queue occurs often in our daily life. There are many people lined up at the lunch time. 

  Now we define that ‘f’ is short for female and ‘m’ is short for male. If the queue’s length is L, then there are 2 ^L numbers of queues. For example, if L = 2, then they are ff, mm, fm, mf . If there exists a subqueue as fmf or fff, we call it O-queue else it is a E-queue.
Your task is to calculate the number of E-queues mod M with length L by writing a program.

 

Input

Input a length L (0 <= L <= 10  ⁶) and M.

 

Output

Output K mod M(1 <= M <= 30) where K is the number of E-queues with length L.

 

Sample Input

   
   
   
   

    
    
    
    3 8
4 7
4 8
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    6
2
1
   
   
   
   

 

Author

WhereIsHeroFrom

 

Source

HDU 1st “Vegetable-Birds Cup” Programming Open Contest

 

Recommend

lcy   |   We have carefully selected several similar problems for you:   1588  1757  2606  2603  3117 

 

题意：给你一个长度为L的由m和f两种字母组成的字符串，定义存在fmf以及fff子串的都是不符合要求的串，问长度为L的符合要求的串有多少个？

解题思路：

此题如果直接利用递推关系，处理不好会超内存的。

首先找出递推关系式，先给出递推关系式：( L )=( L - 1 ) + ( L - 3 ) + ( L - 4 ); 可以先尝试推导一下，推不出来再看下面的解释。

考虑当L=n时的情况，有两种情况：

①.如果最后一个字符为m ：此时，只要前面长度为n-1的串符合要求，则当前长度为n的串必然符合要求。

②.如果最后一个字符为f：此时，无法确定，因为可能存在不符合要求的串，继续分情况讨论

          (1).最后倒数二个字符为f，仍然可能存在不符合要求的串，继续分情况讨论

                      1.倒数第三个字符为f,因为存在fff，所以该种情况必然不符合要求，舍去

                      2.倒数第三个字符为m，仍然有可能不符合要求，再分

                                   a.最后第四个字符为f，存在fmf，所以该种情况必然不符合要求，舍去

                                   b.最后第四个字符为m,只要前面长度为n-4的串符合要求，则当前长度为n的串必然也符合要求

           (2).最后第二个字符为m，存在可能不符合要求的情况，分

                      1.最后第三个字符为f，存在fmf，此时必然不符合要求舍去

                      2.最后第三个字符为m，只要前面长度为n-3的串的情况符合要求，则当前长度为n的串必然符合要求。

所以讲符合要求的情况相加就得到：( L )=( L - 1 ) + ( L - 3 ) + ( L - 4 ); 

前面已经讲过如果只是用普通递归方法会超内存，所以这里要考虑优化。

怎么优化？先看下面的矩阵相乘的结果：

x矩阵是多少会得到后面的矩阵？我们只需考虑后面矩阵的第一行，因为其他元素为0.

第1行第1列的元素我们需要得到f ( n )，因为f(n)=f(n-1)+f(n-3)+f(n-4); 所以我们必须保留f(n-1)，f(n-3)，f(n-4) 所以与之相乘的数必须为1.

所以第1列元素可以确定，为1 0 1 1，注意，是第一列而不是第一行。

根据第一行第二列元素，我们可以确定x矩阵第二列元素：1 0 0 0.

根据第一行第三列元素，我们可以确定x矩阵第三列元素：0 1 0 0.

根据第一行第四列元素，我们可以确定x矩阵第四列元素：0 0 1 0.

所以x矩阵已经确定，所以我们可以得到下面的矩阵乘式：

所以，反复乘以x矩阵就可以得到想要的f(n);

所以可以先求出x矩阵的L-4(不是L)次方，到这就转化为了矩阵快速幂问题。然后在用  f(4)   f(3)  f(2)   f(1)   乘以求次方后的矩阵的第一列元素  ，相加就得到f(n)=res[0][0]*f[4]+res[1][0]*f[3]+res[2][0]*f[2]+res[3[0]*f[1]。

讲解到此结束~欢迎指出错误~。

AC代码：

#include <stdio.h>
#include <string.h>
#include <algorithm>
#define maxn 5
using namespace std;

int mat[maxn][maxn];
int res[maxn][maxn];
int f[10];

void Matmul(int x[maxn][maxn],int y[maxn][maxn],int Mod)
{
	int t[maxn][maxn]={0};
	for(int i=0;i<4;i++)
		for(int k=0;k<4;k++)
			if(x[i][k])
				for(int j=0;j<4;j++)
				t[i][j]=(t[i][j]+x[i][k]*y[k][j]%Mod)%Mod;
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
		x[i][j]=t[i][j];
}

void Matrix(int t[maxn][maxn],int m,int Mod)
{
	for(int i=0;i<4;i++)
		for(int j=0;j<4;j++)
		res[i][j]=(i==j);
	while(m){
		if(m&1)Matmul(res,t,Mod);
		Matmul(t,t,Mod);
		m>>=1;
	}
}

int main()
{
	int L,M;
	while(scanf("%d%d",&L,&M)!=EOF){
		memset(f,0,sizeof(f));
		f[1]=2;f[2]=4;
	    f[3]=6;f[4]=9;
		int T[maxn][maxn]={0};
		T[0][0]=T[2][0]=T[3][0]=1;
		T[0][1]=T[1][2]=T[2][3]=1;
		if(L==1){
			printf("%d\n",2%M);
			continue;
		}
		if(L==2){
			printf("%d\n",4%M);
			continue;
		}
		if(L==3){
			printf("%d\n",6%M);
			continue;
		}
		if(L==4){
			printf("%d\n",9%M);
			continue;
		}
		Matrix(T,L-4,M);
		int ans=0;
		for(int i=0;i<4;i++){
			ans=(ans+res[i][0]*f[4-i])%M;
		}
		printf("%d\n",ans);
	}
	return 0;
}