莫比乌斯反演的学习（HDU1695）
前两天学习了一下之前一直觉得高大上并且想学的内容——莫比乌斯反演。不过学任何东西都是一样，学会了发现也就这样，虽然只是皮毛。OK，废话不多说，进入正题，今天我用杭电的1695这道题再来温习一下莫比乌斯反演。
HDU1695的题目大意是这样的，给你 a , b , c , d , k 五个值 （题目说明了 你可以认为 a=c=1） x 属于 [1,b] ，y属于[1,d] 让你求有多少对这样的 （x,y）满足gcd（x,y）==k。给你的时间是 3000 MS。 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000
这道题我刚开始看的时候想到的是容斥定理， 由于以前没用容斥写过题，但久闻莫比乌斯反演大名，干脆就学习了一下，如何用莫比乌斯反演来解题。
首先 ，这道题可以进行一部分的简化，因为 gcd（x,y）=k 那么，很显然 gcd（x / k,y / k）是等于 1 的（x,y 除了 k 一定没有其他的公因数）。那么，此时问题就可以转化为： x 属于 [1,b / k] ，y属于[1,d / k] 让你求有多少对这样的 （x,y）满足gcd（x,y）== 1 即x和y是互质的。 走到这一步 ，题目算是解决了一半了，我们先来看一下什么是莫比乌斯反演。
这里先给出莫比乌斯的两个公式 ： （以下图片摘自 ACdreamer 的博客，仅供学习交流使用）
OK 这两个就是莫比乌斯反演的两种表现形式 反演的核心所在是莫比乌斯函数，什么是莫比乌斯函数呢？ 我们在下面给出它的定义：
是的 没错 我们称之为 mu 函数，它就是莫比乌斯函数，也是整个反演的最为重要的部分。
现在我们来继续解决上面的那个问题。如何去求有多少对这样的 （x,y）满足gcd（x,y）== 1 。这个问题你直接拿到手发现确实比较麻烦，但是换个思路，如果我们去求有多少对这样的 （x,y）满足 gcd（x,y）== 1 的倍数 呢？ 是不是就非常简单了呢？
OK ！ 我们试着来设一下 F（d）为 有多少对（x,y）满足 gcd（x,y）== d 的倍数 。
f（d）为有多少对（x,y）满足 gcd（x,y）== d 。
呵呵，你发现F（d）用初中数学都能求出是 
(n=b / k，m=d / k)
那么其实我们需要解决的就剩下如何求出 f（1）是多少的问题了。
根据公式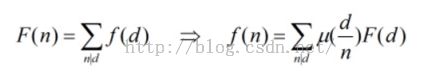
你可以发现，在你对函数进行题设时是需要满足反演对函数的要求的，这个需要你自己来体会，至于另一个公式的设法是 “约数” 的关系，而这个则是 “倍数” 的关系。
那么问题就基本上解决了，f（1）= mu（1）*F（1）+ mu（2）*F（2）+…… 这个式子的终止条件是什么呢？很显然在所限定的区间内，d最大为 min（m,n）。
那么完整的式子就应该是 f（1）= mu（1）*F（1）+ mu（2）*F（2）+……mu（min（m,n））*F（min（m,n））。至此 这道题目就顺利的解决了。
下面给出如何求 mu 函数的代码 下列代码求得了 mu 函数 1-n 的函数值，直接使用就行
第一种 普通筛选求莫比乌斯函数 时间复杂度为 O（nlogn）
void getMu(){
int N=maxn;
for(int i=1;i<N;++i){
int target=i==1?1:0;
int delta=target-mu[i];
mu[i]=delta;
for(int j=2*i;j<N;j+=i)
mu[j]+=delta;
}
} 第二种 线性筛选求莫比乌斯函数 时间复杂度为 O（n）
void Init(){
int N=maxn;
memset(prime,0,sizeof(prime));
memset(mu,0,sizeof(mu));
memset(vis,0,sizeof(vis));
mu[1] = 1;
cnt = 0;
for(int i=2; i<N; i++){
if(!vis[i]){
prime[cnt++] = i;
mu[i] = -1;
}
for(int j=0; j<cnt&&i*prime[j]<N; j++){
vis[i*prime[j]] = 1;
if(i%prime[j]) mu[i*prime[j]] = -mu[i];
else{
mu[i*prime[j]] = 0;
break;
}
}
}
} 此时，走到这一步，我们已经求得了（x,y）满足 gcd（x,y）=1 的对数 ，但题目中说明了，（1，2）和（2，1）算一种情况，那么我们就要减去多余了的情况，怎那么找出那些多算进去的情况呢？ 下面的图画的很清楚：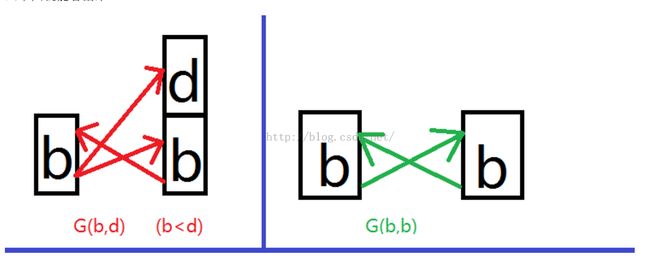
G（b,b）就是多算进去的这些情况，
那么 G（b，d）- G（b，b）/ 2 就是最终我们要求的结果了，至于这一点，有不懂的请在纸上画一画，这不是我要讲的重点了。
完整代码如下：
[cpp] view plain copy
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+7;
bool vis[maxn];
int prime[maxn],mu[maxn];
int cnt;
void Init(){
int N=maxn;
memset(prime,0,sizeof(prime));
memset(mu,0,sizeof(mu));
memset(vis,0,sizeof(vis));
mu[1] = 1;
cnt = 0;
for(int i=2; i<N; i++){
if(!vis[i]){
prime[cnt++] = i;
mu[i] = -1;
}
for(int j=0; j<cnt&&i*prime[j]<N; j++){
vis[i*prime[j]] = 1;
if(i%prime[j]) mu[i*prime[j]] = -mu[i];
else{
mu[i*prime[j]] = 0;
break;
}
}
}
}
void getMu(){
int N=maxn;
for(int i=1;i<N;++i){
int target=i==1?1:0;
int delta=target-mu[i];
mu[i]=delta;
for(int j=2*i;j<N;j+=i)
mu[j]+=delta;
}
}
int main()
{
ios::sync_with_stdio(false);
int a,b,c,d,k;
int T,Case=0;
Init();
cin>>T;
while(T--){
cin>>a>>b>>c>>d>>k;
cout<<"Case "<<++Case<<": ";
if(k==0){
cout<<"0"<<endl;
continue;
}
b/=k,d/=k;
long long ans1=0,ans2=0;
for(int i=1;i<=min(b,d);i++){
ans1+=(long long)mu[i]*(b/i)*(d/i);
}
for(int i=1;i<=min(b,d);i++){
ans2+=(long long)mu[i]*(min(b,d)/i)*(min(b,d)/i);
}
cout<<ans1-ans2/2<<endl;
}
return 0;
} 至此我们通过HDU1695学习了莫比乌斯反演的入门，数论中还有更多有趣的问题等待我们去探索，不得不感叹这些数学家们的伟大了。
该博客转载于lixuepeng_001的博客http://blog.csdn.net/lixuepeng_001/article/details/50577932