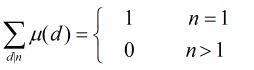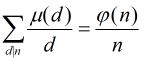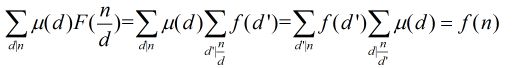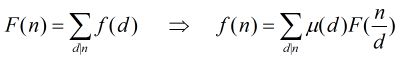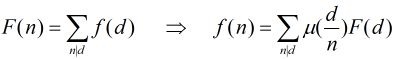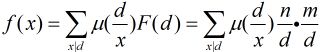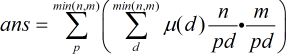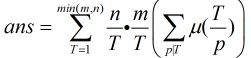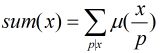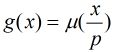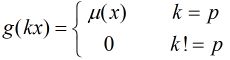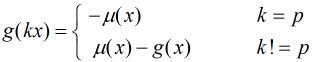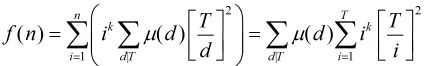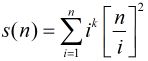莫比乌斯反演

莫比乌斯反演在数论中占有重要的地位，许多情况下能大大简化运算。那么我们先来认识莫比乌斯反演公式。

 

定理：和是定义在非负整数集合上的两个函数，并且满足条件，那么我们得到结论

 

     

 

在上面的公式中有一个函数，它的定义如下：

 

    （1）若，那么

    （2）若，均为互异素数，那么

    （3）其它情况下

 

 

对于函数，它有如下的常见性质：

 

    （1）对任意正整数有

  

                           

 

        （2）对任意正整数有

 

        

 

线性筛选求莫比乌斯反演函数代码。

void Init()
{
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i<N; i++)
    {
        if(!vis[i])
        {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for(int j=0; j<cnt&&i*prime[j]<N; j++)
        {
            vis[i*prime[j]] = 1;
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];
            else
            {
                mu[i*prime[j]] = 0;
                break;
            }
        }
    }
}

 

有了上面的知识，现在我们来证明莫比乌斯反演定理。

 

证明

 

 

证明完毕！

 

嗯，有了莫比乌斯反演，很多问题都可以简化了，接下来我们来看看莫比乌斯反演在数论中如何简化运算的。

 

 

题目：http://bz.cdqzoi.com/JudgeOnline/problem.php?id=2818

 

题意：给一个正整数，其中，求使得为质数的的个数，。

 

分析：对于本题，因为是使得为质数，所以必然要枚举小于等于的质数，那么对于每一个质数，只

     需要求在区间中，满足有序对互质的对数。

 

     也就是说，现在问题转化为：在区间中，存在多少个有序对使得互质，这个问题就简单啦，因为

     是有序对，不妨设，那么我们如果枚举每一个，小于有多少个与互素，这正是欧拉函数。所以

     我们可以递推法求欧拉函数，将得到的答案乘以2即可，但是这里乘以2后还有漏计算了的，那么有哪些呢？

     是且为素数的情况，再加上就行了。

 

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <bitset>

using namespace std;
typedef long long LL;
const int N = 10000010;

bitset<N> prime;
LL phi[N];
LL f[N];
int p[N];
int k;

void isprime()
{
    k = 0;
    prime.set();
    for(int i=2; i<N; i++)
    {
        if(prime[i])
        {
            p[k++] = i;
            for(int j=i+i; j<N; j+=i)
                prime[j] = false;
        }
    }
}

void Init()
{
    for(int i=1; i<N; i++)  phi[i] = i;
    for(int i=2; i<N; i+=2) phi[i] >>= 1;
    for(int i=3; i<N; i+=2)
    {
        if(phi[i] == i)
        {
            for(int j=i; j<N; j+=i)
                phi[j] = phi[j] - phi[j] / i;
        }
    }
    f[1] = 0;
    for(int i=2;i<N;i++)
        f[i] = f[i-1] + (phi[i]<<1);
}

LL Solve(int n)
{
    LL ans = 0;
    for(int i=0; i<k&&p[i]<=n; i++)
        ans += 1 + f[n/p[i]];
    return ans;
}

int main()
{
    Init();
    isprime();
    int n;
    scanf("%d",&n);
    printf("%I64d\n",Solve(n));
    return 0;
}

 

嗯，上题不算太难，普通的欧拉函数就可以搞定，接下来我们来看看它的升级版。

 

题意：给定两个数和，其中，，求为质数的有多少对？其中和的范

     围是。

 

分析：本题与上题不同的是和不一定相同。在这里我们用莫比乌斯反演来解决，文章开头也说了它能大大简化

     运算。我们知道莫比乌斯反演的一般描述为：

 

    

 

     其实它还有另一种描述，本题也是用到这种。那就是：

 

     

 

     好了，到了这里，我们开始进入正题。。。

 

     对于本题，我们设

 

     为满足且和的的对数

     为满足且和的的对数

 

     那么，很显然，反演后得到

 

     因为题目要求是为质数，那么我们枚举每一个质数，然后得到

 

    

 

     如果直接这样做肯定TLE，那么我们必须优化。

 

     我们设，那么继续得到。

 

     到了这里，可以看出如果我们可以先预处理出所有的对应的的值，那么本题就解决了。

 

     我们设，注意这里为素数，。

 

     那么，我们枚举每一个，得到，现在分情况讨论：

 

     （1）如果整除，那么得到

 

      

 

     （2）如果不整除，那么得到

 

       

 

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
typedef long long LL;
const int N = 10000005;

bool vis[N];
int p[N];
int cnt;
int g[N],u[N],sum[N];

void Init()
{
    memset(vis,0,sizeof(vis));
    u[1] = 1;
    cnt = 0;
    for(int i=2;i<N;i++)
    {
        if(!vis[i])
        {
            p[cnt++] = i;
            u[i] = -1;
            g[i] = 1;
        }
        for(int j=0;j<cnt&&i*p[j]<N;j++)
        {
            vis[i*p[j]] = 1;
            if(i%p[j])
            {
                u[i*p[j]] = -u[i];
                g[i*p[j]] = u[i] - g[i];
            }
            else
            {
                u[i*p[j]] = 0;
                g[i*p[j]] = u[i];
                break;
            }
        }
    }
    sum[0] = 0;
    for(int i=1;i<N;i++)
        sum[i] = sum[i-1] + g[i];
}

int main()
{
    Init();
    int T;
    scanf("%d",&T);
    while(T--)
    {
        LL n,m;
        cin>>n>>m;
        if(n > m) swap(n,m);
        LL ans = 0;
        for(int i=1,last;i<=n;i=last+1)
        {
            last = min(n/(n/i),m/(m/i));
            ans += (n/i)*(m/i)*(sum[last]-sum[i-1]);
        }
        cout<<ans<<endl;
    }
    return 0;
}

(2)

题意：给定N,M，求满足1<=i<=N,1<=j<=M,gcd(i,j)为质数的有序数对(i,j)的对数，N,M<=10^7 测试数据组数<=10^4

莫比乌斯反演好神奇...

一直只知道百度百科上说的那一种形式：若F(n)=Σ(d|n)f(d)则f(n)=Σ(d|n)miu(d)F(n/d)

查了题解才知道有另一种形式...也就是这道题会用到的形式...

若F(x)=Σ(x|d)f(d)则f(x)=Σ(x|d)miu(d/x)F(d) 其中d在某个限定范围内，接下来的问题就是：

对于给定的N,M，求1<=i<=N,1<=j<=M,gcd(i,j)=1的有序数对(i,j)的对数。再枚举质数p后，把N'=N/p,M'=M/p时这个问题的解累加起来就可以了。

对于给定的N,M，设f(x)为1<=i<=N,1<=j<=M,gcd(i,j)=x的(i,j)的对数，F(x)为1<=i<=N,1<=j<=M,x|gcd(i,j)的(i,j)的对数。

显然有F(x)=(N/x)*(M/x) (N/x和M/x都是下取整)      F(x)=Σ(x|d)f(d)

反演得到
                 f(x)=Σ(x|d)miu(d/x)F(d)=Σ(x|d)miu(d/x)*(N/d)*(M/d)

这个问题的解是f(1)，把x=1代入得到 ：f(1)=Σ(d)miu(d)*(N/d)*(M/d)

做完了?当然没有。不TLE见鬼了。考察答案的表达式：Ans=Σ(质数p) [ Σ(d)miu(d)*(N/pd)*(M/pd) ]

换个角度，先枚举T=pd，再去枚举p，则d=T/p。得到Ans=∑(T) [ ∑(质数p|T)miu(T/p)*(N/T)*(M/T) ]

这么做的好处立刻就显现出来了，N/T和M/T与p无关!

Ans=∑(T) [ (N/T)*(M/T) *∑(质数p|T)miu(T/p) ]

再令g(x)=sigma(质数p|x)miu(x/p) 改写上式为

Ans=∑(T)(N/T)*(M/T)*g(T) 

恩，非常和谐。

接下来全副精力对付g(x)。仍然考虑线性筛搞定他。

假设枚举到i，质数枚举到p(程序里的prime[j])，要更新A=i*p的信息。

1. p|i
    这时A的素数分解式中，p这一项的次数>=2。

  考虑g(A)的求和式：

  如果枚举的质数p'不等于p，A/p'就也会有p这一项，次数>=2，这时候miu(A/p')=0

    如果枚举的质数p'=p，A/p=i，这一项就是miu(i)

    因此g(A)=miu(i)
2. p!|i (即i%p!=0）

   这时候A比i多一个质因子p，对miu(i)分情况讨论。

  2.1 miu(i)==0 (即i有大于1次的项)

           这时A除去任何一个p'都会留下i的那个大于1次的项，除非是下面这一种非常特殊的情况：

    2.1.1 i的素数分解式中，大于1次的项只有一个，且这一项为2次。记这一项为p0。

         这时除去任何一个p'!=p0都会留下这一项，但是除去p0则会得到A/p0——这个数所有的项都是1次的。因此g(A)=miu(A/p0)

          2.1.2 i的素数分解式大于1次的项不止一个 或者 大于1次的项唯一，但次数高于2次。易见g(A)=0

     2.2 miu(i)!=0 (即i全是1次) 这个时候A的项也全是1次。设r(x)为x的质因子个数。

     则可以得到g(A)=r(A)*(-1)^(r(A)-1)。因为除以任何一个p'，miu(A/p')都是一样的。

     同理g(i)=r(i)*(-1)^(r(i)-1)，且有r(A)=r(i)+1。 利用r(A)=r(i)+1可以方便地得到：g(A)和g(i)异号，且绝对值比g(i)多1。

     亦即g(A)=(g(i)>0)?-1:1 -g(i) 

          g(A)的维护讨论完了。

完了?没完，看情况2.1.1，我们有这么个遗留问题：

如果x的大于1次的项唯一，且这一项为2次，则令f(x)为这个项，否则f(x)=1。

事实上f(x)=1包含3种情况：

1. 大于1的项不唯一

2. 大于1次的项唯一但大于2次。

3. 全为1次

1和2利用现有的结果无法区分，但事实上不需要区分。3则可以用miu(x)判出来。

好，我们来对付f(x)，仍然是线性筛，变量意义同g(x)的讨论。

1. p|i

 A由i把最小因子p的次数加1得到，显然这一项的次数>=2。

1.1 f(i)!=1 

1.1.1 如果f(i)=p，那么A中p的次数就是3次了，f(A)=1。

1.1.2 如果f(i)!=p，那么A中大于1次的项就不唯一了，仍有f(A)=1

因此f(i)!=1必然有f(A)=1

1.2 i全为1次 即f(i)=1且miu(i)!=0 这时显然f(A)=p

1.3 i不全为1次 即f(i)=1且miu(i)=0 这时显然f(A)=1

2. p!|i

A比i多一个1次的质因数p，那么应有f(A)=f(i)

f(A)的递推也讨论完了。

完了?虽然剩下的工作很简单但是也是必不可少的..

回去看求和的式子：Ans=∑(T)(N/T)*(M/T)*g(T)

直接做是O(min(M,N))的，别忘了有1W组数据啊。

但是我们有个结论：对于给定的N，(N/T)的取值只有sqrt(N)个

那么给定的N,M，(N/T)*(M/T)就只有sqrt(N)+sqrt(M)个了，而且相同的取值当然是连成一段的。

由此，分段来计算。令gs(x)为g(x)的前缀和。

对于枚举到的i，我们希望找到最大的使得(N/i)*(M/i)=(N/j)*(M/j)的j值。

这可能有点困难，我们退而求其次，求出最大的使得N/i=N/j且M/i=M/j的j值，效果不会变差太多。

这个就很简单了，可以得到j=min(N/(N/i),M/(M/i))。于是把i~j这一段整体计算即可。

 #include <cstdio>
 #include<algorithm>
 #include<cstdlib>
 #include<cstring>
 const int maxp=10000001;
 int pr[maxp],miu[maxp],g[maxp],f[maxp];
 long long gs[maxp];
 bool flag[maxp];
 int gcd(int x,int y)
 {
     int t;
     if(x<y)
     {
         t=x;
         x=y;
         y=t;
     }
     while(y)
     {
         t=x%y;
         x=y;
         y=t;
     }
     return x;
 }

 void init()
 {
     int i,j,A;
     miu[1]=1;
     for(i=2;i<maxp;++i)
     {
         if(!flag[i])
         {
             pr[++pr[0]]=i;
             miu[i]=-1;
             f[i]=g[i]=1;
         }
         for(j=1;j<=pr[0]&&i*pr[j]<maxp;++j)
         {
             flag[A=i*pr[j]]=true;
             if(i%pr[j]!=0)
             {
                 miu[A]=-miu[i];
                 f[A]=f[i];
                 if(miu[i]==0)
                      g[A]=(f[i]!=1)?miu[A/f[i]]:0;
                 else
                      g[A]=(g[i]>0)?(-g[i]-1):(-g[i]+1);
             }
             else
             {
                 miu[A]=0;
                 if(f[i]==1)
                      f[A]=(miu[i]==0)?1:pr[j];
                 else
                      f[A]=1;
                 g[A]=miu[i];
                 break;
             }
         }
     }
     for(i=2;i<maxp;++i)
          gs[i]=gs[i-1]+g[i];
 }

 int main()
 {
     init();
     int T,N,M,i,j,t,t1,t2;
     long long ans;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&N,&M);
         if(N<M){t=N;N=M;M=t;}
         ans=0;
         for(i=2;i<=M;i=t+1)
         {
             t1=N/(N/i);
             t2=M/(M/i);
             t=(t1<t2)?t1:t2;
             ans+=(gs[t]-gs[i-1])*(N/i)*(M/i);
         }
         printf("%lld\n",ans);
     }
     return 0;
 }

题目：http://acm.uestc.edu.cn/#/problem/show/811

 

题意：给定两个正整数和，其中，，求的值，其中。

 

分析：本题是典型的莫比乌斯反演问题。那么，怎么反演呢？

     首先，我们枚举的所有值，根据以前学的莫比乌斯反演，可以很容易得到

 

     ，其中

 

     我们设

 

     ，那么得到，反演后得到

 

     所以就是

 

     可以看出枚举的所有因子递归下去就行。。。现在的关键问题是如何计算。

 

     的表达式为

 

     由于不大，所以可以直接用自然数幂和，而在一段连续的区间值保持不变，思路跟下面这道题差不多。

 

     题目：http://blog.csdn.net/acdreamers/article/details/10249611

 

      也就是说的时间复杂度为。加上递归的部分，本题总的时间复杂度为。

 

 

     代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>

using namespace std;
const int N = 50000005;
typedef long long LL;
const LL MOD = 1000000007;

LL dp[N];

LL mu(LL n,int k)
{
    LL ans = 1;
    for(int i=0; i<k; i++)
    {
        ans *= n;
        ans %= MOD;
    }
    return ans;
}

LL calc(LL n,int k)
{
    if(k == 1) return ((n%MOD)*((n+1)%MOD))%MOD*500000004%MOD;
    if(k == 2)
    {
        LL a = n % MOD;
        LL b = (n+1) % MOD;
        LL c = (2*n+1) % MOD;
        return a*b%MOD*c%MOD*166666668%MOD;
    }
    if(k == 3)
    {
        LL t = ((n%MOD)*((n+1)%MOD))%MOD*500000004%MOD;
        return t * t % MOD;
    }
    if(k == 4)
    {
        LL t = 6*mu(n,5)%MOD + 15*mu(n,4)%MOD + 10*mu(n,3)%MOD -n%MOD;
        t %= MOD;
        t += MOD;
        t %= MOD;
        t *= 233333335;
        t %= MOD;
        return t;
    }
    if(k == 5)
    {
        LL t = 2*mu(n,6)%MOD + 6*mu(n,5)%MOD + 5*mu(n,4)%MOD -mu(n,2)%MOD;
        t %= MOD;
        t += MOD;
        t %= MOD;
        t *= 83333334;
        t %= MOD;
        return t;
    }
}

LL sum(LL n,int k)
{
    LL ans = 0;
    LL T = (LL)sqrt(1.0*n);
    for(int i=1; i<=T; i++)
    {
        LL t = (n/i) % MOD;
        LL a = t * t % MOD;
        LL b = mu(i,k) * a % MOD;
        LL c = i * i % MOD;
        LL L = n/(i+1) + 1;
        LL R = n/i;
        LL d = calc(R,k) - calc(L-1,k);
        d %= MOD;
        d += MOD;
        d %= MOD;
        c = c * d % MOD;
        ans += b + c;
        ans %= MOD;
    }
    if(T*T == n)
        ans -= mu(T,k+2);
    ans %= MOD;
    ans += MOD;
    ans %= MOD;
    return ans;
}

LL dfs(LL n,int k)
{
    if(n < N && dp[n]) return dp[n];
    if(n == 1) return 1;
    LL ans = sum(n,k);
    LL tmp = 0;
    for(LL i=1; i*i<=n; i++)
    {
        if(i*i == n)
        {
            tmp %= MOD;
            tmp += dfs(i,k);
            tmp %= MOD;
        }
        else
        {
            tmp %= MOD;
            tmp += dfs(i,k);
            tmp %= MOD;
            if(i == 1) continue;
            tmp += dfs(n/i,k);
            tmp %= MOD;
        }
    }
    if(n < N)
        dp[n] = ((ans-tmp)%MOD + MOD) % MOD;
    return ((ans-tmp)%MOD + MOD) % MOD;
}

int main()
{
    LL n,k;
    memset(dp,0,sizeof(dp));
    scanf("%lld%lld",&n,&k);
    printf("%lld\n",dfs(n,k));
    return 0;
}