人工智能必备数学基础--精华笔记
人工智能必备数学基础--笔记
- 废话
- 笔记
- 高等数学基础
- 函数
- 极限
- 函数的连续性
- 导数
- 偏导数
- 方向导数
- 梯度
- 微积分
- 求曲边面积
- 定积分
- 第一中值定理
- 牛顿—莱布尼茨公式
- 泰勒公式与拉格朗日
- 泰勒公式出发点(函数化简)
- 以直代曲
- 一点一世界
- 泰勒多项式
- 推导变换过程
- 麦克劳林公式
- 多项式逼近
- 阶数
- 阶乘
- 拉格朗日乘子法(求满足约束时函数极值)
- 线性代数基础
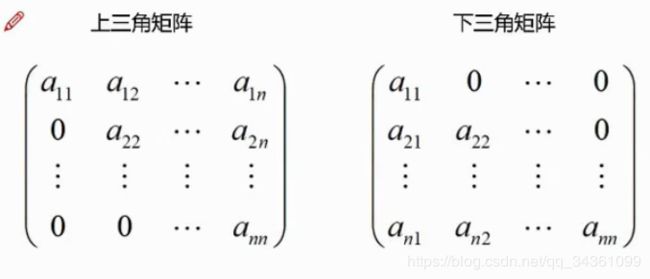
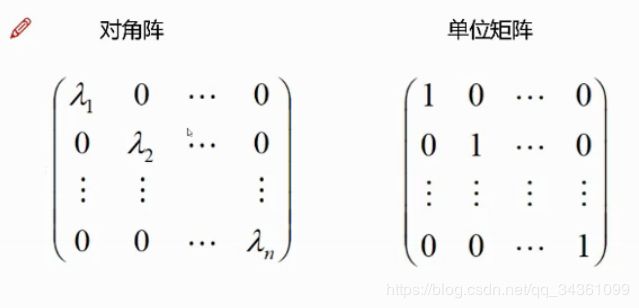
- 矩阵与行列式的区别
- 矩阵类型
- 矩阵操作
- 矩阵的秩
- 向量的内积
- 向量的长度
- 向量的正交
- 特征值与矩阵分解
- 特征值与特征向量
- Continuously Updating……
废话
听说这年头博客和github跟名片一样?那我干脆把笔记记在博客好了,反正云上笔记也不容易丢。课程跟的是唐宇迪的人工智能必备数学基础,主要记录一些自己的理解和搜集的有助于理解的资料,方便回顾时迅速get到要点。网课CSDN学院,网易云课堂和腾讯课堂都有(mai bu qi de hua dao ban ye you),鼓励各位支持正版哈,授课老师属于少数的不废话的好老师。回归正题,研究ML(机器学习)、DL(深度学习)方面的童鞋没有数学支撑的话读论文或者搞创新都是很吃力的,磨刀不误砍柴工。
笔记
高等数学基础
函数
- y = f ( x ) x : 自 变 量 y : 因 变 量 y = f(x) x:自变量 y:因变量 y=f(x) x:自变量 y:因变量
- 函 数 值 表 达 形 式 : y 0 = y ∣ x = x 0 = f ( x 0 ) 函数值表达形式:y_0 = y\mid_x=x_0 = f(x_0) 函数值表达形式:y0=y∣x=x0=f(x0)
- 函 数 俩 种 表 达 式 : 函数俩种表达式: 函数俩种表达式:eg.
显 函 数 y = x 2 + 1 显函数 y = x^2+1 显函数y=x2+1
隐 函 数 F ( x , y ) = 0 即 x 2 − y + 1 = 0 隐函数 F(x, y) = 0 即 x^2-y+1 = 0 隐函数F(x,y)=0即x2−y+1=0 - 偶 函 数 : f ( − x ) = f ( x ) 偶函数:f(-x) = f(x) 偶函数:f(−x)=f(x)
- 奇 函 数 : f ( − x ) = − f ( x ) 奇函数:f(-x) = -f(x) 奇函数:f(−x)=−f(x)
- 周 期 性 : f ( x + T ) = f ( x ) 周期性:f(x+T) = f(x) 周期性:f(x+T)=f(x)
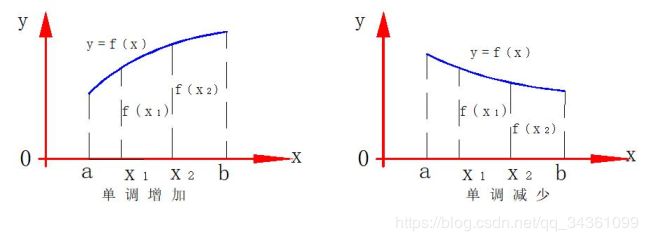
- 单 调 性 : 单调性: 单调性:
极限
-
数列:u1,u2,u3,…,un ,… 其中un叫做通项
n → ∞ \infty ∞ 时,若通项趋近于常数C,则称数列收敛于A否则称数列为发散 -
趋近符号含义
x → x 0 : 当 x 从 x 0 两 侧 趋 近 于 x 0 时 x → x_0:当x从x_0两侧趋近于x_0时 x→x0:当x从x0两侧趋近于x0时
x → x 0 + : 当 x 从 x 0 右 侧 趋 近 于 x 0 时 x → x_0^+:当x从x~0~右侧趋近于x_0时 x→x0+:当x从x 0 右侧趋近于x0时
x → x 0 − : 当 x 从 x 0 左 侧 趋 近 于 x 0 时 x → x_0^-:当x从x~0~左侧趋近于x_0时 x→x0−:当x从x 0 左侧趋近于x0时 -
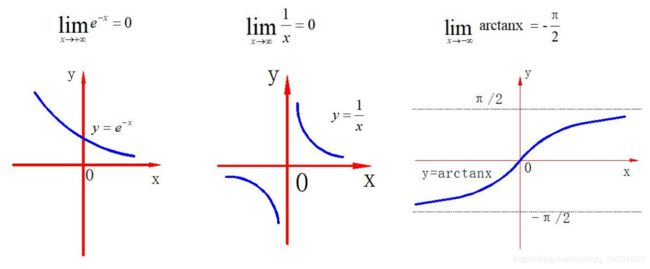
无穷小
以零为极限 eg.
lim Δ x → ∞ 1 x = 0 , 则 1 x 是 x → ∞ 时 的 无 穷 小 \lim_{\Delta x\to \infty}\frac{1}{x}=0,则\frac{1}{x}是x\rightarrow\infty时的无穷小 limΔx→∞x1=0,则x1是x→∞时的无穷小
lim Δ x → 2 ( 3 x − 6 ) = 0 , 则 3 x − 6 是 x → 2 时 的 无 穷 小 \lim_{\Delta x\to 2}(3x-6)=0,则3x-6是x\rightarrow2时的无穷小 limΔx→2(3x−6)=0,则3x−6是x→2时的无穷小①无限个无穷小之和不一定是无穷小。
lim n → ∞ ( 1 n 2 + 2 n 2 + … + n n 2 ) = lim n → ∞ n ( n + 1 ) 2 n 2 = lim n → ∞ n + 1 2 n = 1 2 \lim_{n\to\infty}(\frac{1}{n^2}+\frac{2}{n^2}+…+\frac{n}{n^2})=\lim_{n\to\infty}\frac{\frac{n(n+1)}{2}}{n^2}=\lim_{n\to\infty}\frac{n+1}{2n}=\frac{1}{2} limn→∞(n21+n22+…+n2n)=limn→∞n22n(n+1)=limn→∞2nn+1=21②无穷小的商不一定是无穷小。
lim x → 0 x 2 x = 1 2 lim x → 0 x 2 2 x = 0 lim x → 0 2 x x 2 = ∞ \lim_{x\to0}\frac{x}{2x}=\frac{1}{2} \lim_{x\to0}\frac{x^2}{2x}=0 \lim_{x\to0}\frac{2x}{x^2}=\infty limx→02xx=21 limx→02xx2=0 limx→0x22x=∞③无穷小的比较
lim x → x 0 α ( x ) = 0 lim x → x 0 β ( x ) = 0 \lim_{x\to x_0}\alpha(x)=0 \lim_{x\to x_0}\beta(x)=0 limx→x0α(x)=0 limx→x0β(x)=0l i m x → x 0 α ( x ) β ( x ) = 0 , 则 α 比 β 高 阶 lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=0,则\alpha比\beta高阶 limx→x0β(x)α(x)=0,则α比β高阶
l i m x → x 0 α ( x ) β ( x ) = ∞ , 则 α 比 β 低 阶 lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=\infty,则\alpha比\beta低阶 limx→x0β(x)α(x)=∞,则α比β低阶
l i m x → x 0 α ( x ) β ( x ) = C ≠ 0 , 则 α 与 β 同 阶 lim_{x\to x_0}\frac{\alpha(x)}{\beta(x)}=C≠0,则\alpha与\beta同阶 limx→x0β(x)α(x)=C̸=0,则α与β同阶
函数的连续性
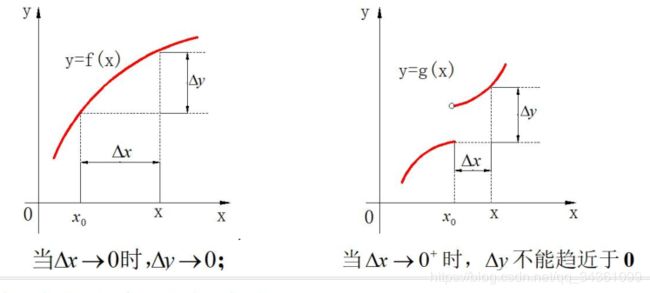
设 函 数 f ( x ) 在 点 x 0 的 某 邻 域 内 有 定 义 , 如 果 当 自 变 量 的 改 变 量 △ x 趋 近 于 零 时 , 相 应 函 数 的 改 变 量 △ y 也 趋 近 于 零 , 则 称 y = f ( x ) 在 点 x 0 处 连 续 设函数f (x)在点x_0的某邻域内有定义,如果当自变量的改变量△x趋近于 零时,相应函数的改变量△y也趋近于零,则称y = f (x)在点 x_0处连续 设函数f(x)在点x0的某邻域内有定义,如果当自变量的改变量△x趋近于零时,相应函数的改变量△y也趋近于零,则称y=f(x)在点x0处连续
条件
- 函数在该点处有定义
- 函数在该点处极限存在
- 极限值等于函数值
导数
如 果 平 均 变 化 率 的 极 限 存 在 lim x → 0 Δ x Δ y = lim x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x 如果平均变化率的极限存在\lim_{x\to 0}\frac{\Delta x}{\Delta y}=\lim_{x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} 如果平均变化率的极限存在limx→0ΔyΔx=limx→0Δxf(x0+Δx)−f(x0)
则 称 此 极 限 为 函 数 y = f ( x ) 在 点 x 0 处 的 导 数 , f ′ ( x 0 ) , y ′ ∣ x = x 0 , d y d x ∣ x = x 0 , d f ( x ) d x ∣ x = x 0 则称此极限为函数y=f(x)在点x_0处的导数,f'(x_0),y'\mid_{x=x_0},\frac{dy}{dx}\mid_{x=x_0},\frac{df(x)}{dx}\mid_{x=x_0} 则称此极限为函数y=f(x)在点x0处的导数,f′(x0),y′∣x=x0,dxdy∣x=x0,dxdf(x)∣x=x0
偏导数
设 函 数 z = f ( x , y ) 在 点 ( x 0 , y 0 ) 的 某 个 邻 域 内 有 定 义 , 设函数z=f(x,y)在点(x_0,y_0)的某个邻域内有定义, 设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义, 定 y = y 0 定y=y_0 定y=y0 , 一 元 函 数 f ( x , y 0 ) 在 点 x = x 0 处 可 导 , 即 极 限 lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = A , 则 称 A 为 函 数 : z = f ( x , y ) 在 点 ( x 0 , y 0 ) 处 关 于 自 变 量 x 的 偏 导 数 , 记 作 f x ( x 0 , y 0 ) 或 ∂ z ∂ x ∣ x = x 0 , ∂ f ∂ x ∣ x = x 0 , Z x ∣ x = x 0 ,一元函数f(x,y_0)在点x=x_0处可导,即极限\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=A,则称A为函数:z=f(x,y)在点(x_0,y_0)处关于自变量x的偏导数,记作f_x(x_0,y_0)或\frac{\partial z}{\partial x}\mid_{x=x_0},\frac{\partial f}{\partial x}\mid_{x=x_0},Z_x\mid_{x=x_0} ,一元函数f(x,y0)在点x=x0处可导,即极限limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)=A,则称A为函数:z=f(x,y)在点(x0,y0)处关于自变量x的偏导数,记作fx(x0,y0)或∂x∂z∣x=x0,∂x∂f∣x=x0,Zx∣x=x0
几何意义
∂ ∂ x f ( x , y 0 ) ∣ x = x 0 是 曲 线 y = { z = f ( x , y ) y = y 0 在 点 M 0 处 的 切 线 M 0 T x 对 x 轴 的 斜 率 \frac{\partial}{\partial x}f(x,y_0)\mid_{x=x0} 是曲线 y =\begin{cases} z=f (x,y)\\ y=y_0 \end{cases}在点M_0处的切线M_0T_x对x轴的斜率 ∂x∂f(x,y0)∣x=x0是曲线y={z=f(x,y)y=y0在点M0处的切线M0Tx对x轴的斜率
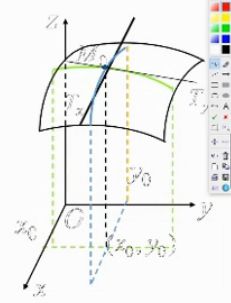
e g . 求 f ( x , y ) = x 2 + 3 x y + y 2 在 点 ( 1 , 2 ) 处 的 偏 导 数 eg.求f(x,y)=x^2+3xy+y^2在点(1,2)处的偏导数 eg.求f(x,y)=x2+3xy+y2在点(1,2)处的偏导数
f x ( x , y ) = 2 x + 3 y f x ( 1 , 2 ) = 8 f_x(x,y)=2x+3y f_x(1,2)=8 fx(x,y)=2x+3y fx(1,2)=8
f y ( x , y ) = 3 x + 2 y f y ( 1 , 2 ) = 7 f_y(x,y)=3x+2y f_y(1,2)=7 fy(x,y)=3x+2y fy(1,2)=7
方向导数
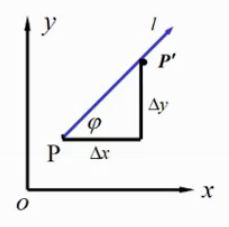 设 l l l 为任意一个方向向量
设 l l l 为任意一个方向向量
z = f ( x , y ) z=f(x,y) z=f(x,y)
∂ f ∂ l = lim ρ → 0 f ( x + Δ x , y + Δ y ) − f ( x , y ) ρ = Δ x 2 + Δ y 2 = ∂ f ∂ x cos ψ + ∂ f ∂ y sin ψ \frac{\partial f}{\partial l}=\lim_{\rho\to0}\frac{f(x+\Delta x,y+\Delta y)-f(x,y)}{\rho=\sqrt{\Delta x^2+\Delta y^2}}=\frac{\partial f}{\partial x}\cos \psi+\frac{\partial f}{\partial y}\sin \psi ∂l∂f=limρ→0ρ=Δx2+Δy2f(x+Δx,y+Δy)−f(x,y)=∂x∂fcosψ+∂y∂fsinψ
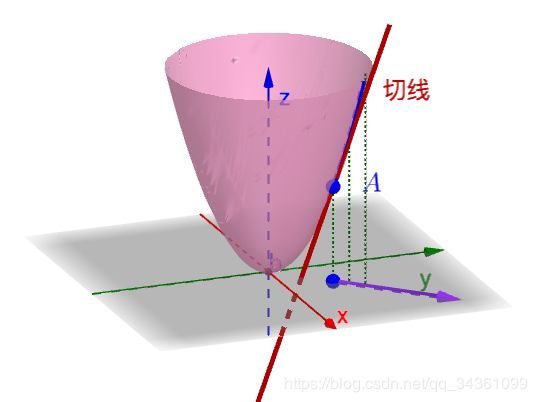
方 向 导 数 为 某 一 方 向 向 量 l 所 在 平 面 与 函 数 相 交 形 成 的 曲 线 在 x 0 处 的 导 数 方向导数为某一方向向量l所在平面与函数相交形成的曲线在x_0处的导数 方向导数为某一方向向量l所在平面与函数相交形成的曲线在x0处的导数
偏 导 数 是 l 为 坐 标 轴 方 向 的 方 向 导 数 偏导数是l为坐标轴方向的方向导数 偏导数是l为坐标轴方向的方向导数
梯度
函数在某点的梯度是一个方向向量(x,y),它的方向等于方向导数最大值取得的方向一致,其大小正好是最大的方向导数 eg.

2019.1.13 7:28
微积分
求曲边面积
-
微分矩形:把曲面分为无穷个小矩形,则曲面面积近似于无数个小矩形面积的总和
S = ∫ a b f ( x ) Δ x ( 当 Δ x → 0 时 , ξ = f ( x ) ) S=\int_a^bf(x)\Delta x (当\Delta x\to0时,\xi=f(x)) S=∫abf(x)Δx (当Δx→0时,ξ=f(x)) -
函数意义替换:把 f ( x ) f(x) f(x)当作 F ( x ) F(x) F(x)的导函数 F ′ ( x ) F'(x) F′(x),则
f ( x ) 在 Δ x 上 的 积 分 ∫ a b f ( x ) d x f(x)在\Delta x上的积分\int_a^bf(x)dx f(x)在Δx上的积分∫abf(x)dx
= F ′ ( x ) 的 积 分 ∫ a b F ′ ( x ) d x =F'(x)的积分\int_a^bF'(x)dx =F′(x)的积分∫abF′(x)dx
= ∫ a b d y d x ⋅ d x = ∫ a b d y ( d x → 0 ) =\int_a^b\frac{dy}{dx}\cdot dx=\int_a^bdy (dx\to0) =∫abdxdy⋅dx=∫abdy (dx→0)
≈ 函 数 F ( x ) 在 [ a , b ] 区 间 的 增 量 ∫ a b Δ y ≈函数F(x)在[a,b]区间的增量\int_a^b\Delta y ≈函数F(x)在[a,b]区间的增量∫abΔy
= F ( b ) − F ( a ) =F(b)-F(a) =F(b)−F(a)
导函数线下面积=原函数改变量
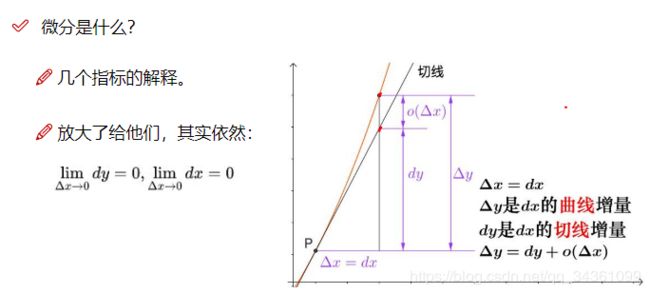
x → 0 时 , Δ y = d y x\to0时,\Delta y=dy x→0时,Δy=dy
定积分
第一中值定理

ξ 左 移 , 求 得 的 S 偏 小 ξ 右 移 , 求 得 的 S 偏 大 \xi左移,求得的S偏小 \xi右移,求得的S偏大 ξ左移,求得的S偏小 ξ右移,求得的S偏大
故 必 存 在 ξ , 使 求 得 的 S 刚 刚 好 故必存在\xi,使求得的S刚刚好 故必存在ξ,使求得的S刚刚好
牛顿—莱布尼茨公式

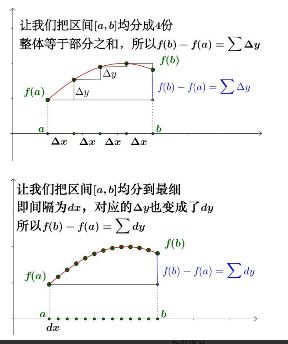 图 中 f ( x ) 表 示 上 述 F ( x ) 图中f(x)表示上述F(x) 图中f(x)表示上述F(x)
图 中 f ( x ) 表 示 上 述 F ( x ) 图中f(x)表示上述F(x) 图中f(x)表示上述F(x)
eg.
2019.2.4 3:48
泰勒公式与拉格朗日
泰勒公式出发点(函数化简)
- 用简单的熟悉的多项式来近似代替复杂的函数
- 易计算函数值,导数与积分仍是多项式多项式由它的系数完全确定,其系数又由它在一点的函数值及其导数所确定。易计算函数值,导数与积分仍是多项式
- 多项式由它的系数完全确定,其系数又由它在一点的函数值及其导数所确定。多项式由它的系数完全确定,其系数又由它在一点的函数值及其导数所确定。
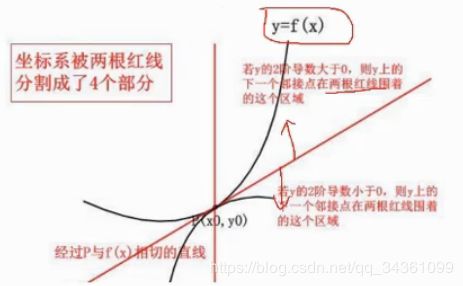
以直代曲
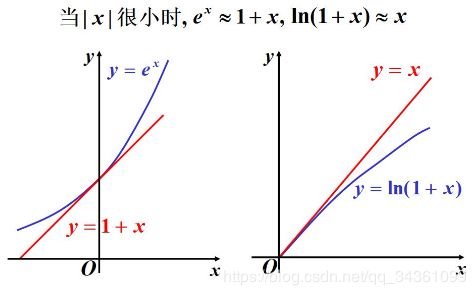
当 ( x − x 0 ) → 0 时 , f ( x ) = f ( x 0 ) + ∫ x 0 x f ′ ( x ) ( x − x 0 ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) 当(x-x_0)\to0时,f(x)=f(x_0)+\int_{x_0}^xf'(x)(x-x_0)≈f(x_0)+f'(x_0)(x-x_0) 当(x−x0)→0时,f(x)=f(x0)+∫x0xf′(x)(x−x0)≈f(x0)+f′(x0)(x−x0)
一点一世界
泰勒多项式
P n ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + … + f ( n ) ( x 0 ) n ! ( x − x 0 ) n P_n(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)}{2!}(x-x_0)^2+…+\frac{f^{(n)}(x0)}{n!}(x-x_0)^n Pn(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+…+n!f(n)(x0)(x−x0)n
称 为 f ( x ) 在 x 0 关 于 ( x − x 0 ) 的 n 阶 泰 勒 多 项 式 称为f(x)在x_0关于(x-x_0)的n阶泰勒多项式 称为f(x)在x0关于(x−x0)的n阶泰勒多项式
推导变换过程
f ( a + Δ x ) = f ( a ) + ∫ a a + Δ x f ′ ( x ) d x ( 牛 顿 — 莱 布 尼 茨 公 式 ) f(a+\Delta x)=f(a)+\int_a^{a+\Delta x}f'(x)dx (牛顿—莱布尼茨公式) f(a+Δx)=f(a)+∫aa+Δxf′(x)dx (牛顿—莱布尼茨公式)
= f ( a ) + f ′ ( a ) Δ x + f ′ ′ ( a ) 2 Δ x 2 + ∫ 0 Δ x ∫ a a + t ∫ a a + t 1 f ′ ′ ′ ( x ) d x d x d t ( 换 元 x = a + t ) =f(a)+f'(a)\Delta x+\frac{f''(a)}{2}\Delta x^2+\int_0^{\Delta x}\int_a^{a+t}\int_a^{a+t_1}f'''(x)dxdxdt (换元x=a+t) =f(a)+f′(a)Δx+2f′′(a)Δx2+∫0Δx∫aa+t∫aa+t1f′′′(x)dxdxdt (换元x=a+t)
具体过程请参考这篇博客
任意多阶可导函数可被展开为泰勒多项式以简化函数表达
麦克劳林公式
指定 x 0 = 0 的 泰 勒 公 式 x_0=0的泰勒公式 x0=0的泰勒公式
f ( x ) = f ( 0 ) + f ′ ( x ) x + f ′ ′ ( 0 ) 2 ! x 2 + … + f ( n ) ( 0 ) n ! x n + f ( n + 1 ) ( θ x ) ( n + 1 ) ! x n + 1 ( 0 < θ < 1 ) f(x)=f(0)+f'(x)x+\frac{f''(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n+\frac{f^{(n+1)(\theta x)}}{(n+1)!}x^{n+1}(0<\theta<1) f(x)=f(0)+f′(x)x+2!f′′(0)x2+…+n!f(n)(0)xn+(n+1)!f(n+1)(θx)xn+1(0<θ<1)
f ( x ) ≈ f ( 0 ) + f ′ ( x ) x + f ′ ′ ( 0 ) 2 ! x 2 + … + f ( n ) ( 0 ) n ! x n f(x)≈f(0)+f'(x)x+\frac{f''(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n f(x)≈f(0)+f′(x)x+2!f′′(0)x2+…+n!f(n)(0)xn
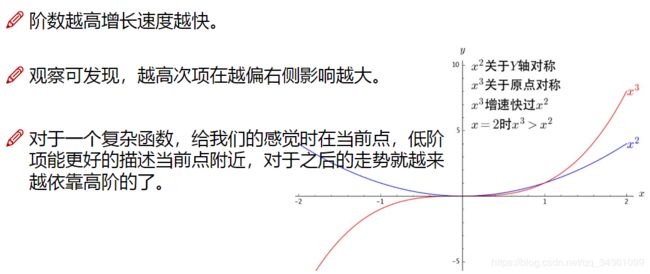
多项式逼近
多阶导数的意义
eg. f ( x ) = e x f(x)=e^x f(x)=ex

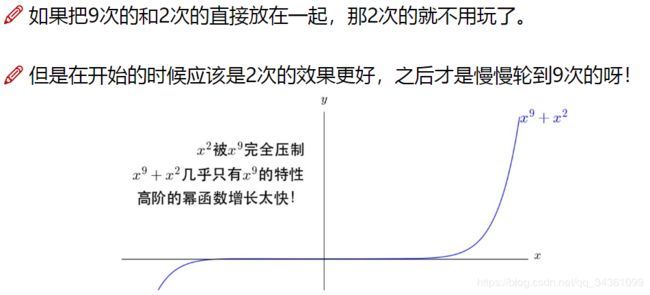
阶数
阶乘
拉格朗日乘子法(求满足约束时函数极值)
函 数 : f ( x , y ) 约 束 : g ( x , y ) = C 求 满 足 约 束 条 件 的 函 数 极 值 函数:f(x,y) 约束:g(x,y)=C 求满足约束条件的函数极值 函数:f(x,y) 约束:g(x,y)=C 求满足约束条件的函数极值

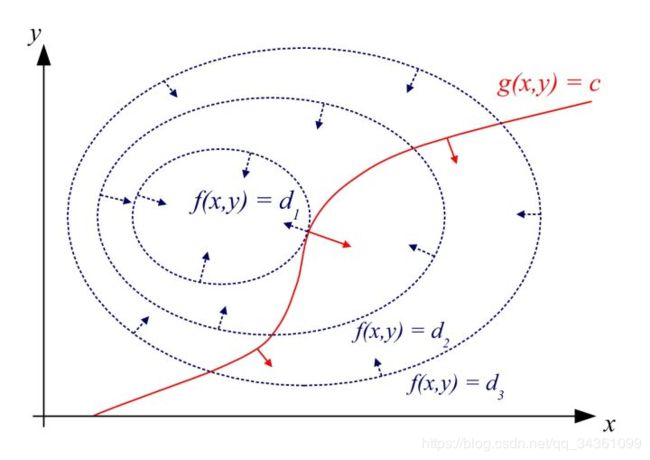
当 二维曲线 g ( x , y ) = C g(x,y)=C g(x,y)=C 与函数 z = f ( x , y ) z=f(x,y) z=f(x,y) 的某条等高线(也是 二维曲线 ) f ( x , y ) = d ( 常 数 ) f(x,y)=d(常数) f(x,y)=d(常数) 相切时取得极值,此时俩曲线在切点处的法向量即 梯度向量(方向导数取最大值时的 l l l 方向,二维向量) 平行(此时梯度可能不相等)

2019.2.5 17:53
线性代数基础
矩阵与行列式的区别
矩阵类型
矩阵操作
矩阵数乘
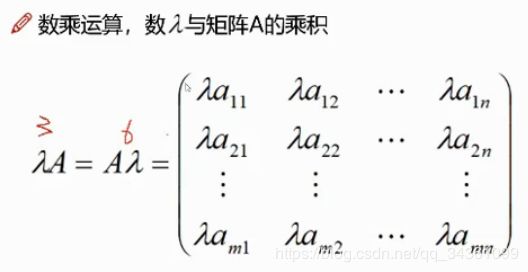
矩阵乘法
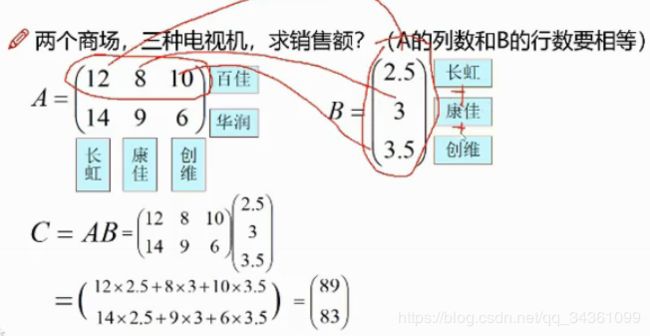
矩阵结合律
( A B ) C = A ( B C ) (AB)C = A(BC) (AB)C=A(BC)
λ ( A B ) = ( λ A ) B = A ( λ B ) \lambda (AB)=(\lambda A)B=A(\lambda B) λ(AB)=(λA)B=A(λB)
矩阵分配律
A ( B + C ) = A B + A C A(B+C)=AB+AC A(B+C)=AB+AC
( B + C ) A = B A + C A (B+C)A=BA+CA (B+C)A=BA+CA
矩阵的秩
指的矩阵的各行向量的极大线性无关组数即相互不平行的行向量数
零向量可看作与任何向量平行
矩阵的行秩=列秩
eg. 矩阵只需秩序为3
向量的内积
对应位置相乘后求和

内积的几何意义
物理背景下力做的功
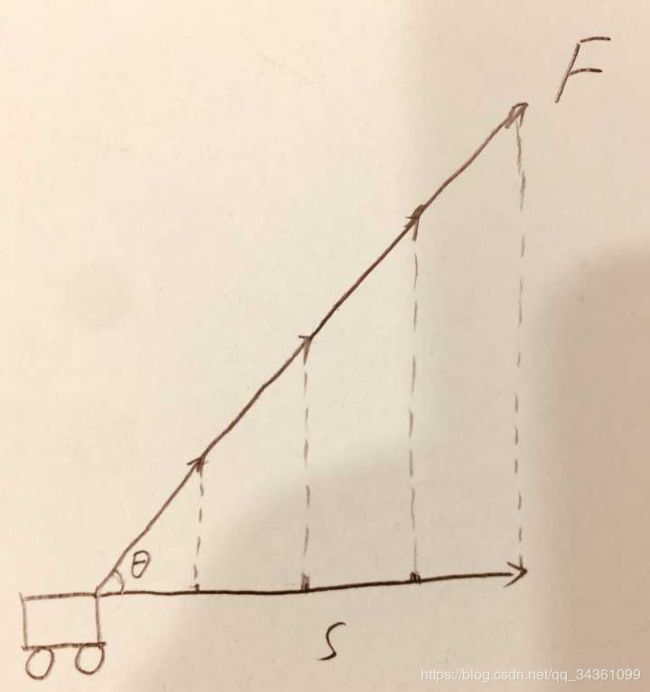
![]() 图片来源
图片来源
向量的长度
向量的正交
向量正交 ⇔ 垂直 ⇔ 内积为零
2019.2.6 14:16