前缀树的实现及应用
文章目录
- 一、前缀树
- 1. 概念
- 2. 应用
- 二、基于哈希表的实现及应用
- 1. 基于哈希表来实现
- 1.1 代码
- 1.2 优势
- 1.3 应用:[LintCode634. Word Squares](https://www.lintcode.com/problem/word-squares/description)
- 1.3.1 题意
- 1.3.2 暴力的思路
- 1.3.2 剪枝的思路
- 1.3.3 代码
- 三、基于树型结构的实现及应用
- 1. TrieNode
- 2. Trie
- 2.1 代码
- 3. [LeetCode 211. Add and Search Word - Data structure design](https://leetcode.com/problems/add-and-search-word-data-structure-design/)
- 4. [LeetCode 212. Word Search II](https://leetcode.com/problems/word-search-ii/)
一、前缀树
1. 概念
前缀树是一种数据结构,常用来处理字符串/单词。数据结构的本质是集合加操作,所以我们首先需要知道前缀树可以提供哪些操作。
- 增加:给定字符串,将其添加到前缀树中
- 判断给定前缀是否存在:给定任意字符串,返回该前缀树中当前是否存在以该字符串为前缀的单词
- 判断给定单词是否存在:给定单词,返回该前缀树中当前是否存在该单词
上面是前缀树必须满足的操作,但是在实际的一些题目中,还需要前缀树满足下面的:
- 返回给定前缀对应的所有单词:给定前缀,返回所有单词
2. 应用
- 前缀树最常见的应用是利用前缀查询和单词查询在
字符串搜索类题目中进行剪枝操作
二、基于哈希表的实现及应用
此节结合一道具体的LeetCode题目进行说明:208. Implement Trie (Prefix Tree)
1. 基于哈希表来实现
基于哈希表的实现非常的简单和直观
-
key:就是前缀 -
value: 就是每个前缀对应的单词 -
添加操作的时候,遍历给定的字符串的所有可能的前缀,分别建立
前缀到字符串的map
例如,给定字符串area,那么在建立前缀树的过程就是这样:a—>areaar---->areaare—>areaarea—>area
-
所以这种方式的空间复杂度非常的高,因为在具有相同的前缀字符串之间没有建立起有效的联系
还有一个重要的问题是,如果表示前缀树的根节点呢?
- 这里我们使用
""一个空字符串表示根节点,它对应的value就是所有的给定的字符串。
下面我们看具体的代码实现:
1.1 代码
class Trie {
Map<String,Set<String>> pre_to_word;
/** Initialize your data structure here. */
public Trie() {
pre_to_word = new HashMap<>();
pre_to_word.put("", new HashSet<>());
}
/** Inserts a word into the trie. */
public void insert(String word) {
//0. 遍历所有可能的前缀
for (int i = 0; i < word.length(); i++) {
String pre = word.substring(0, i+1);
//1. 判断该前缀是否已经存在
if (!pre_to_word.containsKey(pre)){
pre_to_word.put(pre, new HashSet<>());
}
pre_to_word.get(pre).add(word);
}
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
if (!pre_to_word.containsKey(word)){
return false;
}
return pre_to_word.get(word).contains(word);
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
return pre_to_word.containsKey(prefix);
}
}
1.2 优势
- 可以非常方便的返回前缀对应的所有单词
1.3 应用:LintCode634. Word Squares
1.3.1 题意
给定一些不重复单词,然后要找到一种或多种单词的排列顺序,构成一个单词矩阵,这些顺序满足每一行和每一列读出来的单词相同
例如:给定单词["ball","area","lead","lady"],它对应的一种合法的矩阵排列顺序如下:
可以看到,第i行和第i列的单词是相同的
- 每个单词的长度相同
长度相同其实就已经决定了这个单词矩阵一定是n*n的
1.3.2 暴力的思路
一种很容易的想法就是枚举所有可能的单词的排列的顺序,得到所有可能的单词矩阵,然后逐一筛选出合法的单词矩阵即可
继续思考一下,这种方式的时间复杂度呢
- 假设有
n个单词,每个单词长度为m,那么要构成m*m的单词矩阵,总共可能的单词矩阵的个数是多少呢? - 首先,我们肯定要从
n个单词中选出m个嘛,这里有多少种选则呢?利用排列组合的基础知识可以容易得到: C n m C_n^m Cnm - 现在选出了
m个单词,要按照一定的顺序摆放在m行上,这里又有多少种可能呢?同样根据排列组合的基础知识,这里是: m ! m! m!
m个行,m个单词
第1行,有m种可能
第2行,有m-1种可能
…
所以总的时间复杂度是: C n m m ! C_n^m m! Cnmm!
- 这个复杂度可以说是非常高的了
其实根据题目的要求,我们不需要在枚举出每一种可能之后,再去判断合法性,而是可以利用合法性在枚举的过程种,就把一些肯定不合法的策略晒出掉,这就是剪枝的思路
在DFS中,剪枝是非常重要的减少搜索空间的手段.
1.3.2 剪枝的思路
我们重新回顾整个思路,假设我们手上有一些单词,每个单词长度为m我们要选出一种摆放的顺序,形成一个单词矩阵,让其合法。
假设我们手上的单词就是:["ball","area","lead","lady"],现在我们按行逐行来思考。
- 第
0行:- 假设我们现在正在决定为第
0行摆放哪一个单词,很显然给定的所有的单词都可能放在第0行 - 所以,第
0行的时候,需要遍历所有的单词,让每一个单词都在第0行放置进行尝试 - 假设我们现在选择了
ball放置在第0行
- 假设我们现在正在决定为第
- 第
1行- 现在我们知道第
0行存放了ball,现在来决策第1行该放置哪个单词 - 因为题目要求第i行和第i列的单词相等,那么第一行的单词的首字母一定要是
a才满足条件 - 那么我第
1行的搜索空间就不是剩下的所有单词了,而是剩下的单词中以a为开头字母的单词。 - 那么如何才能找到以字母
a开头的所有可能的单词呢?。这里如果我们知道有前缀树这样的数据结构,就可以解决这个问题 - 所以,我们可以通过前缀树找到以字母
a开头的所有的单词,然后作为第1行放置单词的搜索空间,然后遍历这个空间中的每一个单词即可。到这里完成了第一层的剪枝 - 我们继续往下看,此时找到了以
a开头的所有单词:"area" - 假设现在第
1层放置的是单词area - 前
2层放置的单词分别是: ballarea- 这里可以继续利用题目规则,做后续的进一步的剪枝,现在第
1层放置了area,那么这个area到底是否合法呢? - 我们这里竖着看,如果
area合法,那么在剩下的单词中就一定存在前缀为:le和la的单词。如果不存在,说明area不合法,那么就在当前的搜索空间中尝试下一个单词,如果所有的单词都尝试了,还是不合法,那么就回到上一层。 - 这里是第二层剪枝
- 到这里整个题目的思路就霍然开朗了
- 现在我们知道第
其实到这里有一个非常重要的观察,第
i层的决策,是受到第0到第i-1层决策的影响的,这里的这个问题,让我想到了N皇后问题,也是同样的特性,第i层皇后放置的合法性受到前i层的影响,同样利用这个点去做剪枝。
1.3.3 代码
class LintCode634 {
class Trie {
Map<String, Set<String>> pre_to_word;
/** Initialize your data structure here. */
public Trie() {
pre_to_word = new HashMap<>();
pre_to_word.put("", new HashSet<>());
}
/** Inserts a word into the trie. */
public void insert(String word) {
pre_to_word.get("").add(word);
//0. 遍历所有可能的前缀
for (int i = 0; i < word.length(); i++) {
String pre = word.substring(0, i+1);
//1. 判断该前缀是否已经存在
if (!pre_to_word.containsKey(pre)){
pre_to_word.put(pre, new HashSet<>());
}
pre_to_word.get(pre).add(word);
}
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
if (!pre_to_word.containsKey(word)){
return false;
}
return pre_to_word.get(word).contains(word);
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
return pre_to_word.containsKey(prefix);
}
public Set<String> getAllWords(String pre){
return pre_to_word.get(pre);
}
}
List<List<String>> res = new ArrayList<>();
List<String> item = new ArrayList<>();
int wordLen = 0;
Trie preTree = new Trie();
public List<List<String>> wordSquares(String[] words) {
if (words == null || words.length == 0){
return res;
}
wordLen = words[0].length();
//0. 建立前缀树
for (String word : words) {
preTree.insert(word);
}
//1.
int l = 0;
dfs(l);
return res;
}
//0. 为第l层进行决策
private void dfs(int l) {
if (l == wordLen){
res.add(new ArrayList<>(item));
return;
}
//1. 为当前第l层进行决策,那么需要知道当前第l层放置的单词 以什么开头
// 当 l = 0,说明所有的单词都可以,pre = ""
// 当 l = 1, 假设l=0放置的单词是 ball
// 那么这一层放置的单词的开头应该是 a 那么这里的关系应该就是 item.get(i).charAt(l)
// i = 0 - (l-1)
String pre = "";
for (int i = 0; i < l; i++) {
pre += item.get(i).charAt(l);
}
//1.1 利用前缀树,获取前缀pre对应的所有单词,作为当前第l层的搜索空间
Set<String> allWords = preTree.getAllWords(pre);
//1.2 遍历所有的单词
for (String nextWord : allWords) {
//2. 第二层剪枝,判断第l层放置word是否合法
if (!checkValid(nextWord,l)){
continue;
}
//2.1 说明当前word合法
item.add(nextWord);
dfs(l+1);
item.remove(item.size() - 1);
}
}
private boolean checkValid(String nextWord, int l) {
//0. 假设现在l = 1
// 放置的单词为
// ball
// area
// 现在需要判断剩下的单词中是否存在 le la
// 那么首先需要把 le 和 la找出来
//1. 先完成已经放置单词的第 l+1列 到 wordLen-1列的添加
//1.1 最外层按列遍历
for (int i = l+1; i < wordLen; i++) {
String pre = "";
//1.2 然后遍历从第 0 - l-1层的 的i列
for (int j = 0; j < item.size(); j++) {
pre = pre + item.get(j).charAt(i);
}
//1.3 然后添加当前单词的第i列
pre += nextWord.charAt(i);
//1.4 然后判断此前缀是否存在
if (!preTree.startsWith(pre)){
return false;
}
}
return true;
}
}
- 代码看着挺多的,但是思路理解清楚了,其实也是不难写出来的
三、基于树型结构的实现及应用
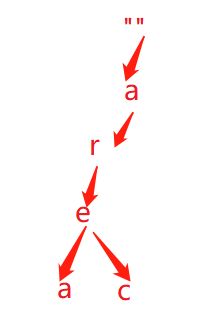
前面哈希表的实现有较高的空间复杂度,是因为多个相同的前缀重复的成为了一个key。而利用树型结构就不会存在这个问题,例如:给定单词area,arec,利用树型结构,会构成如下的形状:
1. TrieNode
首先需要定义一个前缀树节点
前缀树节点应当包含如下属性:
c:当前字符Map:当前节点的孩子节点们isWord:标记以当前字符结尾的字符是否为一个完整的单词s:当前节点结尾的字符对应的单词
class TrieNode {
char c;
Map<Character, TrieNode> children = new HashMap<>();
boolean isWord = false;
String s;
TrieNode() {
}
TrieNode(char c) {
this.c = c;
}
}
2. Trie
此节结合一道具体的LeetCode题目进行说明:208. Implement Trie (Prefix Tree)
2.1 代码
class Trie {
private TrieNode root;
/**
* Initialize your data structure here.
*/
public Trie() {
this.root = new TrieNode();
}
/**
* Inserts a word into the trie.
*/
public void insert(String word) {
//0. 获取根节点
TrieNode curNode = root;
//2. 遍历word,逐一添加
for (int i = 0; i < word.length(); i++) {
//1. 获取根节点的孩子
Map<Character, TrieNode> curChild = curNode.children;
char curChar = word.charAt(i);
//2.1 如果当前字符已经在字典树中了,则更新
if (curChild.containsKey(curChar)) {
curNode = curChild.get(curChar);
} else {
//2.2 如果不存在,则添加
TrieNode newNode = new TrieNode(curChar);
curChild.put(curChar, newNode);
curNode = newNode;
}
if (i == word.length() - 1) {
curNode.isWord = true;
curNode.s = word;
}
}
}
/**
* Returns if the word is in the trie.
*/
public boolean search(String word) {
if (strEndWith(word) == null) {
return false;
}
return strEndWith(word).isWord;
}
/**
* Returns if there is any word in the trie that starts with the given prefix.
*/
public boolean startsWith(String prefix) {
if (strEndWith(prefix) == null) {
return false;
} else {
return true;
}
}
public TrieNode strEndWith(String str) {
TrieNode curNode = root;
for (int i = 0; i < str.length(); i++) {
Map<Character, TrieNode> curChild = curNode.children;
char curChar = str.charAt(i);
if (!curChild.containsKey(curChar)) {
return null;
} else {
curNode = curChild.get(curChar);
}
}
return curNode;
}
}
3. LeetCode 211. Add and Search Word - Data structure design
- 本质上还是在前缀树的本身的实现
- 注意带有
.这种通配符的搜索即可
class LeetCode211_20200601{
class TrieNode {
char c;
Map<Character, TrieNode> children = new HashMap<>();
boolean isWord = false;
String s;
TrieNode() {
}
TrieNode(char c) {
this.c = c;
}
}
class WordDictionary {
private TrieNode root;
/** Initialize your data structure here. */
public WordDictionary() {
this.root = new TrieNode();
}
/** Adds a word into the data structure. */
public void addWord(String word) {
TrieNode curNode = root;
//2. 遍历word,逐一添加
for (int i = 0; i < word.length(); i++) {
//1. 获取根节点的孩子
Map<Character, TrieNode> curChild = curNode.children;
char curChar = word.charAt(i);
//2.1 如果当前字符已经在字典树中了,则更新
if (curChild.containsKey(curChar)) {
curNode = curChild.get(curChar);
} else {
//2.2 如果不存在,则添加
TrieNode newNode = new TrieNode(curChar);
curChild.put(curChar, newNode);
curNode = newNode;
}
if (i == word.length() - 1) {
curNode.isWord = true;
curNode.s = word;
}
}
}
public boolean search(String word) {
//0. 肯定需要对word遍历搜索每一个字符
// 那么需要一个startIndex
// 因为是在前缀树种搜索,所以在前缀树种搜索也需要一个起点,那就是root
int startIndex = 0;
TrieNode node = root;
return dfs(word,startIndex,node);
}
private boolean dfs(String word, int startIndex, TrieNode node) {
//0. 出口
if (startIndex == word.length()){
return node.isWord;
}
//1. 获取当前字符,和当前node的孩子节点
char curChar = word.charAt(startIndex);
Map<Character, TrieNode> curChildren = node.children;
//2. 判断当前字符是否为 '.'
if (curChar != '.'){
//2.1 如果是普通字符,则看该字符是否存在于当前的孩子节点中
if (!curChildren.containsKey(curChar)){
return false;
}
return dfs(word, startIndex+1, curChildren.get(curChar));
}else {
//2.2 如果当前字符是 '.', 那么需要遍历当前所有的孩子节点
Set<Character> set = curChildren.keySet();
//2.3 遍历set,只要有一个字符满足条件,则可以
for (Character cur_char:set){
if (dfs(word, startIndex + 1, curChildren.get(cur_char))){
return true;
}
}
//2.4 如果所有的都不满足,则返回false
return false;
}
//3. 如果不是上述两种字符,返回false
}
}
}
4. LeetCode 212. Word Search II
- 给定一个二维的字符矩阵
- 给定一个字符串数组
- 搜索在二维字符矩阵中出现过的字符
/*
0. 将给定的words中的所有单词新建为一颗前缀树
1. 搜索board,也是同样的需要遍历,每一个为起点,起点的合法性也有前缀树来判断
2. 然后以位置为起点在board中进行dfs,遇到node对应的isWord为true,就记录,然后继续
3. 继续找到新的起点,看是否存在其他的单词
*/
class LeetCode212 {
class TrieNode {
char c;
Map<Character, TrieNode> children = new HashMap<>();
boolean isWord = false;
String s;
TrieNode() {
}
TrieNode(char c) {
this.c = c;
}
}
class Trie {
private TrieNode root;
/**
* Initialize your data structure here.
*/
public Trie() {
this.root = new TrieNode();
}
/**
* Inserts a word into the trie.
*/
public void insert(String word) {
//0. 获取根节点
TrieNode curNode = root;
//2. 遍历word,逐一添加
for (int i = 0; i < word.length(); i++) {
//1. 获取根节点的孩子
Map<Character, TrieNode> curChild = curNode.children;
char curChar = word.charAt(i);
//2.1 如果当前字符已经在字典树中了,则更新
if (curChild.containsKey(curChar)) {
curNode = curChild.get(curChar);
} else {
//2.2 如果不存在,则添加
TrieNode newNode = new TrieNode(curChar);
curChild.put(curChar, newNode);
curNode = newNode;
}
if (i == word.length() - 1) {
curNode.isWord = true;
curNode.s = word;
}
}
}
/**
* Returns if the word is in the trie.
*/
public boolean search(String word) {
if (strEndWith(word) == null) {
return false;
}
return strEndWith(word).isWord;
}
/**
* Returns if there is any word in the trie that starts with the given prefix.
*/
public boolean startsWith(String prefix) {
if (strEndWith(prefix) == null) {
return false;
} else {
return true;
}
}
public TrieNode strEndWith(String str) {
TrieNode curNode = root;
for (int i = 0; i < str.length(); i++) {
Map<Character, TrieNode> curChild = curNode.children;
char curChar = str.charAt(i);
if (!curChild.containsKey(curChar)) {
return null;
} else {
curNode = curChild.get(curChar);
}
}
return curNode;
}
}
//0. 全局变量
List<String> ans = new ArrayList<>();
int[] dx = {1,-1,0,0};
int[] dy = {0,0,1,-1};
public List<String> findWords(char[][] board, String[] words) {
if (board == null || board.length == 0){
return ans;
}
if (words == null || words.length == 0){
return ans;
}
//0. 遍历words建立前缀树
Trie preTree = new Trie();
for (String word : words) {
preTree.insert(word);
}
//1. 遍历board找到合法的起点
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
//1.1 如果当前前缀树中存在以当前字符为前缀的单词
if (preTree.startsWith("" + board[i][j])){
//1.2 那么就以这个点为起点进行遍历
// board i j 起点 当前的item 当前的前缀树的起点
// 访问标记
boolean[][] vis = new boolean[board.length][board[0].length];
vis[i][j] = true;
TrieNode curNode = preTree.root.children.get(board[i][j]);
String item = "" + board[i][j];
dfs(board,i,j,item,vis,curNode);
}
}
}
return ans;
}
private void dfs(char[][] board, int i, int j, String item, boolean[][] vis, TrieNode curNode) {
//0. 出口
//0.1 这里一定要注意!!!这里不一定就要返回
//0.2 因为这里完全可以出现什么呢?完全可以出现 比如 aaa aaab这两种情况
if (curNode.isWord){
if (!ans.contains(curNode.s)){
ans.add(curNode.s);
}
}
//1. i,j是起点,向4个方向做dfs
for (int k = 0; k < 4; k++) {
int nx = i + dx[k];
int ny = j + dy[k];
if (nx < 0 || nx >= board.length || ny < 0 || ny >= board[0].length){
continue;
}
if (vis[nx][ny]){
continue;
}
if (curNode.children.containsKey(board[nx][ny])){
vis[nx][ny] = true;
dfs(board, nx, ny, item, vis, curNode.children.get(board[nx][ny]));
vis[nx][ny] = false;
}
}
}
}