【算法应用】Thompson Sampling--汤普森采样应用之代码篇 （Python）

Thompson Sampling–汤普森采样应用之代码篇

关键词：机器学习，在线学习，人工智能，强化学习，汤普森采样解决最优路径问题，汤普森采样代码例子，Thompson Sampling 机器学习代码例子

1.简介

汤普森选样是一种采样方法，其意在研究在探索成本最低的情况下找到最高的收益（Global Maximum）。如果你还不清楚基础概念，可以看这一篇：

【算法】如何根据算法在赌场发家致富？汤普森采样之多臂强盗算法！

汤普森采样的应用前景其实非常非常的广，小到出门上班选择路线，大到赌场梭哈发家致富。

而当前比较流行的研究应用有：
1）多臂强盗问题（Multi-armed bandit）也就是我们说的赌场老虎机；
2）EE问题（Exploration-Exploitation），也就是大家说的冷启动问题，旨在研究提高给用户推送广告的准确性；
3）机器学习-强化学习（reinforcement learning），人工智能，都很厉害，但是目前看以看到的研究材料不多。
。。。以及非常非常多，万物皆可汤普森。
这里为了引发大家的思路写一个很简单很basic的应用场景。

2.应用举例

2.1故事背景

我们的赌吧老哥Tom刚刚搬到一个新城市，安顿好住所之后嘛，赌瘾来犯难免手痒，他就想了解一下当地赌场的情况。

对于Tom老哥而言最首要的问题就是交通问题，在这个新城市有很多种到达赌场的路线，我们假设他知道每条路大概消耗的时间而不知道每条路平均的消耗时间。（也就是说他知道这条路距离比较长，但是这条路他不堵车啊，反而到达时间要比别的短）。因此他要做的第一件事就是找到到达赌场平均时间最短的那一条路径。

2.2信息分析

假设我们有如下的线路地图，其中有V1到V12一共12个vertex，以及16条路径。Tom老哥的家在V1，赌场的位置在V12。

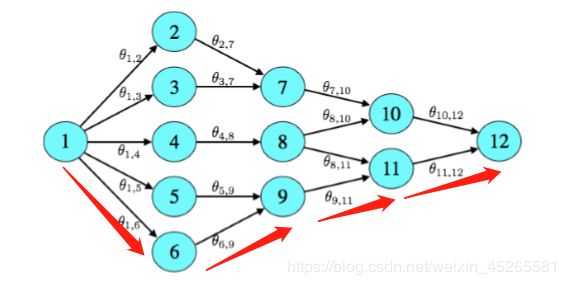
我们通过注视法可以看出来其实从V1到V12一共只有6条路可以走，设为X1，X2,…,X6。

2.3设置事件属性

因为我们目前要处理的是随机时间，所以我们给Xi定义不同的六种随机属性，然后写一个随机时间模拟器，用来模拟每条路每次的耗时情况。
这里我们模拟器输入为每条路的属性，模拟器会首先提取出该条路段的最高限速，用模拟的概率表示突发时间，如果有突发事件发生速度会有不同比例的减低。
代码不需要看懂，明白意思就行！
我这边是定义了一个x的属性，为了方便修改直接用了list而没有创建类，在比较大的项目中我真的强烈建议大家用类来做，list修改起来会瞎真的。

#每条路属性定义
 #x=[limited speed, s:km, probability that may rain or tafic jam]
    x1=[30,15,10,"x1",0,1,1]
    x2=[40,10,5,"x2",0,1,1]
    x3=[60,30,30,"x3",0,1,1]
    x4=[40,30,30,"x4",0,1,1]
    x5=[55,27,40,"x5",0,1,1]
    x6=[60,30,50,"x6",0,1,1]
#随机事件模拟器
def trafic_monitor_1(x):
    rain_prob=random.randint(1, 100)
    trafic_jam_prob = random.randint(1, 100)
    simple_prob=[i for i in range(1,x[2])]
    v=x[0]
    if rain_prob in simple_prob:
        print("it's raining")
        v=v*0.85
    else:print("it's not raining")
    if trafic_jam_prob in simple_prob:
        print("it's a trafic jam")
        v=v*0.75
    else:print("there is no trafic jam")

    return x[1]/v

2.4建立beta模型

我们要为每一个选线建一个独立的beta模型，这个的确一行代码就可以。

x1[4]=beta.rvs(x1[5],x1[6])
        x2[4] = beta.rvs(x2[5], x2[6])
        x3[4] = beta.rvs(x3[5], x3[6])
        x4[4] = beta.rvs(x4[5], x4[6])
        x5[4] = beta.rvs(x5[5], x5[6])
        x6[4] = beta.rvs(x6[5], x6[6])

2.5完成汤普森采样模型

随机事件模拟器和beta坐标都有了，现在我们只需要设定一个可以更新模型的机制再让他循环起来就可以了。这里我们简单的把他看作一个Bernoulli问题，也就是说我们要设定一个时间区间（奖惩区间），只要你够快进入到这个时间区间，我就算你成功，就会获得对应的奖励S+=1，如果模拟的时间结果很慢，没有进入到我们所设定的区间，那么就会被判定为失败，相应的获得惩罚F+=1。
这里我们设定完成时间在45分钟(0.75h)就算成功，反之则失败。

if time_i <= 0.75:
    list_xi[max_index[0]][5]+=1
else:
    list_xi[max_index[0]][6]+= 1

简单吧，当然如果你不满足于做一个Bernoulli人，你可以对他的奖惩机制做任何你觉得合理的改变。比如细分他的奖励区间，或者用更直观的对应奖励方式，比如胜利后S+=log(reward)，失败后F+=1/reward。具体怎么修改要根据你的reward。

3.开始模拟

为了体现出模拟过程，我把每个路径Xi的beta坐标拆出来给你们看。

3.1第一轮

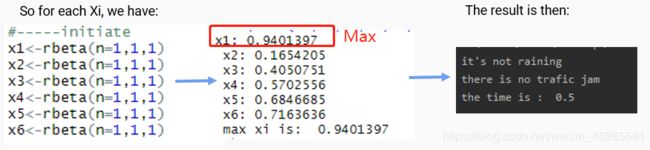
我们可以看到第一次X1有最大的贝塔值，所以我们选择路径X1并且获得了对应的结果：0.5h < 0.75h。X1成功了，我们给他对应的奖励S+=1。

3.2第二轮

这一次X2给出了最大的贝塔值，这也体现了Thompson不greedy的特性。但是X2的结果超出了我们的区间，所以X2获得惩罚F+=1.

3.3第三轮

X4被选择，其结果也超出了我们给定的区间，获得惩罚F+=1.

3.4结果

我们直接让他自己运行1000次

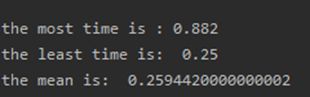
可以看到他已经把mean压到了0.259，那么怎么看该算法的好坏呢？我们先介绍一个衡量标准，regret值，也就是后悔值。在我们的Bernoulli问题中，我们可以定义其为
$$regre{t}_t(\theta )=ma{x}_i{\theta }_i-{\theta }_{xt}$$
t：代表时间段，也就是循环的第几次
i：用的哪一种方法
这个公式说人话就是看你每一次模拟得到的reward和我们目前得到最好的reward比要差多少。差的越多你当然越后悔，后悔指数也就越高。

这里我们直接用matplotlib里的plot工具把他画出来。

#准备坐标
x=[i for i in range(1,1001)]
y2=[i for i in range(1,1001)]
#画图
plt.plot(x,list_record_regret,lw=2,label="regrets curve")
plt.legend()
plt.show()

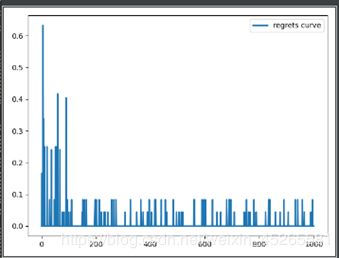
从图中我们可以看到大约100次以后我们的后悔值就缩小到一个比较小的区间，之后一直在一个较小的区间震荡。震荡的可能原因有：1）奖惩机制分配不够细腻，我们直接定义了大于45分钟就减一，小于45分钟就加一。那么我们遇到10分钟和40分钟的奖励情况是一样的都是加一，就不能很好的分隔开。假如我们设置奖罚机制更细腻，更和reward相关，得到的结果会更好；2）因为我们应用的体系为beta分布体系，所以即使已经找到最优方案，还是会有次优方案被选到的概率。并且汤普森采样旨在选取一个比较好的mean区间，如果和greedy算法相比较我们会发现汤普森的mean会更好。

4.小结

就目前来看，汤普森采样在人工智能线上学习有着无限的前景，其应用场景以及应用效率远非本文中的例子可以比拟的。本文的目的在于抛砖引玉，启发大家研究更多的汤普森采样的用法。

需要完整代码demo可以留言，有问题交流可以留言或私信。

Reference
1.D.J.Russo, B.V.Roy, A.Kazerouni, I.Osband and Z.Wen4 'A Tutorial on Thompson Sampling ’
url: https://web.stanford.edu/~bvr/pubs/TS_Tutorial.pdf