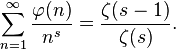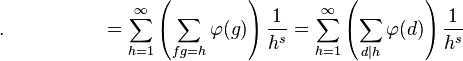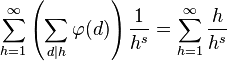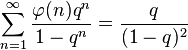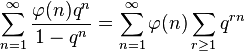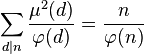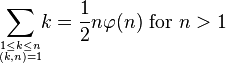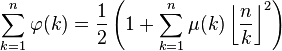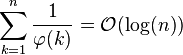欧拉函数
在数论中,对正整数n,欧拉函数![]() 是小于或等于n的正整数中与n 互质的数的数目。此函数以其首名研究者欧拉命名,它又称为φ函数(由高斯所命名)或是欧拉总计函数[1](totient function,由西尔维斯特所命名)。
是小于或等于n的正整数中与n 互质的数的数目。此函数以其首名研究者欧拉命名,它又称为φ函数(由高斯所命名)或是欧拉总计函数[1](totient function,由西尔维斯特所命名)。
例如![]() ,因为1,3,5,7均和8互质。
,因为1,3,5,7均和8互质。
欧拉函数实际上是模n的同余类所构成的乘法群(即环![]() 的所有单位元组成的乘法群)的阶。这个性质与拉格朗日定理一起构成了欧拉定理的证明。
的所有单位元组成的乘法群)的阶。这个性质与拉格朗日定理一起构成了欧拉定理的证明。
目录
- 历史:欧拉函数与费马小定理
- 欧拉函数的值
- 性质
- 生成函数
- 欧拉函数的走势
- 其他与欧拉函数有关的等式
- 与欧拉函数有关的不等式
- 参考来源
- 文献来源
历史:欧拉函数与费马小定理编辑
1736年,欧拉证明了费马小定理[2]:
-
假若
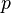 为质数,
为质数,
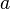 为任意正整数,那么
为任意正整数,那么
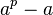 可被
可被
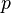 整除。
整除。
然后欧拉予以一般化:
-
假若
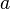 与
与 互质,那么
互质,那么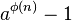 可被
可被 整除。亦即,
整除。亦即,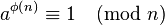 。
。
其中![]() 即为欧拉总计函数。如果
即为欧拉总计函数。如果![]() 为质数,那么
为质数,那么![]() ,因此,有高斯的版本[3]:
,因此,有高斯的版本[3]:
-
假若
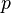 为质数,
为质数,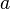 与
与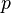 互质(
互质(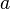 不是
不是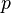 的倍数),那么
的倍数),那么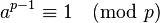 。
。
欧拉函数的值编辑
![]() (小于等于1的正整数中唯一和1互质的数就是1本身)。
(小于等于1的正整数中唯一和1互质的数就是1本身)。
若n是质数p的k次幂,![]() ,因为除了p的倍数外,其他数都跟n互质。
,因为除了p的倍数外,其他数都跟n互质。
欧拉函数是积性函数,即是说若m , n互质,![]() 。证明:设A , B , C是跟m , n , mn互质的数的集,据中国剩余定理,
。证明:设A , B , C是跟m , n , mn互质的数的集,据中国剩余定理,![]() 和
和![]() 可建立双射 (一一对应)的关系。(或者也可以从初等代数角度给出欧拉函数积性的简单证明)因此
可建立双射 (一一对应)的关系。(或者也可以从初等代数角度给出欧拉函数积性的简单证明)因此![]() 的值使用算术基本定理便知,
的值使用算术基本定理便知,
-
若
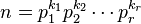
-
则
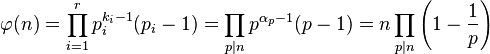 。
。
其中![]() 是使得
是使得![]() 整除
整除![]() 的最大整数
的最大整数![]() (这里
(这里![]() )。
)。
例如![]()
性质编辑
n的欧拉函数![]() 也是循环群 C n的生成元的个数(也是n阶分圆多项式的次数)。C n中每个元素都能生成C n的一个子群,即必然是某个子群的生成元。而且按照定义,不同的子群不可能有相同的生成元。此外,C n的所有子群都具有C d的形式,其中d整除n(记作d | n)。因此只要考察n的所有因数d,将C d的生成元个数相加,就将得到C n的元素总个数:n。也就是说:
也是循环群 C n的生成元的个数(也是n阶分圆多项式的次数)。C n中每个元素都能生成C n的一个子群,即必然是某个子群的生成元。而且按照定义,不同的子群不可能有相同的生成元。此外,C n的所有子群都具有C d的形式,其中d整除n(记作d | n)。因此只要考察n的所有因数d,将C d的生成元个数相加,就将得到C n的元素总个数:n。也就是说:
其中的d为n的正约数。
运用默比乌斯反转公式来“翻转”这个和,就可以得到另一个关于![]() 的公式:
的公式:
其中μ是所谓的默比乌斯函数,定义在正整数上。
对任何两个互质的正整数a , m(即gcd( a , m ) = 1),![]() ,有
,有
即欧拉定理。
这个定理可以由群论中的拉格朗日定理得出,因为任意与m互质的a都属于环![]() 的单位元组成的乘法群
的单位元组成的乘法群![]()
当m是质数p时,此式则为:
即费马小定理。
生成函数编辑
由![]() ( n )生成的狄利克雷级数是:
( n )生成的狄利克雷级数是:
其中ζ( s )是黎曼ζ函数。推导过程如下:
欧拉函数生成的朗贝级数如下:
其对于满足| q |<1的q 收敛。
推导如下:
后者等价于:
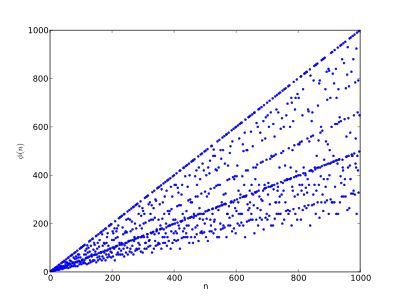
欧拉函数的走势编辑
随着n变大,估计![]() 的值是一件很难的事。当n为质数时,
的值是一件很难的事。当n为质数时,![]() ,但有时
,但有时![]() 又与n差得很远。
又与n差得很远。
在n足够大时,有估计:
-
对每个ε > 0,都有
n >
N (ε)使得
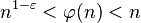
如果考虑比值:
由以上已经提到的公式,可以得到其值等于类似![]() 的项的乘积。因此,使比值小的n将是两两不同的质数的乘积。由素数定理可以知道,常数ε可以被替换为:
的项的乘积。因此,使比值小的n将是两两不同的质数的乘积。由素数定理可以知道,常数ε可以被替换为:
![]() 就平均值的意义上来说是与n很相近的,因为:
就平均值的意义上来说是与n很相近的,因为:
其中的O表示大O符号。这个等式也可以说明在集合 {1, 2, ..., n }中随机选取两个数,则当n趋于无穷大时,它们互质的概率趋于![]() 。一个相关的结果是比值
。一个相关的结果是比值![]() 的平均值:
的平均值:
其他与欧拉函数有关的等式编辑
与欧拉函数有关的不等式编辑
参考来源编辑
- Milton Abramowitz、Irene A. Stegun,Handbook of Mathematical Functions, (1964) Dover Publications , New York. ISBN 0-486-61272-4 . 24.3.2节.
- Eric Bach、Jeffrey Shallit,Algorithmic Number Theory ,卷1, 1996, MIT Press. ISBN 0-262-02405-5 , 8.8节,234页.
- Kevin Ford, The number of solutions of φ(x)=m, Ann. of Math. 150(1999), 283--311.
- 柯召,孙琦:数论讲义(上册),第二版,高等教育出版社,2001
文献来源编辑
- ^ Where does the word “totient” come from?
- ^ Mathematical Thought From Ancient to Modern Times,第2卷,p.608
- ^ Mathematical Thought From Ancient to Modern Times,第3卷,p.814