ICRA 2020——Dilated Point Convolutions: On the Receptive Field Size of Point Convolutions on 3D Point
Dilated Point Convolutions: On the Receptive Field Size of Point Convolutions on 3D Point Clouds
- Abstract
- （一）Introduction
- （二）Related Work
- （三）Approach
- （四）Experiments
- （五）Conclusion
论文：https://arxiv.org/abs/1907.12046
Abstract
- 提出了扩张点卷积（DPC）。
- 感受野的大小与3D点云处理任务的性能直接相关，包括语义分割和对象分类。
- DPC大大增加了点卷积的接收场大小。
- DPC可以轻松地集成到大多数现有的点卷积网络中。
（一）Introduction
重要性： 神经单元的感受野描述了影响其输出值的输入数据区域。感受野之外的所有输入数据均不影响输出。因此，大的感受野很重要，因为它们可以在较大的输入上下文中进行推理。
困难： 由于3D点云的结构不均匀，因此难以计算接收场的理论大小，因此该研究尤其具有挑战性。
分析： 可视化感受野以分析不同的网络体系结构，进行全面的消融研究，比较几种增加点卷积感受野的策略。
- 堆叠卷积层
- 使用较大内核
通过观察所得感受野的程度，注意到它们的影响仍然相当有限。
改进： 基于这些观察，论文提出了Dilated Point Convolutions作为一种显着增加点卷积的感受野大小的方法。
贡献:
- 评估了当前使用点卷积方法增加感受野的最常用策略。
- 可视化点卷积的感受野，以做出有根据的网络设计。
- 从这些观察结果中，提出膨胀点卷积（DPC）作为一种明显增加接收场大小的机制。
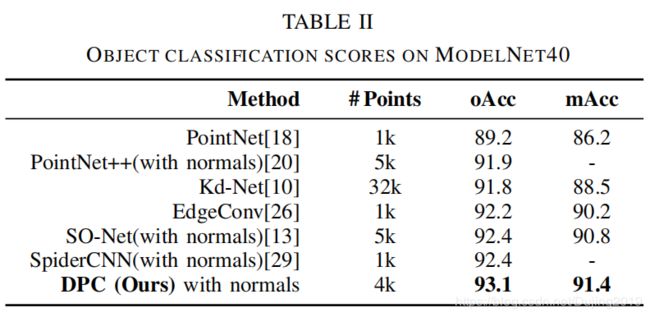
- 使用DPC，在S3DIS 和ScanNet 上的3D语义分割任务以及ModelNet40 上的形状分类上取得了非常好的结果。
（二）Related Work
大同小异，故不重复赘述。
（三）Approach
A. Point Convolutions
点卷积可以使用D维空间中连续卷积的一般定义来表述。连续卷积定义为:
( f ∗ g ) ( p i ) = ∫ − ∞ + ∞ f ( p j ) ⊙ g ( p i − p j ) d p j − − − − − ( 1 ) (f\ast g)(p_{i})=\int_{- \infty}^{+ \infty}f(p_{j})\odot g(p_{i}-p_{j})dp_{j}-----(1) (f∗g)(pi)=∫−∞+∞f(pj)⊙g(pi−pj)dpj−−−−−(1)
注释：
- ⊙ \odot ⊙ 是连续特征函数 f : R D → R F f:R^{D}\rightarrow R^{F} f:RD→RF的Hadamard-product ，为每个位置 p j ∈ R D p_{j}\in R^{D} pj∈RD分配一个特征向量 f ( p j ) ∈ R F f(p_{j})\in R^{F} f(pj)∈RF
- 连续核函数 g : R D → R F g:R^{D}\rightarrow R^{F} g:RD→RF将相对位置映射到核权重。
- 3D点云，D = 3，特征向量可以包含点位置，颜色和法线使得 f ( p ) ∈ R 9 f(p)\in R^{9} f(p)∈R9. 如图2.
在大多数实际应用中，例如在重建3D点云时，特征函数 f f f尚不完全清楚，因为只有有限数量的N个点位置 p n p_n pn被观察到，甚至被占据。使用蒙特卡洛积分，连续卷积可以近似为:
( f ∗ g ) ( p i ) ≈ 1 N ∑ n = 1 N f ( p n ) ⊙ g ( p i − p n ) − − − − − ( 2 ) (f\ast g)(p_{i})\approx \frac{1}{N}\sum_{n=1}^{N}f(p_{n})\odot g(p_{i}-p_{n})-----(2) (f∗g)(pi)≈N1n=1∑Nf(pn)⊙g(pi−pn)−−−−−(2)
基于多层感知器（MLP）将内核函数 g(·) 实现为学习的参数函数：
g ( p ; θ ) = M L P ( p ; θ ) − − − − − − − − − ( 3 ) g(p;\theta)= MLP(p;\theta)---------(3) g(p;θ)=MLP(p;θ)−−−−−−−−−(3)
注释：
- p是两点之间的相对位置，
- θ是一组学习的参数。
为了提取高频信号，重要的是定义局部核。在2D图像CNN中，这是通过3×3或5×5像素内核实现的。对于点卷积，可以通过限制局部内核支持的基数来实现此效果，即通过在每个点 p i p_i pi周围定义局部邻域 N i N_i Ni。
( f ∗ g ) ( p i ) ≈ 1 ∣ N i ∣ ∑ p k ∈ N i f ( p k ) ⊙ g ( p i − p k ) − − − − − ( 4 ) (f\ast g)(p_{i})\approx \frac{1}{\left | N_{i}\right |}\sum_{p_{k}\in N_{i}}f(p_{k})\odot g(p_{i}-p_{k})-----(4) (f∗g)(pi)≈∣Ni∣1pk∈Ni∑f(pk)⊙g(pi−pk)−−−−−(4)
目前很多方法都使用了连续卷积的上述定义。
B. Receptive Field Size.
增加接收场大小的常用方法:
- 堆叠多个（点）卷积层。 EdgeConvs 堆叠3个卷积层，SpiderCNN 使用4层，PCCN使用8层。论文比较3、5和7层。
- 增加卷积的内核大小。在点卷积的设置中，此效果是通过选择较大数量的k最近邻来实现的。但是注意，这不会增加模型参数的数量，因为使用参数内核函数g(·）在相对点位置上计算了内核权重。 这与在离散网格位置（例如2D图像CNN）上定义的卷积形成鲜明对比，在卷积中较大的内核会增加模型参数的数量。
Dilated Point Convolutions.
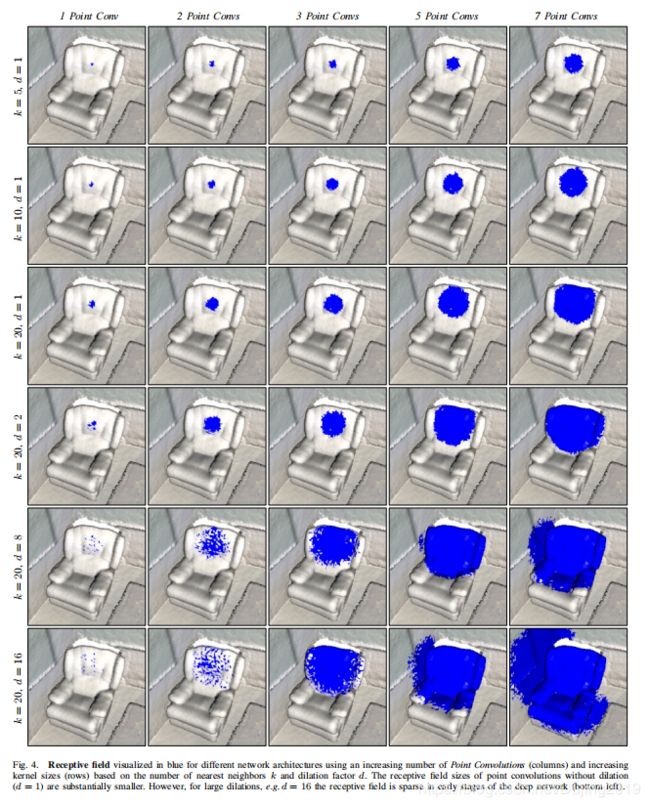
现状： 使用前面提到的方法，接收场大小仍然受到限制，如图4的前3行。
改进： 论文提出了扩张点卷积（DPC）作为增加接收场大小的一种有效机制。
细节：
DPCs等于点卷积（PC），但是它们在选择相邻点的方式上有所不同：虽然PC直接使用k个最近邻居，但DPC首先计算k·d个最近邻居，然后选择每个第d个邻居，见图2（右）。
注意，对于d = 1，DPC与PC相同。扩张会导致感受野的大小显着增加（见图4）。但是，参数的数量保持不变。需要计算的更大数量的k·d邻居增加了sublinear计算开销。见表IV。
如果本地内核邻域N来自最近邻搜索，则可以将DPC直接添加到现有的大多数卷积网络中，而只需进行最小的修改即可。
（四）Experiments
Model Architecture.
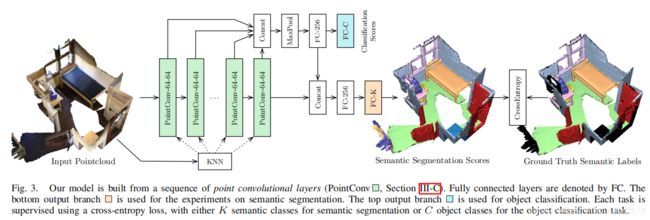
- 分支（以绿色显示）由堆叠的（膨胀的）点卷积组成。
- 动态计算每个点的k个最近邻居（KNN）。
- 最终点特征与通过在不同深度级别，对级联的点特征进行最大池化而获得的全局特征进行级联。
A. 3D Semantic Segmentation
通常，一旦感受野的大小超过训练物的大小，小的训练物就会阻碍网络从更大的环境中学习。点被采样而不替换，如果少于4092点，使用零填充。
B. 3D Object Classification
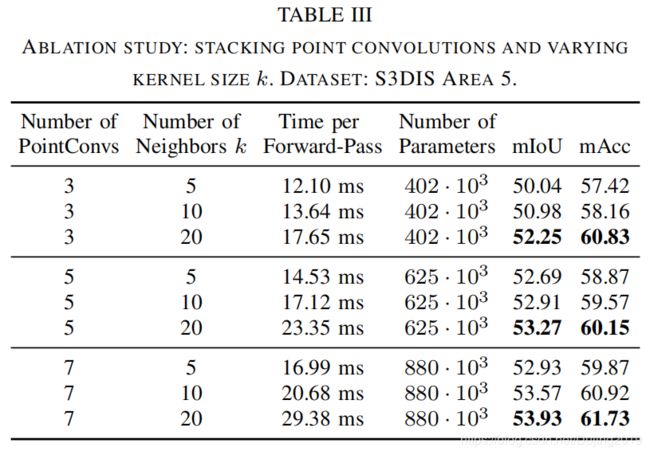
C. Ablation Study
主要分析超参数：点卷积层的数量，最近的邻居k和扩张因子d
Depth and Number of Neighbors k：
表释：
- 通过增加卷积层的数量，可以构建更深的网络。
- 与离散卷积相似，深点卷积网络的性能优于浅层卷积。
- 性能随着邻点数量的增加而提高。但是，增加邻点数会增加计算成本，从而导致推理时间变慢。
- 增加卷积数量会导致额外的内存消耗。
Dilation Factor d：
表释：
- Dilated Point Convolutions是快速增加卷积感受野的有效方式。
- 使用膨胀，在恒定的内存需求和处理时间的边际增加下，感受野可以显着增加。
- 语义分割任务的性能提高表明，更大的感受野很重要。
- 但是，快速增加的感受野会在后面的层中导致较大的感受野，这也是导致早期层中稀疏采样邻域的原因。这会使网络更难学习高频或局部特征。
Model Size：
由于内核函数 g( p) 是在相对点位置p上定义的，因此可训练参数的数量与邻点的数量k（因此与膨胀因子d）无关。这样，增加邻居数k（或膨胀因子dd）会增加感受野，而不会增加模型大小。
（五）Conclusion
- 回顾了几种增加3D点卷积的感受野大小的机制。
- 根据感受野大小分析和比较了不同的网络体系结构，发现它们与点卷积网络的性能直接相关。
- 提出dilated point convolutions以显着增加点卷积的接收场大小。
- 对3D语义分割和3D对象分类的基准方法有实质性改进。
- 扩张机制可以轻松地集成到大多数现有的点卷积网络中。