威佐夫博弈（ayit-609）

题目
有2堆石子。A B两个人轮流拿，A先拿。每次可以从一堆中取任意个或从2堆中取相同数量的石子，但不可不取。拿到最后1颗石子的人获胜。假设A B都非常聪明，拿石子的过程中不会出现失误。给出2堆石子的数量，问最后谁能赢得比赛。
例如：2堆石子分别为3颗和5颗。那么不论A怎样拿，B都有对应的方法拿到最后1颗。
Input
第1行：一个数T，表示后面用作输入测试的数的数量。（1 <= T <= 10000) 第2 - T + 1行：每行2个数分别是2堆石子的数量，中间用空格分隔。(1 <= N <= 2000000)
Output
共T行，如果A获胜输出A，如果B获胜输出B。
Sample Input
3
3 5
3 4
1 9
Sample Output
B
A
A
以下选址百度：
威佐夫博弈（Wythoff’s game）：有两堆各若干个物品，两个人轮流从某一堆取至少一个或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。
这种情况下是颇为复杂的。我们用（a[k]，b[k]）（a[k] ≤ b[k] ,k=0，1，2，…,n)表示两堆物品的数量并称其为局势，如果甲面对（0，0），那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势是：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）、（8，13）、（9，15）、（11，18）、（12，20）。（注：k表示奇异局势的序号， 第一个奇异局势k=0）
可以看出,a[0]=b[0]=0,a[k]是未在前面出现过的最小自然数,而 b[k]= a[k] + k。
奇异局势的性质编辑
1。任何自然数都包含在一个且仅有一个奇异局势中。
由于a[k]是未在前面出现过的最小自然数，所以有a[k] > a[k-1] ，而 b[k]= a[k] + k > a[k-1] + k > a[k-1] + k - 1 = b[k-1] > a[k-1] 。所以性质1成立。
2。任意操作都可将奇异局势变为非奇异局势。
事实上，若只改变奇异局势（a[k]，b[k]）的某一个分量，那么另一个分量不可能在其他奇异局势中，所以必然是非奇异局势。如果使（a[k]，b[k]）的两个分量同时减少，则由于其差不变，且不可能是其他奇异局势的差，因此也是非奇异局势。
3。采用适当的方法，可以将非奇异局势变为奇异局势。
假设面对的局势是（a,b），若 b = a，则同时从两堆中取走 a 个物体，就变为了奇异局势（0，0）；如果a = a[k] ，b > b[k] 那么，取走b - b[k]个物体，即变为奇异局势；如果 a = a[k] ， b < b[k] 则同时从两堆中拿走a-a[b-a]（注：这里b-a是a的下标， 不是a*(b-a)） 个物体变为奇异局势（ a[b-a], b-a+a[b-a]）；如果a > a[k] ，b= a[k] + k 则从第一堆中拿走多余的数量a - a[k] 即可；如果a < a[k] ，b= b[k],分两种情况，第一种，a=a[n] （n< k）从第二堆里面拿走 b - b[n] 即可；第二种，a=b[n] （n < k）从第二堆里面拿走 b - a[n] 即可。

证明过程编辑
方法一
简单分析一下，容易知道两堆石头地位是一样的，我们用余下的石子数(a,b)来表示状态，并画在平面直角坐标系上。
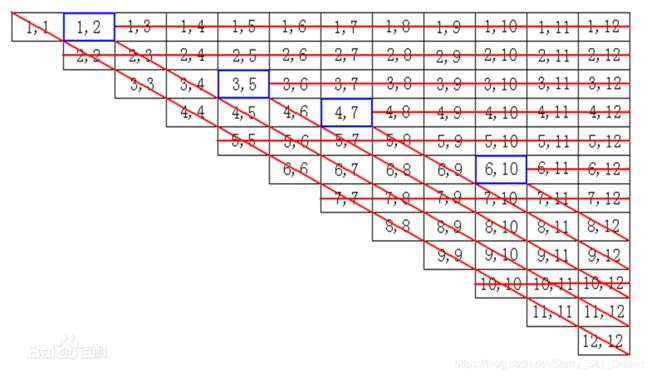
用之前的定理：有限个结点的无回路有向图有唯一的核 中所述的方法寻找必败态。先标出(0,0)，然后划去所有(0,k),(k,0),(k,k)的格点；然后找y=x上方未被划去的格点，标出(1,2)，然后划去(1,k),(k,2),(1+k,2+k)，同时标出对称点(2,1)，划去(2,k),(1,k),(2+k,1+k)；然后在未被划去的点中在y=x上方再找出(3,5)。。。按照这样的方法做下去，如果只列出a<=b的必败态的话，前面的一些是(0,0),(1,2),(3,5),(4,7),(6,10),…
接下来就是找规律的过程了，可能很辛苦，但是我写得也不容易，而且我暂时没有看到其他地方有这样的证明过程。
忽略(0,0)，记第n组必败态为(a[n],b[n])
命题一：a[n+1]=前n组必败态中未出现过的最小正整数
[分析]：如果a[n+1]不是未出现的数中最小的，那么可以从a[n+1]的状态走到一个使a[n+1]更小的状态，和我们的寻找方法矛盾。
命题二：b[n]=a[n]+n
[分析]：归纳法：若前k个必败态分别为(a[k],a[k]+k)，下证：第k+1个必败态为(a[k+1],a[k+1]+k+1)
从该第k+1个必败态出发，一共可能走向三类状态，从左边堆拿走一些，从右边堆拿走一些，或者从两堆中拿走一些．下面证明这三类都是胜态．
情况一：由命题一，任意一个比a[k+1]小的数都在之前的必败态中出现过，一旦把左边堆拿少了，我们只要再拿成那个数相应的必败态即可。
情况二（从右边堆拿走不太多）：这使得两堆之间的差变小了，比如拿成了(a[k+1],a[k+1]+m)，则可再拿成(a[m],a[m]+m)；
情况二（从右边堆拿走很多）：使得右边一堆比左边一堆更少，这时类似于情况一，比如拿成了(a[k+1],a[m])(其中a[m] 情况三：比如拿成(a[m],a[m]+k+1)，则可再拿成(a[m],a[m]+m)．
综上所述，任何从(a[k+1],a[k+1]+k+1)出发走向的状态都可以走回核中．故原命题成立．
以上两个命题对于确定(a[n],b[n])是完备的了，给定(0,0)然后按照这两个命题，就可以写出(1,2),(3,5),(4,7),…
这样我们得到了这个数列的递推式，以下我们把这两个命题当成是(a[n],b[n])的定义。
先证明两个性质：
性质一：核中的a[n],b[n]遍历所有正整数。
[分析]：由命题一，二可得a[n],b[n]是递增的，且由a[n]的定义显然。
性质二：A={a[n]:n=1,2,3,…},B={b[n]:n=1,2,3,…}，则集合A,B不交。
[分析]：由核是内固集，显然。
看到这里大家有没有想到Beatty序列呢，实际上a[n]和b[n]就是一个Beatty序列。
an=[αn],bn=[βn]，有 an+n=[(α+1)n]=[βn]，解方程 1/(α+1)+1/α=1
得 α=(sqrt5+1)/2，到此，我们找到了该必败态的通项公式。
实际上这组Beatty序列还有一些别的性质，比如当一个数是Fibonacci数的时候，另一个数也是Fibonacci数；而且两者的比值也越来越接近黄金比，这些性质在得到通项公式之后不难证明。
总的来说，这个问题给我们了哪些启示呢？首先用定理所说的方法找核，然后给出核的规律（递推，或是通项）并且证明。
方法二
定理 0：一个状态是必败态，当且仅当它的所有后继状态都是必胜态；而一个状态是必胜态，只要它的后继状态有一个以上的必败态即可。
证明略去。
容易发现下面的定理：
定理 1：(a，b) 和 (b, a) 的胜负性是相同的（a <> b）。
证明：如果 (a, b) 是必胜态，那么将必胜策略中所有的操作，对第一堆的变为第二堆，对第二堆的变为第一堆，就构成 (b, a) 的必胜策略
定理 2：若 (a, b) 是必败态，则对于所有的 x <> a 和 y <> b，(x, b) 和 (a, y) 是必胜态。
证明：
对于 x > a 和 y > b，不管是哪一种情况，总可以从 x 堆或 y 堆中取出一定量的石子使当前状态变为必败态 (a, b)，由定理 1，(x, b) 和 (a, y) 为必胜态。
对于 x < a 和 y < b，不管是哪一种情况，如果 (x, b) 或 (a, y) 是必败态的话，由上述可得 (a, b) 是必胜态，矛盾。故 (x, b) 和 (a, y) 均为为必胜态。
定理 3: 若 (a, b) 是必败态，则对于所有的 d > 0，(a + d, b + d) 是必胜态。
证明：
与定理 2 类似。
定理 4：在所有的必败态中，每个数字恰巧出现一次。
证明：
有了定理 1，对于对称的状态我们只需要处理其中一个，而两个数不会相同（相同的状态必然是必胜态），于是我们把每个状态中较小的数字放在前面，每行写一个状态，去掉括号并按照升序排列每行的第一个数，就构成了如下的矩阵：
1 2
3 5
4 7
6 10
……
假设数字k在矩阵中出现两次或两次以上，则有(k,a)，(k,b)都为必败态，与定理2矛盾。
假设数字k为序列中没有出现且值最小的数字，则有 (k,k+i)为必胜态(i>0)，则对任意i，必然存在j(0 根据鸽巢原理，必然存在3个i的取值(其实是无穷多个，j只有k-1种取值，而i有无数种)记为i1, i2, i3使得j1=j2=j3=m。对这3个i，同样必然存在一对i，不妨为(i1,i2)，使(k-m,k+i1-m)且(k-m,k+i2-m)必败或f(k-m,k+i1)且f(k-m,k+i2)必败。显然与定理2矛盾，因此不存在这样的数k。
观察这个矩阵，我们又可以得到新的定理：
定理 5：矩阵中每行第一个数恰巧是前面每一行中没有出现过的最小正整数。
证明：
由定理 4，矩阵中每个数字恰巧出现一次，而按照这个矩阵的定义，第二列的数总比同行第一列大，第一列又按照升序排列，所以每一行的第一个数正好为前面每一行中没有出现过的最小正整数。
定理 6：矩阵第 i 行的第二个数正好为第一个数加上 i
证明：
用数学归纳法。

1. 对于第一行显然成立
2. 若对于前 i - 1 行均成立，则所有的 (a[p], a[p] + p) (a[p] 为第 p 行第一个数，p < i) 均为必败态，那么考察第 i 行的状态 (a[i], a[i] + delta)。容易看出 delta >= i，因为如果 delta < i，一定可以通过一次操作变为前面出现过的必败态，那么这个状态就是必胜态。下面由 delta >= i，我们来说明 delta = i。
   首先，我们考虑从第一堆中取出 p 个石子，得到状态 (a[i] - p, a[i] - p + delta)，由定理 5，比 a[i] 小的数都在之前出现过，若 a[i] - p 出现在某一行的第一列，由于存在必败态 (a[i] - p, a[i] - p + d) (d < delta)，故 (a[i] - p, a[i] - p + delta) 一定为必胜态（定理 2）；若 a[i] - p 出现 在某一行的第二列，由于第一列是单增的，因而其对应的第一列数必小于 a[i] + delta，故而也可推出其状态为必胜态。
   对于从两堆石子中取出相同数目的情况与之类似，容易看出一定为必胜态。
   于是，(a[i], a[i] + delta) 状态的胜负性只与状态 (a[i], a[i] + d) (d < delta) 有关。不难看出，delta = i 时恰为必败态，因为不论从第二堆中取出多少个石子，作为另一堆的第一堆石子并没有在之前出现过，所以得到的一定是一个必胜态，因而 (a[i], a[i] + delta) 为必败态，由定理 2 及定理 4 可得，原命题成立。即矩阵中第 i 行第二列的数等于同行第一列的数加上 i。
   这时，我们所有的问题都转化到了矩阵上，只要能通过合适的方法表示出这个矩阵，我们就可以很好地解决原问题。
   下面的过程可能需要比较高的数学技巧，首先给出我们需要的一个重要定理（[x] 表示 x 的整数部分，{x} 表示 x 的小数部分，即 {x} = x - [x]）：
   定理 7（Betty 定理）：如果存在正无理数 A, B 满足 1/A + 1/B = 1，那么集合 P = { [At], t
   证明：Betty定理
   。
   考虑到 Betty 定理中“恰为 Z
   于是我们得到每一行第二列的数为 [
   我们的目的是要让 Z
   于是应用 Betty 定理，我们得到最终我们需要的定理：
   定理 8：上述矩阵中每一行第一列的数为 [
   证明：由 Betty 定理显然得证。
   设a、b是正无理数且 1/a +1/b =1。记P={ 【na】 | n为任意的正整数}，Q={ 【nb】 | n 为任意的正整数}，则P与Q是Z+的一个划分，即P∩Q为空集且P∪Q为正整数集合Z+。
   证明：因为a、b为正且1/a +1/b=1，则a、b>1，所以对于不同的整数n，【na】各不相同，类似对b有相同的结果。因此任一个整数至多在集合P或Q中出现一次。

• 现证明P∩Q为空集；(反证法)假设k为P∩Q的一个整数，则存在正整数m、n使得【ma】=【nb】=k。即k < ma、nb
• m/(k+1)< 1/a < m/k及n/(k+1)< 1/b < n/k。相加起来得 (m+n)/(k+1) < 1 < (m+n)/k，即 k < m+n < k+1。这与m、n为整数有矛盾，所以P∩Q为空集。现证明Z+=P∪Q；已知P∪Q是Z+的子集，剩下来只要证明Z+是P∪Q的子集。(反证法)假设Z+(P∪Q)有一个元素k，则存在正整数m、n使得【ma】< k <【(m+1)a】、【nb】< k <【(n+1)b】。 由此得ma < k ≦【 (m+1)a】-1<(m+1)a -1，类似地有nb < k ≦【 (n+1)b】-1<(n+1)b -1。等价地改写为 m/k < 1/a < (m+1)/(k+1)及n/k < 1/b < (n+1)/(k+1)。两式加起来，得
  (m+n)/k < 1 < (m+n+2)/(k+1)，即m+n < k < k+1 < m+n+2。这与m, n, k皆为正整数矛盾。所以Z+=P∪Q。
  结论：编辑
  两个人如果都采用正确操作，那么面对非奇异局势，先拿者必胜；反之，则后拿者取胜。
  那么任给一个局势（a，b），怎样判断它是不是奇异局势呢？我们有如下公式：
  ak =[k（1+√5）/2]，bk= ak + k （k=0，1，2，…n 方括号表示取整函数)
  奇妙的是其中出现了黄金分割数（1+√5）/2 = 1.618…因此，由ak，bk组成的矩形近似为黄金矩形，由于2/（1+√5）=（√5-1）/2，可以先求出j=[a（√5-1）/2]，若a=[j（1+√5）/2]，那么a = aj，bj = aj + j，若不等于，那么a = aj+1，b = aj + j + 1，若都不是，那么就不是奇异局势。然后再按照上述法则进行，一定会遇到奇异局势。
  题解代码
  说实话上述我看的一脸懵逼，慢慢想吧，这里直接上结论。。。

在这里插入代码片
#include
#include
int main()
{
    int t,n,m,temp;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        if(n>m)
        {
            int k=n;
            n=m;
            m=k;
        }
        temp=(m-n)*(sqrt(5)+1)/2;
        if(n==temp)
            printf("B\n");
        else
            printf("A\n");
    }
    return 0;
}