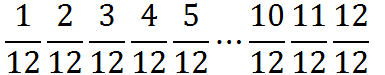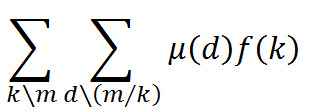在讲这个函数之前。最好先了解欧拉函数。
我们用 \ 记为整除。 记得小学的时候整除和整除以的概念么?别混淆。 2整除4 记作 2\4。
那么根据法里级数的展开(这个感觉和ACM关系不大就先不介绍了。大概讲的就是构造所有最简分数的一种树。而法里级数n定义分母<=n的最简分数。)
比如对于分母为12.
化简后:
分别为:
1/12 1/6 1/4 1/3 5/12 1/2 7/12 2/3 3/4 5/6 11/12 1/1
观察这些式子。你会发现分母都是能整除12的.也就是说分母为d。 d\m
分母为1的集合 1/1
分母为2的集合 1/2
分母为3的集合 1/3 2/3
分母为4的集合 1/4 3/4
分母为6的集合 1/6 5/6
分母为12的集合 1/12 5/12 7/12 11/12
会发现对于每个m的除数(也就是分母啦)的集合的分子都是和分母是互素的。并且穷举了。
比如4 1 和 3 是和4互素的。
1+1+2+2+2+4 = 12 (其实这里是废话!在推导中间就能得到了。因为我们列了12个分式嘛,重点在于是穷举了每个除数的互素数。)
不过我们可以从这得到一个和式:
重点在于这个形式的公式:
有一个结论:如果f(d) 让g(m)是积性函数。那么f(d) 是积性函数(这个结论很重要。)
同时如果我们能够证明这个结论的话。也可以通过这个结论去证明欧拉函数的积性。
因为根据上面我们推出的和式。对于欧拉函数的对应g(m)为m.m明显是积性的函数。
如果我们的结论成立。那么欧拉函数是积性的。(这里的积性不代表完全积性。我们知道欧拉函数的积性必须两个数互素的情况下才有。)
证明:
因为g(m)为积性函数,所以有:
扩展左边:
扩展右边:
即可得:
如果进一步细分左边和右边。会发现左边是
若该等式对于任意m恒成立.那么
根据上面的等式的话就是一个项一个项对应起来。而从这也能看出其逆命题也是正确的。就是当f(d) 为积性函数的时候 g(m)也为积性函数。
在此,欧拉函数的积性就算证明成功了。
对于上述的研究似乎没有提到莫比乌斯函数。但是以上的研究是贯彻整个莫比乌斯函数的。包括其积性的证明。和反演。
思考一个这样的问题:
欧拉函数是比较复杂的。而其对应的g(m) 是简单的。为m。
我们是否可以通过g(m)的函数能够获得f(m)的函数呢?(这里f(m)自变量变成m了。不过小小思考后明显不用在意。)
而我们有这样的一个反演原理:
莫比乌斯函数满足一个极其重要的性质。或者说是因为这个性质而定义了这个函数!
其中 [m=1]代表m=1的时候为1. m不等于1的时候为0
这个性质很神奇。但是却又不神奇。因为其实是认为构造出有这样的性质。使得莫比乌斯反演得以成立。
但是我们要计算其反演后的结果。我们又不得不知道具体的![]() 的值如何。其值我们先放着。先证明反演:
的值如何。其值我们先放着。先证明反演:
证明反演之前有两个步骤最好先需要有预备知识:
第一个:
这个其实思考一下就知道了。我们不过就是把计算顺序发生了改变。
第二个:
这个和式确实看起来复杂。而且我是直接搬其证明过程中遇到的这个和式。
不过我们从一个例子上去理解:
对于m = 12来说:
| d | 1 | 2 | 3 | 4 | 6 | 12 |
| m/d | 12 | 6 | 4 | 3 | 2 | 1 |
| k | 1 | 1 2 | 1 3 | 1 2 4 | 1 2 3 6 | 1 2 3 4 6 12 |
μ(12)f(1)
μ(6)f(1)+μ(6)f(2)
μ(4)f(1)+ μ(4)f(3)
μ(3)f(1)+μ(3)f(2)+ μ(3)f(4)
μ(2)f(1)+μ(2)f(2)+μ(2)f(3)+ μ(2)f(6)
μ(1)f(1)+μ(1)f(2)+μ(1)f(3)+μ(1)f(4)+μ(1)f(6)+μ(1)f(12)
+
-----------------------------------------------------------------------------
明显的求这个式子之和。
我们的排列是以μ的自变量排列的。那假如按f的自变量(k)进行排列呢? 我们上面的式子竖着都已经对应好了。
不难得出下表:(不根据式子。直接跟上)
| d | 12 | 12 6 | 12 4 | 12 6 3 | 12 6 4 2 | 12 6 4 2 1 |
| k | 12 | 6 | 4 | 3 | 2 | 1 |
| m/d | 1 | 1 2 | 1 3 | 1 2 4 | 1 2 3 6 | 1 2 3 4 6 12 |
细心对比上表:
| d | 1 | 2 | 3 | 4 | 6 | 12 |
| m/d | 12 | 6 | 4 | 3 | 2 | 1 |
| k | 1 | 1 2 | 1 3 | 1 2 4 | 1 2 3 6 | 1 2 3 4 6 12 |
会发现有意思的是m/d和k换了个位置而已。其实这并不是巧合。但是这并不是重点。
我们要用一个式子描述出这种情形。其实我们不过是把式子处理成以k为规整的。
而描述成和式其实就是上述恒等式的右边:
值得注意的是 d 已经不是原来的d了。只是一个从1开始的循环量而已。一旦满足d\(m/k) 就有意义。所以我本来第2个表不想统计d的。不过最后还是统计了。出于容易研究吧。
因为我们还得一点细节才能解释这个恒等式右边的表达式。
我们有:
k\d
d\m
所以对于指定的k,d的集合为k的倍数。
设l = m/d. (这里的l就是上述表达式的d!)
也就是我们要证明指定k 那么l的集合为 l\(m/k)
l = m/nk. n为整数。 (m/k) / l = n 所以l\(m/k).得证。
也许我的证明有点繁琐。如果你一眼看出来。那也没事。
其实就是寻找指定k m/d应该满足怎么样的条件。 其中k\d且d\m。
有了这2个恒等式我们可以接下来证明莫比乌斯反演:
证明过程:
PS:
其反证类似的。具体数学中的习题啊。也当作大家的习题好了。
就是第二个恒等式。具体数学中是分了2步。那个用拉斐尔证明的4.9虽然说原理并不难。但是具体数学上用得简直有点出神入化让我有点摸不着头脑。
之后一步是利用第一个恒等式然后证出上述的第二个恒等式。
首先:[m=1]这个函数是积性的。所以μ(d)这个函数必然也是积性的。利用我们一开始证明的那个结论。
也就是说要求μ(m).我们只要计算μ(p^k). 根据算术基本定理理所当然的。且p代表素数。
根据其性质:
m = p^k.
那么有 μ(1)+ μ(p^1) + μ(p^2) + μ(p^3)+...μ(p^k) = [p^k=1].
假如p = 1.(其实1不是素数,我们这样的假设是不成立的,这里只是为了运算出μ(1))
那么。 μ(1)= 1.
假如p != 1.
那么 μ(1)+ μ(p^1) + μ(p^2) + μ(p^3)+...μ(p^k) = 0.
当k=1.
μ(1)+ μ(p^1) = 0
可知μ(p^1)=μ(p)= -1.
当k=2.
μ(1)+ μ(p^1) + μ(p^2) = 0 .
即μ(p^2) = 0
同理。
μ(p^(3~k)) = 0
也就是说。
μ(1) = 1 , μ(p) = -1 , μ(p^k) = 0 (k>=2)
推广到 m:(m为任意实数)
下面0的情况。是存在p^2整除m.也就是m存在p^2因子的时候。
注意:μ(1) = 1
好了。反演和莫比乌斯的函数我们都理解透彻了。具体应用可以看这里