傅里叶变换一步步详细推导
前言
在本地Markdown下写的,传上来后公式不能对齐?
在大学的时候接触过几次傅里叶变换的知识,但是从来没真正懂过.也在网上找过很多资料,看过很多视频,但是,这些内容要么举些简单的例子说说直观上的理解,要么就是直接堆出公式没有任何推导.
直到一个巧合在B站上看到这样一个视频才真正搞懂,非常感谢这位UP主DR_CAN.这篇博客也主要是对视频中的推导模仿一遍.同时记录下笔记方便复习.
另外,记录当时一条印象很深的弹幕: 根本就没有人会学不懂数学,只是缺乏推导过程.
详细过程
1. 推导中的重要数学公式
三角函数系: { 1 , s i n ( x ) , c o s ( x ) , s i n ( 2 x ) , c o s ( 2 x ) , s i n ( 3 x ) , c o s ( 3 x ) , . . . , s i n ( n x ) , c o s ( n x ) } \{1,sin(x),cos(x),sin(2x),cos(2x),sin(3x),cos(3x),...,sin(nx),cos(nx)\} {1,sin(x),cos(x),sin(2x),cos(2x),sin(3x),cos(3x),...,sin(nx),cos(nx)}
在这个三角函数系里有个重要的性质,也就是傅里叶变换的推导精髓所在:
在三角函数系里任取两个不同的函数 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)(1也可以看作一个函数).都有一下公式成立:
∫ − π π f ( x ) g ( x ) d x = 0 \int_{-\pi}^{\pi}f(x)g(x)dx=0 ∫−ππf(x)g(x)dx=0
比如说: ∫ − π π s i n ( 4 x ) c o s ( 7 x ) d x = 0 \int_{-\pi}^{\pi}sin(4x)cos(7x)dx=0 ∫−ππsin(4x)cos(7x)dx=0, ∫ − π π 1 ⋅ s i n ( 9 x ) d x = 0 \int_{-\pi}^{\pi}1\cdot sin(9x)dx=0 ∫−ππ1⋅sin(9x)dx=0, ∫ − π π s i n ( x ) s i n ( x ) d x = 0 \int_{-\pi}^{\pi}sin(x)sin(x)dx=0 ∫−ππsin(x)sin(x)dx=0 , … …
如果取得 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)两个函数是相同的,那么
∫ − π π 1 ⋅ 1 d x = 2 π , ∫ − π π s i n ( n x ) s i n ( n x ) d x = π , ∫ − π π c o s ( n x ) c o s ( n x ) d x = π ( n = 1 , 2 , 3... ) \int_{-\pi}^{\pi}1 \cdot 1dx=2\pi,\int_{-\pi}^{\pi}sin(nx)sin(nx)dx=\pi,\int_{-\pi}^{\pi}cos(nx)cos(nx)dx=\pi \quad (n=1,2,3...) ∫−ππ1⋅1dx=2π,∫−ππsin(nx)sin(nx)dx=π,∫−ππcos(nx)cos(nx)dx=π(n=1,2,3...)
(这就不证明了,积分算一下就可以得到)
结论就是:任取三角函数系的不同函数相乘在一个周期的积分都为0.只有相同的函数才不为0.
欧拉公式:
e i θ = c o s ( θ ) + i s i n ( θ ) e^{i\theta}=cos(\theta)+isin(\theta) eiθ=cos(θ)+isin(θ)
简单地理解,欧拉公式就是复数的另一种表示形式. e i θ e^{i\theta} eiθ就看作复数.
2. 傅里叶级数
先讨论周期函数 f ( t ) f(t) f(t),周期为 T T T. 也就是 f ( t ) = f ( t + T ) f(t) = f(t+T) f(t)=f(t+T).
傅里叶级数本质就是用这无穷多个三角函数来表示或者无限近似函数 f ( t ) f(t) f(t).公式如下
f ( t ) = a 0 + ∑ n = 1 ∞ [ a n c o s ( n t ) + b n s i n ( n t ) ] f(t)=a_0+\sum_{n=1}^{\infty}[a_ncos(nt)+b_nsin(nt)] f(t)=a0+n=1∑∞[ancos(nt)+bnsin(nt)]
在上面的三角函数系里除了 1 , s i n ( x ) , c o s ( x ) 1,sin(x),cos(x) 1,sin(x),cos(x),其他函数其实都是在 s i n ( x ) , c o s ( x ) sin(x),cos(x) sin(x),cos(x)的乘上一个系数.这里 s i n ( x ) , c o s ( x ) sin(x),cos(x) sin(x),cos(x)的 T = 2 π 1 T=\frac{2\pi}{1} T=12π.我们令 w = 2 π T w=\frac{2\pi}{T} w=T2π. 称 w w w为基频率.在上面的三角函数系里基频率就是1.如果把最开始的 s i n ( x ) , c o s ( x ) sin(x),cos(x) sin(x),cos(x)换成 s i n ( 1.5 x ) , c o s ( 1.5 x ) sin(1.5x),cos(1.5x) sin(1.5x),cos(1.5x).那么整个三角函数系就变了啊.基频率也就变了.所以我们还需要一个变量 w w w来描述三角函数系长什么样子.上面公式没有 w w w只是因为碰巧 w = 1 w=1 w=1而已.所以傅里叶级数完整公式如下.(太啰嗦了… …)
f ( t ) = a 0 + ∑ n = 1 ∞ [ a n c o s ( n w t ) + b n s i n ( n w t ) ] f(t)=a_0+\sum_{n=1}^{\infty}[a_ncos(nwt)+b_nsin(nwt)] f(t)=a0+n=1∑∞[ancos(nwt)+bnsin(nwt)]
写到这里其实就差不多了,但是欧拉说这里我必须要插一脚.这个公式太难看了.
根据欧拉公式有
e i n w t = c o s ( n w t ) + i s i n ( n w t ) e − i n w t = c o s ( n w t ) − i s i n ( n w t ) e^{inwt}=cos(nwt)+isin(nwt) \\ e^{-inwt}=cos(nwt)-isin(nwt) einwt=cos(nwt)+isin(nwt)e−inwt=cos(nwt)−isin(nwt)
那么
c o s ( n w t ) = e i n w t + e − i n w t 2 , s i n ( n w t ) = e i n w t − e − i n w t 2 i cos(nwt)=\frac{e^{inwt}+e^{-inwt}}{2},sin(nwt)=\frac{e^{inwt}-e^{-inwt}}{2i} cos(nwt)=2einwt+e−inwt,sin(nwt)=2ieinwt−e−inwt
带入上式
f ( t ) = a 0 + ∑ n = 1 ∞ [ a n e i n w t + e − i n w t 2 + b n e i n w t − e − i n w t 2 i ] f ( t ) = a 0 + ∑ n = 1 ∞ ( a n − i b n 2 ) e i n w t + ∑ n = 1 ∞ ( a n + i b n 2 ) e − i n w t f(t)=a_0+\sum_{n=1}^{\infty}[a_n\frac{e^{inwt}+e^{-inwt}}{2}+b_n\frac{e^{inwt}-e^{-inwt}}{2i}] \\ f(t)=a_0+\sum_{n=1}^{\infty}(\frac{a_n-ib_n}{2})e^{inwt}+\sum_{n=1}^{\infty}(\frac{a_n+ib_n}{2})e^{-inwt} f(t)=a0+n=1∑∞[an2einwt+e−inwt+bn2ieinwt−e−inwt]f(t)=a0+n=1∑∞(2an−ibn)einwt+n=1∑∞(2an+ibn)e−inwt
还不够好看啊,好像也不能再化简了吧.(但是接下来这个操作很帅,注意细节)
f ( t ) = ∑ n = 0 0 a n e i n w t + ∑ n = 1 ∞ ( a n − i b n 2 ) e i n w t + ∑ n = − 1 − ∞ ( a − n + i b − n 2 ) e i n w t f ( t ) = ∑ n = − ∞ ∞ c n e i n w t f(t)=\sum_{n=0}^{0}a_ne^{inwt}+\sum_{n=1}^{\infty}(\frac{a_n-ib_n}{2})e^{inwt}+\sum_{n=-1}^{-\infty}(\frac{a_{-n}+ib_{-n}}{2})e^{inwt} \\ f(t)=\sum_{n=-\infty}^{\infty} c_ne^{inwt} f(t)=n=0∑0aneinwt+n=1∑∞(2an−ibn)einwt+n=−1∑−∞(2a−n+ib−n)einwtf(t)=n=−∞∑∞cneinwt
其中
当 n = 0 时 , c n = a 0 当 n = 1 , 2 , 3... 时 , c n = a n − i b n 2 当 n = − 1 , − 2 , − 3... 时 , c n = a − n + i b − n 2 当n=0时,c_n=a_0 \\ 当n=1,2,3...时,c_n=\frac{a_n-ib_n}{2}\\ 当n=-1,-2,-3...时,c_n=\frac{a_{-n}+ib_{-n}}{2} 当n=0时,cn=a0当n=1,2,3...时,cn=2an−ibn当n=−1,−2,−3...时,cn=2a−n+ib−n
虽然很简洁,但是本质上都是一样的,只是公式的恒等变形.?
3. 周期函数傅里叶变换
分析上面的公式, t t t是变量,其实sin,cos里面都是固定的.不知道的只有 a 0 , a n , b n a_0,a_n,b_n a0,an,bn.如果知道了 a 0 , a n , b n a_0,a_n,b_n a0,an,bn,那函数 f ( t ) f(t) f(t)就写成了三角函数之和的形式了.下面就来求 a 0 , a n , b n a_0,a_n,b_n a0,an,bn.
先求 a 0 a_0 a0,对上式左右两边同时乘上 1 1 1,也就是同时乘上 c o s ( 0 t ) cos(0t) cos(0t),再从 0 0 0到 T T T积分
∫ 0 T f ( t ) d t = ∫ 0 T a 0 d t + ∫ 0 T ∑ n = 1 ∞ [ a n c o s ( n w t ) + b n s i n ( n w t ) ] d t ∫ 0 T f ( t ) c o s ( 0 t ) d t = ∫ 0 T a 0 c o s ( 0 t ) d t + ∫ 0 T ∑ n = 1 ∞ [ a n c o s ( n w t ) c o s ( 0 t ) + b n s i n ( n w t ) c o s ( 0 t ) ] d t \int_0^T f(t)dt=\int_0^T a_0dt+ \int_0^T \sum_{n=1}^{\infty}[a_ncos(nwt)+b_nsin(nwt)]dt \\ \int_0^T f(t)cos(0t)dt=\int_0^T a_0cos(0t)dt+ \int_0^T \sum_{n=1}^{\infty}[a_ncos(nwt)cos(0t)+b_nsin(nwt)cos(0t)]dt ∫0Tf(t)dt=∫0Ta0dt+∫0Tn=1∑∞[ancos(nwt)+bnsin(nwt)]dt∫0Tf(t)cos(0t)dt=∫0Ta0cos(0t)dt+∫0Tn=1∑∞[ancos(nwt)cos(0t)+bnsin(nwt)cos(0t)]dt
写到这里应该就可以知道三角函数系的结论能干什么了吧?
上式最右边那项里面 c o s ( n w t ) c o s ( 0 t ) cos(nwt)cos(0t) cos(nwt)cos(0t),对它积分不就等于0嘛. s i n ( n w t ) c o s ( 0 t ) sin(nwt)cos(0t) sin(nwt)cos(0t),对它积分也等于0.因为他们在三角函数系是不同的函数啊.因此
∫ 0 T f ( t ) d t = ∫ 0 T a 0 c o s ( 0 t ) d t + 0 ∫ 0 T f ( t ) d t = ∫ 0 T a 0 d t = T ⋅ a 0 a 0 = 1 T ∫ 0 T f ( t ) d t \int_0^T f(t)dt=\int_0^T a_0cos(0t)dt+0 \\ \int_0^T f(t)dt=\int_0^T a_0dt =T \cdot a_0\\ a_0=\frac{1}{T}\int_0^T f(t)dt ∫0Tf(t)dt=∫0Ta0cos(0t)dt+0∫0Tf(t)dt=∫0Ta0dt=T⋅a0a0=T1∫0Tf(t)dt
接着算 a n a_n an,这里 n = 1 , 2 , 3... n=1,2,3... n=1,2,3... 对傅里叶级数公式左右两边同时乘上 c o s ( m w t ) cos(mwt) cos(mwt),再从 0 0 0到 T T T积分
f ( t ) = a 0 + ∑ n = 1 ∞ [ a n c o s ( n w t ) + b n s i n ( n w t ) ] ∫ 0 T f ( t ) c o s ( m w t ) d t = ∫ 0 T a 0 c o s ( m w t ) d t + ∫ 0 T c o s ( m w t ) ∑ n = 1 ∞ [ a n c o s ( n w t ) + b n s i n ( n w t ) ] d t ∫ 0 T f ( t ) c o s ( m w t ) d t = ∫ 0 T a 0 c o s ( 0 t ) c o s ( m w t ) d t + ∫ 0 T c o s ( m w t ) ∑ n = 1 ∞ [ a n c o s ( n w t ) + b n s i n ( n w t ) ] d t f(t)=a_0+\sum_{n=1}^{\infty}[a_ncos(nwt)+b_nsin(nwt)] \\ \int_0^T f(t)cos(mwt)dt=\int_0^T a_0cos(mwt)dt+ \int_0^T cos(mwt)\sum_{n=1}^{\infty}[a_ncos(nwt)+b_nsin(nwt)]dt \\ \int_0^T f(t)cos(mwt)dt=\int_0^T a_0cos(0t)cos(mwt)dt+ \int_0^T cos(mwt)\sum_{n=1}^{\infty}[a_ncos(nwt)+b_nsin(nwt)]dt f(t)=a0+n=1∑∞[ancos(nwt)+bnsin(nwt)]∫0Tf(t)cos(mwt)dt=∫0Ta0cos(mwt)dt+∫0Tcos(mwt)n=1∑∞[ancos(nwt)+bnsin(nwt)]dt∫0Tf(t)cos(mwt)dt=∫0Ta0cos(0t)cos(mwt)dt+∫0Tcos(mwt)n=1∑∞[ancos(nwt)+bnsin(nwt)]dt
看到了吧,三角函数系的结论又来了,对 c o s ( 0 t ) c o s ( m w t ) , s i n ( n w t ) c o s ( m w t ) cos(0t)cos(mwt),sin(nwt)cos(mwt) cos(0t)cos(mwt),sin(nwt)cos(mwt)的积分又都是0了.只有 c o s ( n w t ) c o s ( n w t ) cos(nwt)cos(nwt) cos(nwt)cos(nwt)的积分才不等于0,对于其他 m ≠ n , c o s ( m w t ) c o s ( n w t ) m \ne n,cos(mwt)cos(nwt) m=n,cos(mwt)cos(nwt)的积分也是0,因此求和符号也就没了
∫ 0 T f ( t ) c o s ( m w t ) d t = 0 + ∫ 0 T ∑ n = 1 ∞ a n c o s ( n w t ) c o s ( m w t ) d t + ∫ 0 T ∑ n = 1 ∞ b n s i n ( n w t ) c o s ( m w t ) d t ∫ 0 T f ( t ) c o s ( m w t ) d t = ∫ 0 T a m c o s ( m w t ) c o s ( m w t ) d t + 0 ∫ 0 T f ( t ) c o s ( m w t ) d t = ∫ 0 T a m c o s 2 ( m w t ) d t = a m ∫ 0 T 1 + c o s ( 2 m w t ) 2 d t = T 2 a m a m = 2 T ∫ 0 T f ( t ) c o s ( m w t ) d t ( m = 1 , 2 , 3... ) a n = 2 T ∫ 0 T f ( t ) c o s ( n w t ) d t ( n = 1 , 2 , 3... ) \int_0^T f(t)cos(mwt)dt=0+ \int_0^T \sum_{n=1}^{\infty}a_ncos(nwt)cos(mwt)dt+\int_0^T \sum_{n=1}^{\infty}b_nsin(nwt)cos(mwt)dt \\ \int_0^T f(t)cos(mwt)dt=\int_0^T a_mcos(mwt)cos(mwt)dt+0 \\ \int_0^T f(t)cos(mwt)dt=\int_0^T a_mcos^2(mwt)dt=a_m\int_0^T \frac{1+cos(2mwt)}{2}dt= \frac{T}{2}a_m \\ a_m = \frac{2}{T}\int_0^T f(t)cos(mwt)dt \quad (m=1,2,3...) \\ a_n = \frac{2}{T}\int_0^T f(t)cos(nwt)dt \quad (n=1,2,3...) ∫0Tf(t)cos(mwt)dt=0+∫0Tn=1∑∞ancos(nwt)cos(mwt)dt+∫0Tn=1∑∞bnsin(nwt)cos(mwt)dt∫0Tf(t)cos(mwt)dt=∫0Tamcos(mwt)cos(mwt)dt+0∫0Tf(t)cos(mwt)dt=∫0Tamcos2(mwt)dt=am∫0T21+cos(2mwt)dt=2Tamam=T2∫0Tf(t)cos(mwt)dt(m=1,2,3...)an=T2∫0Tf(t)cos(nwt)dt(n=1,2,3...)
求得了 a n a_n an,来算 b n b_n bn. 其实很明显能观察到的相似性,我们根据 a n a_n an的规律直接得出 b n b_n bn
b n = 2 T ∫ 0 T f ( t ) s i n ( n w t ) d t ( n = 1 , 2 , 3... ) b_n = \frac{2}{T}\int_0^T f(t)sin(nwt)dt \quad (n=1,2,3...) bn=T2∫0Tf(t)sin(nwt)dt(n=1,2,3...)
现在把 a 0 , a n , b n a_0,a_n,b_n a0,an,bn,带入上面求 c n c_n cn的公式
当 n = 0 n=0 n=0时
c n = a 0 = 1 T ∫ 0 T f ( t ) d t = 1 T ∫ 0 T f ( t ) e − i w ⋅ 0 d t c_n=a_0=\frac{1}{T}\int_0^T f(t)dt=\frac{1}{T}\int_0^T f(t)e^{-iw \cdot 0}dt cn=a0=T1∫0Tf(t)dt=T1∫0Tf(t)e−iw⋅0dt
当 n = 1 , 2 , 3... n=1,2,3... n=1,2,3...时
c n = a n − i b n 2 = 2 T ∫ 0 T f ( t ) c o s ( n w t ) d t − i ⋅ 2 T ∫ 0 T f ( t ) s i n ( n w t ) d t 2 = 1 T ∫ 0 T f ( t ) [ c o s ( n w t ) − i s i n ( n w t ) ] d t = 1 T ∫ 0 T f ( t ) e − i n w t d t c_n=\frac{a_n-ib_n}{2} = \frac{\frac{2}{T}\int_0^T f(t)cos(nwt)dt-i\cdot\frac{2}{T}\int_0^T f(t)sin(nwt)dt }{2} \\ =\frac{1}{T}\int_0^{T}f(t)[cos(nwt)-isin(nwt)]dt \\ =\frac{1}{T}\int_0^{T}f(t)e^{-inwt}dt cn=2an−ibn=2T2∫0Tf(t)cos(nwt)dt−i⋅T2∫0Tf(t)sin(nwt)dt=T1∫0Tf(t)[cos(nwt)−isin(nwt)]dt=T1∫0Tf(t)e−inwtdt
当 n = − 1 , − 2 , − 3... n=-1,-2,-3... n=−1,−2,−3...时
c n = a − n + i b − n 2 = 2 T ∫ 0 T f ( t ) c o s ( − n w t ) d t + i ⋅ 2 T ∫ 0 T f ( t ) s i n ( − n w t ) d t 2 = 1 T ∫ 0 T f ( t ) [ c o s ( n w t ) − i s i n ( n w t ) ] d t = 1 T ∫ 0 T f ( t ) e − i n w t d t c_n=\frac{a_{-n}+ib_{-n}}{2} = \frac{\frac{2}{T}\int_0^T f(t)cos(-nwt)dt+i\cdot\frac{2}{T}\int_0^T f(t)sin(-nwt)dt }{2} \\ =\frac{1}{T}\int_0^{T}f(t)[cos(nwt)-isin(nwt)]dt \\ =\frac{1}{T}\int_0^{T}f(t)e^{-inwt}dt cn=2a−n+ib−n=2T2∫0Tf(t)cos(−nwt)dt+i⋅T2∫0Tf(t)sin(−nwt)dt=T1∫0Tf(t)[cos(nwt)−isin(nwt)]dt=T1∫0Tf(t)e−inwtdt
我们惊奇地发现对于任意整数 n n n, c n c_n cn的表达式都是一样的.?
总结上面的公式
f ( t ) = ∑ n = − ∞ ∞ c n e i n w t 其 中 , c n = 1 T ∫ 0 T f ( t ) e − i n w t d t f(t)=\sum_{n=-\infty}^{\infty} c_ne^{inwt} \quad 其中,c_n=\frac{1}{T}\int_0^{T}f(t)e^{-inwt}dt f(t)=n=−∞∑∞cneinwt其中,cn=T1∫0Tf(t)e−inwtdt
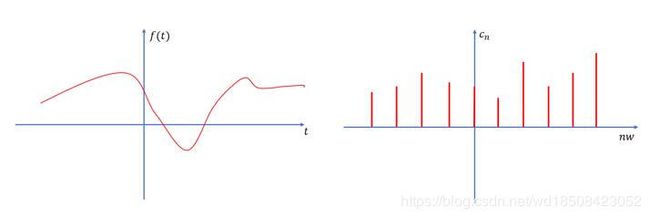
其中 c n c_n cn是可以通过上面公式算出来的复数.而 e e e的指数 i n w t inwt inwt,对于每一个不同的函数 f ( t ) f(t) f(t)其实都是一样的.那么决定函数的不同其实就是 c n c_n cn.我们知道一系列这样的 ( t , f ( t ) ) (t,f(t)) (t,f(t))对就可以画出函数图像,也就是说这样的 ( t , f ( t ) ) (t,f(t)) (t,f(t))能够唯一确定函数.但是现在我们的函数由这样的 ( n , c n ) (n,c_n) (n,cn)对来确定了.其实也就是说函数表示发生了转化–从时域到频域的转化.函数值是不变的,它们等号连接的嘛.只是表诉的方式改变了.如下图
(上图右边纵轴 c n c_n cn其实是个复数,可以理解为应该有两个维度,一个实部,一个虚部,但是这里为了简单画图,就把它画成了实数.但其实它是个复数.)
4. 任意函数傅里叶变换
对于一个非周期函数,我们可以假设它是个周期函数,它的周期 T → + ∞ T \to + \infty T→+∞.就可以用上面的公式求出了.
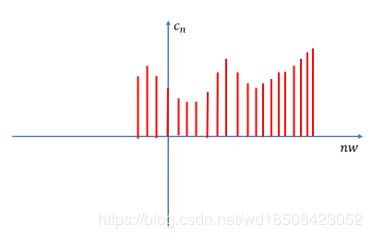
w w w是基频率. w = 2 π T w=\frac{2\pi}{T} w=T2π.当 T → + ∞ T \to + \infty T→+∞时, w → 0 w\to 0 w→0. w = ( n + 1 ) w − n w = Δ w w=(n+1)w-nw=\Delta w w=(n+1)w−nw=Δw.所以 Δ w → 0 \Delta w \to 0 Δw→0.
从上图可以看到,随着 Δ w → 0 \Delta w \to 0 Δw→0, n w nw nw会从一个离散的量变为一个连续的变量.
对于上小节中 c n c_n cn可以写作
c n = 1 T ∫ − T 2 − T 2 f ( t ) e − i n w t d t c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{-\frac{T}{2}}f(t)e^{-inwt}dt cn=T1∫−2T−2Tf(t)e−inwtdt
那么,对于任意函数的变换为
f ( t ) = lim T → ∞ ∑ n = − ∞ ∞ 1 T ∫ − T 2 − T 2 f ( t ) e − i n w t d t e i n w t = lim Δ w → 0 ∑ n = − ∞ ∞ Δ w 2 π ∫ − ∞ + ∞ f ( t ) e − i n w t d t e i n w t f(t) = \lim_{T\to \infty}\sum_{n=-\infty}^{\infty} \frac{1}{T}\int_{-\frac{T}{2}}^{-\frac{T}{2}}f(t)e^{-inwt}dt\ e^{inwt} \\ = \lim_{\Delta w \to 0}\sum_{n=-\infty}^{\infty}\frac{\Delta w}{2\pi}\int_{-\infty}^{+\infty}f(t)e^{-inwt}dt\ e^{inwt} f(t)=T→∞limn=−∞∑∞T1∫−2T−2Tf(t)e−inwtdt einwt=Δw→0limn=−∞∑∞2πΔw∫−∞+∞f(t)e−inwtdt einwt
当 Δ w → 0 \Delta w\to 0 Δw→0时, ( n + 1 ) w (n+1)w (n+1)w和 n w nw nw就几乎相等.令 W = n w W=nw W=nw,( w w w是一经确定就不变的量, n n n才是离散的变量),那么就可以把 W W W看作连续变化的量.所以上式求和就可写作求积分
f ( t ) = ∫ − ∞ + ∞ 1 2 π ( ∫ − ∞ + ∞ f ( t ) e − i W t d t ) e i W t d W = 1 2 π ∫ − ∞ + ∞ ( ∫ − ∞ + ∞ f ( t ) e − i W t d t ) e i W t d W f(t) = \int_{-\infty}^{+\infty}\frac{1}{2\pi}(\int_{-\infty}^{+\infty}f(t)e^{-iWt}dt)\ e^{iWt} dW \\ =\frac{1}{2\pi}\int_{-\infty}^{+\infty}(\int_{-\infty}^{+\infty}f(t)e^{-iWt}dt)\ e^{iWt} dW f(t)=∫−∞+∞2π1(∫−∞+∞f(t)e−iWtdt) eiWtdW=2π1∫−∞+∞(∫−∞+∞f(t)e−iWtdt) eiWtdW
其中, ∫ − ∞ + ∞ f ( t ) e − i W t d t \int_{-\infty}^{+\infty}f(t)e^{-iWt}dt ∫−∞+∞f(t)e−iWtdt的积分变量是 t t t,也就是说它是关于 W W W的函数.令
F ( W ) = ∫ − ∞ + ∞ f ( t ) e − i W t d t F(W) =\int_{-\infty}^{+\infty}f(t)e^{-iWt}dt F(W)=∫−∞+∞f(t)e−iWtdt
那么函数 F ( W ) F(W) F(W)就是 f ( t ) f(t) f(t)的傅里叶变换.把 F ( W ) F(W) F(W)带入 f ( t ) f(t) f(t)得
f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( W ) e i W t d W f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(W)\ e^{iWt} dW f(t)=2π1∫−∞+∞F(W) eiWtdW
f ( t ) f(t) f(t)就是傅里叶变换的逆变换.
函数.令
F ( W ) = ∫ − ∞ + ∞ f ( t ) e − i W t d t F(W) =\int_{-\infty}^{+\infty}f(t)e^{-iWt}dt F(W)=∫−∞+∞f(t)e−iWtdt
那么函数 F ( W ) F(W) F(W)就是 f ( t ) f(t) f(t)的傅里叶变换.把 F ( W ) F(W) F(W)带入 f ( t ) f(t) f(t)得
f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( W ) e i W t d W f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(W)\ e^{iWt} dW f(t)=2π1∫−∞+∞F(W) eiWtdW
f ( t ) f(t) f(t)就是傅里叶变换的逆变换.