【模式识别与机器学习】贝叶斯公式

1 贝叶斯公式

设x是个随机变量，表示为鱼的光泽度，w1、w2分别表示鲈鱼和鲑鱼。已知的先验概率为p(w1)+p(w2) = 1。

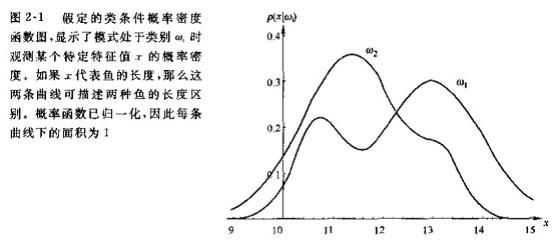
P(x | w) 表示类别状态为w时的x的概率密度函数，有时也称为状态条件概率密度。因此，p(x | w1)与p(x | w2)之间的区别就表示了鲈鱼与鲑鱼间光泽度的区别。如图2.1

在通过观察和测量（这在实际应用中，可以通过训练语料的出），发现了一条鱼的光泽度x，及其所属的类别w。类别w，并且具有特征值x的模式的联合概率密度可以写成：

p(w,x) = p(w|x)p(x) = p(x|w)p(w)。 公式1

公式1通过，以下公式推导出来。p(x|w)=p(x,w)/p(w), p(w|x)=p(w,x)/p(x), p(w,x)=p(x,w)。

从而，推出公式1。

从上述公式可以得出，p(w|x) = (p(x|w)p(w))/p(x) 公式2

公式2成为贝叶斯公式。

贝叶斯公式可用非正式的英语表示成：posterior = (likelihood * prior) / evidence.

通过观测x的值，我们可以将先验概率p(w)转换为后验概率p(w|x)，即假设特征x已知的条件下类别属于w的概率。

称p(x | w)为w关于x的似然函数，或简称为“似然”（likelihood），表明在其他条件都相等的情况下，是的p(x|w)较大的w更具有可能是真实的类别。

注意，后验概率主要是由先验概率和似然函数的乘积所决定的，证据因子(evidence)p(x)可仅仅看成是一个标量因子，以保证各类别的后验概率综合为1。

后验概率图，如2.2

从上图，可以看出如果一个观测值x，使得p(w1|x)比p(w2|x)大，我们很自然的会做出真实类别是w1的判决。

判决的误差率为：p(error|x) = {p(w1|x) 如果判为w2, p(w2|x) 如果判为w1}。