同余问题（3）一元线性同余方程组

简单的一元线性同余方程组：

对于一元线性方程组：

······

解决的思路是两两不断合并，逐个破解：

进一步写成：

相关解决过程：

cin>>a1>>r1;
bool judge=1;
for(int i=1;i<n;i++){
   cin>>a2>>r2;
   int d,x0,y0;
   int c=r2-r1;
   exgcd(a1,a2,d,x0,y0);  //d =gcd(a1,a2);
    if(c%d!=0)   judge=0;
    int  t=a2/d;
    x0=(x0*(c/d)%t+t)%t;   // *
    r1=a1*x0+r1;  //所求x
    a1=a1*(a2/d);  //a_1变为a_1,a_2的最小公倍数
}
if(judge==0)  r1=-1;
return r1;

关于 * 的解释：  

应用：http://acm.hdu.edu.cn/showproblem.php?pid=3579
分析：即求解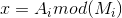 样式的方程组，找到最小的x。（注意0的情况）

#include <iostream>  
#include <cstdio>  
using namespace std;  
int A[10],M[10],n,lcm;  
int gcd(int a,int b){  
    return b==0?a:gcd(b,a%b);  
}  
void exgcd(int a,int b,int &d,int &x,int &y){  
     if(b==0){  
        x=1;  y=0;  d=a;  
        return ;  
     }  
     exgcd(b,a%b,d,y,x);  
     y-=x*(a/b);  
}  
int main()  
{  
    int t,ca=1;  
    cin>>t;  
    while(t--){  
        scanf("%d",&n);  
        scanf("%d",&M[0]);  
        lcm=M[0];  
        for(int i=1;i<n;i++){  
            scanf("%d",&M[i]);  
            lcm=M[i]/gcd(lcm,M[i])*lcm;  
        }  
        for(int i=0;i<n;i++){  
            scanf("%d",&A[i]);  
        }  
        printf("Case %d: ",ca++);  
        int a1=M[0],r1=A[0],a2,r2;  
        bool judge=1;  
        for(int i=1;i<n;i++){  
            a2=M[i];  
            r2=A[i];  
            int d,x0,y0,c=r2-r1;  
            exgcd(a1,a2,d,x0,y0);  
            if(c%d!=0){  
                judge=0;  
                break;  
            }  
            int  t=a2/d;  
            x0=(x0*(c/d)%t+t)%t;  
            r1=a1*x0+r1;  //所求x  
            a1=a1*(a2/d);  
        }  
        if(judge==0) r1=-1;  
        if(r1==0) printf("%d\n",lcm);  
        else printf("%d\n",r1);  
    }  
    return 0;  
}  

问题： http://poj.org/problem?id=2891
pku 2891 Strange Way to Express Integers（线性同余方程）
大意：问题就是求解m，满足n个方程：
也即是

#include <iostream>  
#include <cstdio>  
using namespace std;  
typedef long long LL;  
void exgcd(LL a,LL b,LL &d,LL &x,LL &y){  
    if(b==0) {  
        d=a;  x=1;  y=0;  
        return ;  
    }  
    exgcd(b,a%b,d,y,x);  
    y=y-(a/b)*x;  
}  
int main()  
{  
    //freopen("cin.txt","r",stdin);  
    LL n;  
    while(cin>>n){  
        LL r1,a1,r2,a2;  
        bool has=1;  
        scanf("%lld%lld",&a1,&r1);  
        for(int i=1;i<n;i++){  
            scanf("%lld%lld",&a2,&r2);  
            LL a=a1,b=a2,c=r2-r1,d,x,y;  
            exgcd(a,b,d,x,y);  
            if(c%d!=0) has=0;  
            int t=b/d;  
            x=(x*(c/d)%t+t)%t;  
            r1=x*a1+r1;  
            a1=a1*(a2/d);  
        }  
        if(!has) puts("-1");  
        else  printf("%lld\n",r1);  
    }  
    return 0;  
}  

对于更普遍的方程组问题，可以求出a的逆元将之转化成，这样就能变成上面的求解思路了。